Variance Reduction for Inverse Trace Estimation via Random Spanning Forests

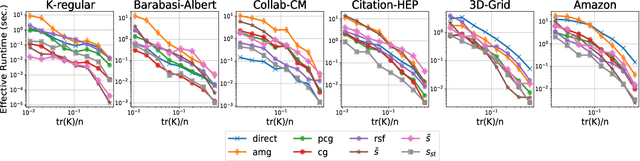
The trace $\tr(q(\ma{L} + q\ma{I})^{-1})$, where $\ma{L}$ is a symmetric diagonally dominant matrix, is the quantity of interest in some machine learning problems. However, its direct computation is impractical if the matrix size is large. State-of-the-art methods include Hutchinson's estimator combined with iterative solvers, as well as the estimator based on random spanning forests (a random process on graphs). In this work, we show two ways of improving the forest-based estimator via well-known variance reduction techniques, namely control variates and stratified sampling. Implementing these techniques is easy, and provides substantial variance reduction, yielding comparable or better performance relative to state-of-the-art algorithms.

Optimized Algorithms to Sample Determinantal Point Processes

In this technical report, we discuss several sampling algorithms for Determinantal Point Processes (DPP). DPPs have recently gained a broad interest in the machine learning and statistics literature as random point processes with negative correlation, i.e., ones that can generate a "diverse" sample from a set of items. They are parametrized by a matrix $\mathbf{L}$, called $L$-ensemble, that encodes the correlations between items. The standard sampling algorithm is separated in three phases: 1/~eigendecomposition of $\mathbf{L}$, 2/~an eigenvector sampling phase where $\mathbf{L}$'s eigenvectors are sampled independently via a Bernoulli variable parametrized by their associated eigenvalue, 3/~a Gram-Schmidt-type orthogonalisation procedure of the sampled eigenvectors. In a naive implementation, the computational cost of the third step is on average $\mathcal{O}(N\mu^3)$ where $\mu$ is the average number of samples of the DPP. We give an algorithm which runs in $\mathcal{O}(N\mu^2)$ and is extremely simple to implement. If memory is a constraint, we also describe a dual variant with reduced memory costs. In addition, we discuss implementation details often missing in the literature.

Échantillonnage de signaux sur graphes via des processus déterminantaux

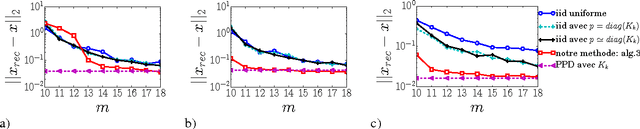
We consider the problem of sampling k-bandlimited graph signals, ie, linear combinations of the first k graph Fourier modes. We know that a set of k nodes embedding all k-bandlimited signals always exists, thereby enabling their perfect reconstruction after sampling. Unfortunately, to exhibit such a set, one needs to partially diagonalize the graph Laplacian, which becomes prohibitive at large scale. We propose a novel strategy based on determinantal point processes that side-steps partial diagonalisation and enables reconstruction with only O(k) samples. While doing so, we exhibit a new general algorithm to sample determinantal process, faster than the state-of-the-art algorithm by an order k.

Visualizing the Effects of a Changing Distance on Data Using Continuous Embeddings

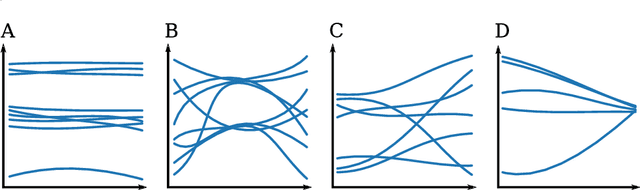
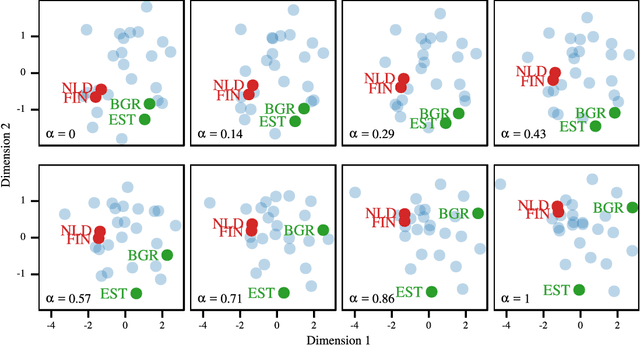
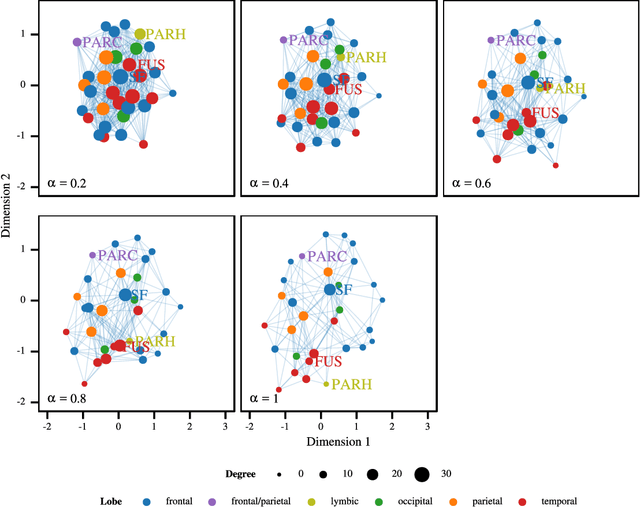
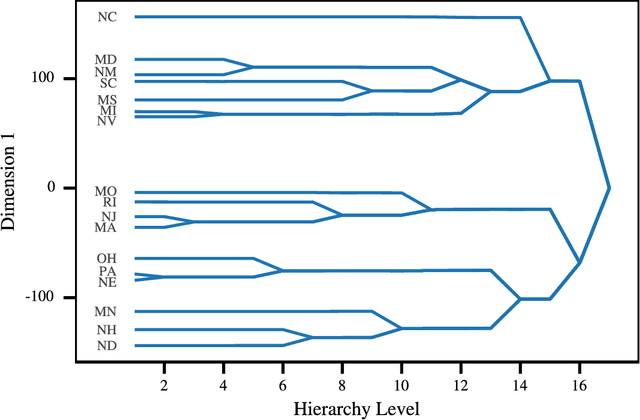
Most Machine Learning (ML) methods, from clustering to classification, rely on a distance function to describe relationships between datapoints. For complex datasets it is hard to avoid making some arbitrary choices when defining a distance function. To compare images, one must choose a spatial scale, for signals, a temporal scale. The right scale is hard to pin down and it is preferable when results do not depend too tightly on the exact value one picked. Topological data analysis seeks to address this issue by focusing on the notion of neighbourhood instead of distance. It is shown that in some cases a simpler solution is available. It can be checked how strongly distance relationships depend on a hyperparameter using dimensionality reduction. A variant of dynamical multi-dimensional scaling (MDS) is formulated, which embeds datapoints as curves. The resulting algorithm is based on the Concave-Convex Procedure (CCCP) and provides a simple and efficient way of visualizing changes and invariances in distance patterns as a hyperparameter is varied. A variant to analyze the dependence on multiple hyperparameters is also presented. A cMDS algorithm that is straightforward to implement, use and extend is provided. To illustrate the possibilities of cMDS, cMDS is applied to several real-world data sets.