Variance Reduction for Inverse Trace Estimation via Random Spanning Forests
Paper and Code
Jun 15, 2022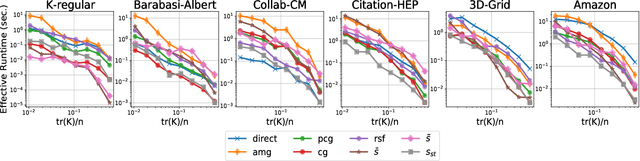
The trace $\tr(q(\ma{L} + q\ma{I})^{-1})$, where $\ma{L}$ is a symmetric diagonally dominant matrix, is the quantity of interest in some machine learning problems. However, its direct computation is impractical if the matrix size is large. State-of-the-art methods include Hutchinson's estimator combined with iterative solvers, as well as the estimator based on random spanning forests (a random process on graphs). In this work, we show two ways of improving the forest-based estimator via well-known variance reduction techniques, namely control variates and stratified sampling. Implementing these techniques is easy, and provides substantial variance reduction, yielding comparable or better performance relative to state-of-the-art algorithms.
* GRETSI 22, Sep 2022, Nancy, France
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge