Determinantal Point Processes for Coresets

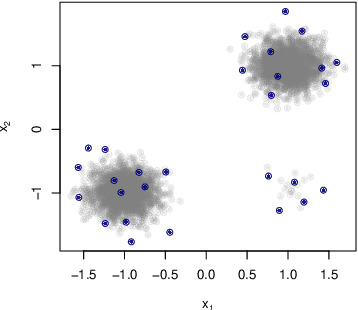
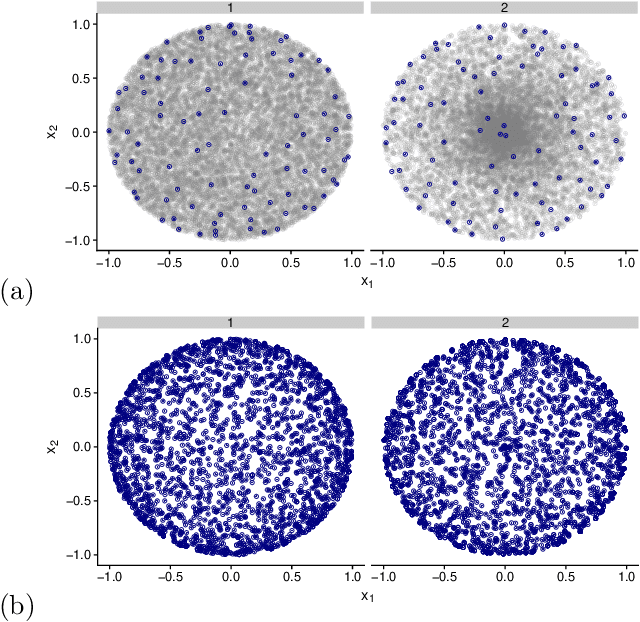
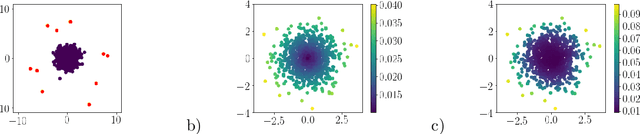
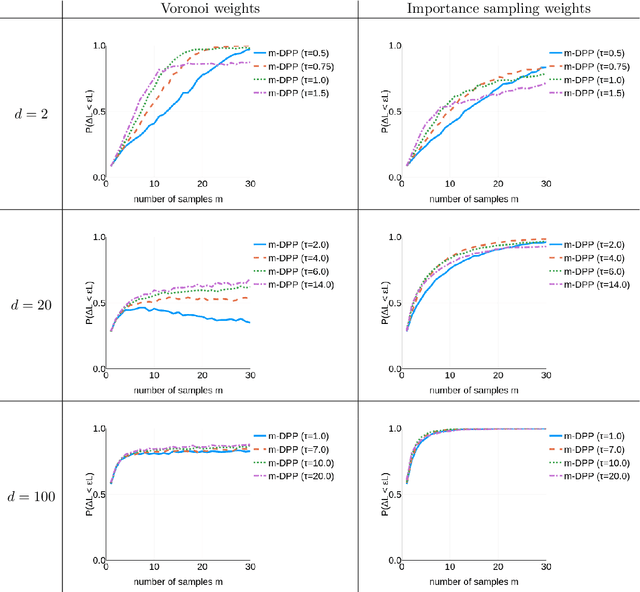
When one is faced with a dataset too large to be used all at once, an obvious solution is to retain only part of it. In practice this takes a wide variety of different forms, but among them "coresets" are especially appealing. A coreset is a (small) weighted sample of the original data that comes with a guarantee: that a cost function can be evaluated on the smaller set instead of the larger one, with low relative error. For some classes of problems, and via a careful choice of sampling distribution, iid random sampling has turned to be one of the most successful methods to build coresets efficiently. However, independent samples are sometimes overly redundant, and one could hope that enforcing diversity would lead to better performance. The difficulty lies in proving coreset properties in non-iid samples. We show that the coreset property holds for samples formed with determinantal point processes (DPP). DPPs are interesting because they are a rare example of repulsive point processes with tractable theoretical properties, enabling us to construct general coreset theorems. We apply our results to the $k$-means problem, and give empirical evidence of the superior performance of DPP samples over state of the art methods.