Caract{é}risation d'une Source Diffuse {à} partir des Moments de sa Densit{é} de Puissance en Tomographie SAR

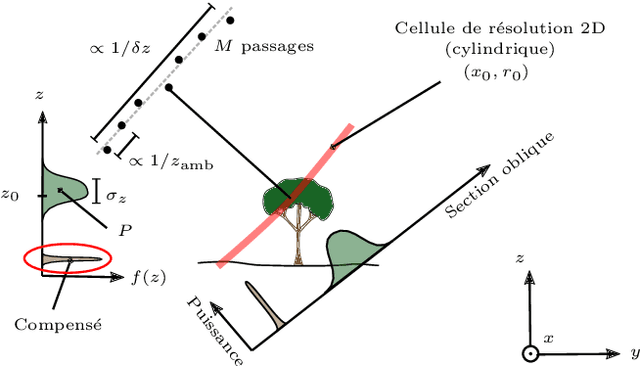
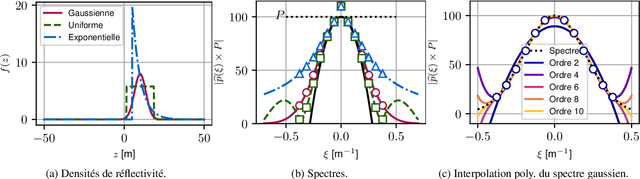
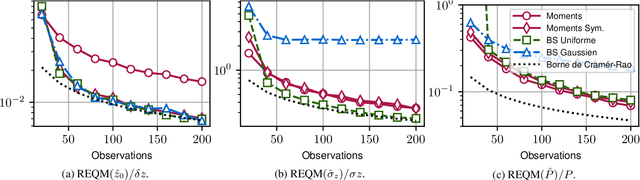
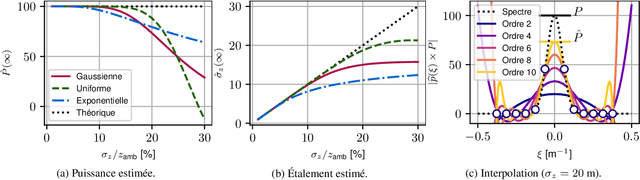
This paper presents a method for estimating the characteristics of a diffuse source from interferometric measurements in the context of SAR tomography. The proposed method is based on the use of central moments of the reflectivity density and does not use any a priori model. The method's performance is discussed as a function of antenna array parameters (resolution and ambiguity).

Moment-based Characterization of Spatially Distributed Sources in SAR Tomography

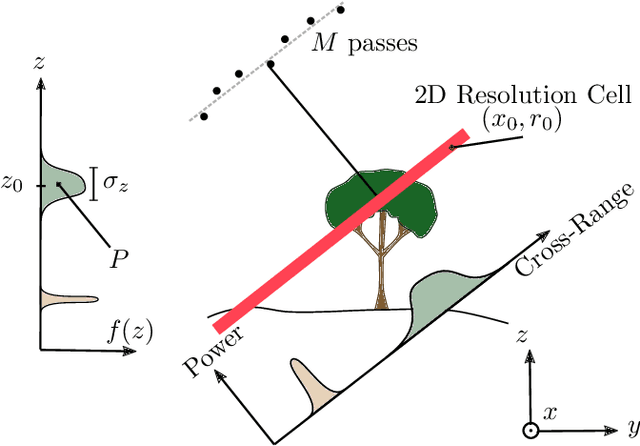
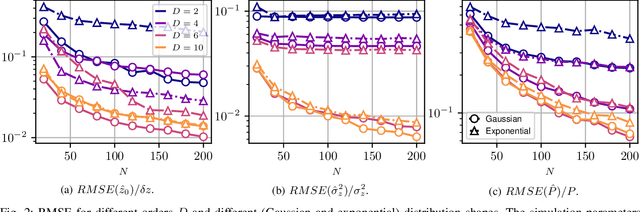
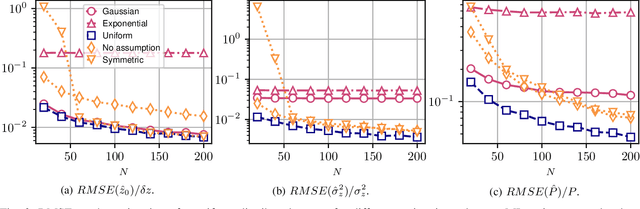
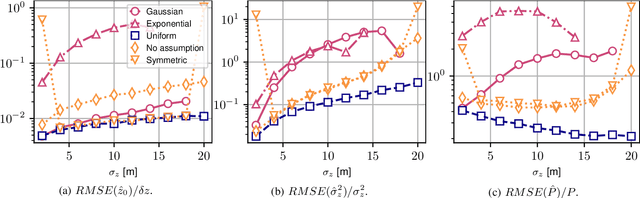
This paper presents a non-parametric method for 3-D imaging of natural volumes using Synthetic Aperture Radar tomography. This array processing-based technique aims at characterizing a spatially distributed density of incoherent sources, whose shape is imprecisely known. The proposed technique estimates the moments of the reflectivity density using a low-complexity covariance matching approach, and retrieves the mean location, dispersion, and power of the distributed source. Numerical simulations of realistic tomographic scenarios show that the proposed model-free scheme achieves better accuracy than slightly misspecified maximum likelihood estimators, derived from approximately known distribution shapes.

Revisiting Split Covariance Intersection: Correlated Components and Optimality

Linear fusion is a cornerstone of estimation theory. Implementing optimal linear fusion requires knowledge of the covariance of the vector of errors associated with all the estimators. In distributed or cooperative systems, the cross-covariance terms cannot be computed, and to avoid underestimating the estimation error, conservative fusions must be performed. A conservative fusion provides a fused estimator with a covariance bound that is guaranteed to be larger than the true, but computationally intractable, covariance of the error. Previous research by Reinhardt \textit{et al.} proved that, if no additional assumption is made about the errors of the estimators, the minimal bound for fusing two estimators is given by a fusion called Covariance Intersection (CI). In distributed systems, the estimation errors contain independent and correlated terms induced by the measurement noises and the process noise. In this case, CI is no longer the optimal method. Split Covariance Intersection (SCI) has been developed to take advantage of the uncorrelated components. This paper extends SCI to also take advantage of the correlated components. Then, it is proved that the new fusion provides the optimal conservative fusion bounds for two estimators, generalizing the optimality of CI to a wider class of fusion schemes. The benefits of this extension are demonstrated in simulations.

Split Covariance Intersection with Correlated Components for Distributed Estimation

This paper introduces a new conservative fusion method to exploit the correlated components within the estimation errors. Fusion is the process of combining multiple estimates of a given state to produce a new estimate with a smaller MSE. To perform the optimal linear fusion, the (centralized) covariance associated with the errors of all estimates is required. If it is partially unknown, the optimal fusion cannot be computed. Instead, a solution is to perform a conservative fusion. A conservative fusion provides a gain and a bound on the resulting MSE matrix which guarantees that the error is not underestimated. A well-known conservative fusion is the Covariance Intersection fusion. It has been modified to exploit the uncorrelated components within the errors. In this paper, it is further extended to exploit the correlated components as well. The resulting fusion is integrated into standard distributed algorithms where it allows exploiting the process noise observed by all agents. The improvement is confirmed by simulations.

Pseudorange Rigidity and Solvability of Cooperative GNSS Positioning

Global Navigation Satellite Systems (GNSS) are a widely used technology for positioning and navigation. GNSS positioning relies on pseudorange measurements from satellites to receivers. A pseudorange is the apparent distance between two agents deduced from the time-of-flight of a signal sent from one agent to the other. Because of the lack of synchronization between the agents' clocks, it is a biased version of their distance. This paper introduces a new rigidity theory adapted to pseudorange measurements. The peculiarity of pseudoranges is that they are asymmetrical measurements. Therefore, unlike other usual rigidities, the graphs of pseudorange frameworks are directed. In this paper, pseudorange rigidity is proved to be a generic property of the underlying undirected graph of constraints. The main result is a characterization of rigid pseudorange graphs as combinations of rigid distance graphs and connected graphs. This new theory is adapted for GNSS. It provides new insights into the minimum number of satellites needed to locate a receiver, and is applied to the localization of GNSS cooperative networks of receivers. The interests of asymmetrical constraints in the context of formation control are also discussed.

Fusion of Distance Measurements between Agents with Unknown Correlations

Cooperative localization is a promising solution to improve the accuracy and overcome the shortcomings of GNSS. Cooperation is often achieved by measuring the distance between users. To optimally integrate a distance measurement between two users into a navigation filter, the correlation between the errors of their estimates must be known. Unfortunately, in large scale networks the agents cannot compute these correlations and must use consistent filters. A consistent filter provides an upper bound on the covariance of the error of the estimator taking into account all the possible correlations. In this paper, a consistent linear filter for integrating a distance measurement is derived using Split Covariance Intersection. Its analysis shows that a distance measurement between two agents can only benefit one of them, i.e., only one of the two can use the distance measurement to improve its estimator. Furthermore, in some cases, none can. A necessary condition for an agent to benefit from the measurement is given for a general class of objective functions. When the objective function is the trace or the determinant, necessary and sufficient conditions are given.