The Poisson transform for unnormalised statistical models
Paper and Code
Nov 27, 2014
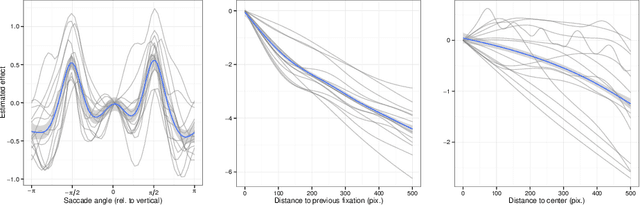
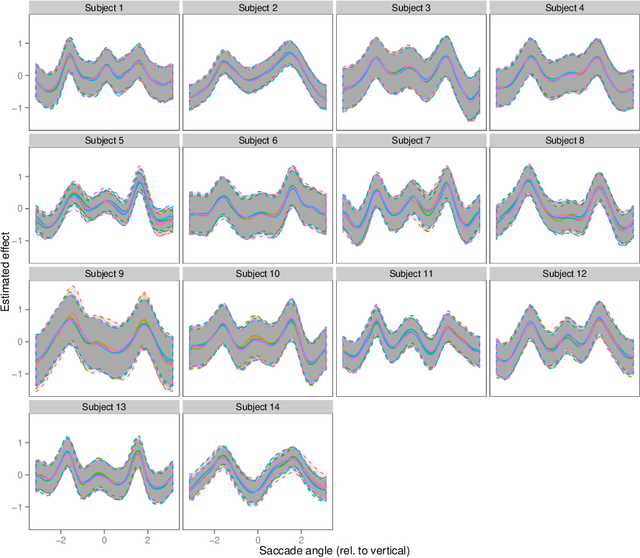
Contrary to standard statistical models, unnormalised statistical models only specify the likelihood function up to a constant. While such models are natural and popular, the lack of normalisation makes inference much more difficult. Here we show that inferring the parameters of a unnormalised model on a space $\Omega$ can be mapped onto an equivalent problem of estimating the intensity of a Poisson point process on $\Omega$. The unnormalised statistical model now specifies an intensity function that does not need to be normalised. Effectively, the normalisation constant may now be inferred as just another parameter, at no loss of information. The result can be extended to cover non-IID models, which includes for example unnormalised models for sequences of graphs (dynamical graphs), or for sequences of binary vectors. As a consequence, we prove that unnormalised parameteric inference in non-IID models can be turned into a semi-parametric estimation problem. Moreover, we show that the noise-contrastive divergence of Gutmann & Hyv\"arinen (2012) can be understood as an approximation of the Poisson transform, and extended to non-IID settings. We use our results to fit spatial Markov chain models of eye movements, where the Poisson transform allows us to turn a highly non-standard model into vanilla semi-parametric logistic regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge