Dynamic angular synchronization under smoothness constraints

Given an undirected measurement graph $\mathcal{H} = ([n], \mathcal{E})$, the classical angular synchronization problem consists of recovering unknown angles $\theta_1^*,\dots,\theta_n^*$ from a collection of noisy pairwise measurements of the form $(\theta_i^* - \theta_j^*) \mod 2\pi$, for all $\{i,j\} \in \mathcal{E}$. This problem arises in a variety of applications, including computer vision, time synchronization of distributed networks, and ranking from pairwise comparisons. In this paper, we consider a dynamic version of this problem where the angles, and also the measurement graphs evolve over $T$ time points. Assuming a smoothness condition on the evolution of the latent angles, we derive three algorithms for joint estimation of the angles over all time points. Moreover, for one of the algorithms, we establish non-asymptotic recovery guarantees for the mean-squared error (MSE) under different statistical models. In particular, we show that the MSE converges to zero as $T$ increases under milder conditions than in the static setting. This includes the setting where the measurement graphs are highly sparse and disconnected, and also when the measurement noise is large and can potentially increase with $T$. We complement our theoretical results with experiments on synthetic data.

Dynamic Ranking and Translation Synchronization

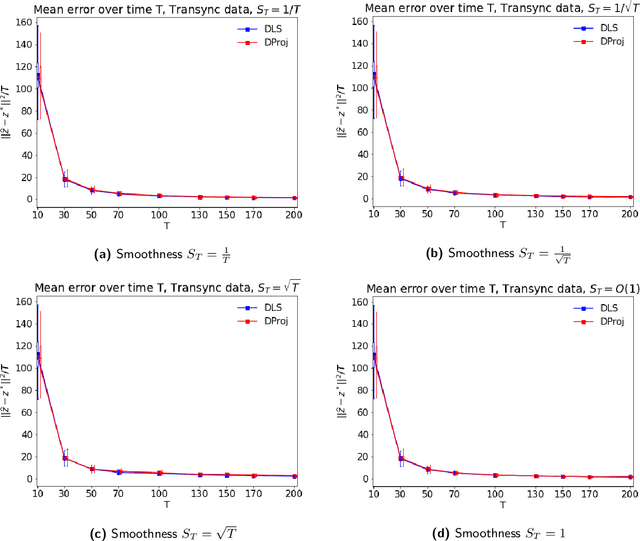
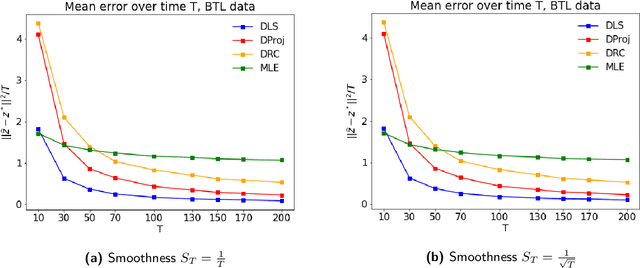
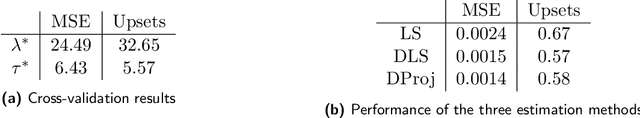
In many applications, such as sport tournaments or recommendation systems, we have at our disposal data consisting of pairwise comparisons between a set of $n$ items (or players). The objective is to use this data to infer the latent strength of each item and/or their ranking. Existing results for this problem predominantly focus on the setting consisting of a single comparison graph $G$. However, there exist scenarios (e.g., sports tournaments) where the the pairwise comparison data evolves with time. Theoretical results for this dynamic setting are relatively limited and is the focus of this paper. We study an extension of the \emph{translation synchronization} problem, to the dynamic setting. In this setup, we are given a sequence of comparison graphs $(G_t)_{t\in \mathcal{T}}$, where $\mathcal{T} \subset [0,1]$ is a grid representing the time domain, and for each item $i$ and time $t\in \mathcal{T}$ there is an associated unknown strength parameter $z^*_{t,i}\in \mathbb{R}$. We aim to recover, for $t\in\mathcal{T}$, the strength vector $z^*_t=(z^*_{t,1},\dots,z^*_{t,n})$ from noisy measurements of $z^*_{t,i}-z^*_{t,j}$, where $\{i,j\}$ is an edge in $G_t$. Assuming that $z^*_t$ evolves smoothly in $t$, we propose two estimators -- one based on a smoothness-penalized least squares approach and the other based on projection onto the low frequency eigenspace of a suitable smoothness operator. For both estimators, we provide finite sample bounds for the $\ell_2$ estimation error under the assumption that $G_t$ is connected for all $t\in \mathcal{T}$, thus proving the consistency of the proposed methods in terms of the grid size $|\mathcal{T}|$. We complement our theoretical findings with experiments on synthetic and real data.

Seeded graph matching for the correlated Wigner model via the projected power method

In the graph matching problem we observe two graphs $G,H$ and the goal is to find an assignment (or matching) between their vertices such that some measure of edge agreement is maximized. We assume in this work that the observed pair $G,H$ has been drawn from the correlated Wigner model -- a popular model for correlated weighted graphs -- where the entries of the adjacency matrices of $G$ and $H$ are independent Gaussians and each edge of $G$ is correlated with one edge of $H$ (determined by the unknown matching) with the edge correlation described by a parameter $\sigma\in [0,1)$. In this paper, we analyse the performance of the projected power method (PPM) as a seeded graph matching algorithm where we are given an initial partially correct matching (called the seed) as side information. We prove that if the seed is close enough to the ground-truth matching, then with high probability, PPM iteratively improves the seed and recovers the ground-truth matching (either partially or exactly) in $\mathcal{O}(\log n)$ iterations. Our results prove that PPM works even in regimes of constant $\sigma$, thus extending the analysis in (Mao et al.,2021) for the sparse Erd\"os-Renyi model to the (dense) Wigner model. As a byproduct of our analysis, we see that the PPM framework generalizes some of the state-of-art algorithms for seeded graph matching. We support and complement our theoretical findings with numerical experiments on synthetic data.

Latent Distance Estimation for Random Geometric Graphs

Random geometric graphs are a popular choice for a latent points generative model for networks. Their definition is based on a sample of $n$ points $X_1,X_2,\cdots,X_n$ on the Euclidean sphere~$\mathbb{S}^{d-1}$ which represents the latent positions of nodes of the network. The connection probabilities between the nodes are determined by an unknown function (referred to as the "link" function) evaluated at the distance between the latent points. We introduce a spectral estimator of the pairwise distance between latent points and we prove that its rate of convergence is the same as the nonparametric estimation of a function on $\mathbb{S}^{d-1}$, up to a logarithmic factor. In addition, we provide an efficient spectral algorithm to compute this estimator without any knowledge on the nonparametric link function. As a byproduct, our method can also consistently estimate the dimension $d$ of the latent space.