The Price of Robustness: Stable Classifiers Need Overparameterization

The relationship between overparameterization, stability, and generalization remains incompletely understood in the setting of discontinuous classifiers. We address this gap by establishing a generalization bound for finite function classes that improves inversely with class stability, defined as the expected distance to the decision boundary in the input domain (margin). Interpreting class stability as a quantifiable notion of robustness, we derive as a corollary a law of robustness for classification that extends the results of Bubeck and Sellke beyond smoothness assumptions to discontinuous functions. In particular, any interpolating model with $p \approx n$ parameters on $n$ data points must be unstable, implying that substantial overparameterization is necessary to achieve high stability. We obtain analogous results for parameterized infinite function classes by analyzing a stronger robustness measure derived from the margin in the codomain, which we refer to as the normalized co-stability. Experiments support our theory: stability increases with model size and correlates with test performance, while traditional norm-based measures remain largely uninformative.

Time to Spike? Understanding the Representational Power of Spiking Neural Networks in Discrete Time

Recent years have seen significant progress in developing spiking neural networks (SNNs) as a potential solution to the energy challenges posed by conventional artificial neural networks (ANNs). However, our theoretical understanding of SNNs remains relatively limited compared to the ever-growing body of literature on ANNs. In this paper, we study a discrete-time model of SNNs based on leaky integrate-and-fire (LIF) neurons, referred to as discrete-time LIF-SNNs, a widely used framework that still lacks solid theoretical foundations. We demonstrate that discrete-time LIF-SNNs with static inputs and outputs realize piecewise constant functions defined on polyhedral regions, and more importantly, we quantify the network size required to approximate continuous functions. Moreover, we investigate the impact of latency (number of time steps) and depth (number of layers) on the complexity of the input space partitioning induced by discrete-time LIF-SNNs. Our analysis highlights the importance of latency and contrasts these networks with ANNs employing piecewise linear activation functions. Finally, we present numerical experiments to support our theoretical findings.

Sustainable AI: Mathematical Foundations of Spiking Neural Networks

Deep learning's success comes with growing energy demands, raising concerns about the long-term sustainability of the field. Spiking neural networks, inspired by biological neurons, offer a promising alternative with potential computational and energy-efficiency gains. This article examines the computational properties of spiking networks through the lens of learning theory, focusing on expressivity, training, and generalization, as well as energy-efficient implementations while comparing them to artificial neural networks. By categorizing spiking models based on time representation and information encoding, we highlight their strengths, challenges, and potential as an alternative computational paradigm.

Computability of Classification and Deep Learning: From Theoretical Limits to Practical Feasibility through Quantization

The unwavering success of deep learning in the past decade led to the increasing prevalence of deep learning methods in various application fields. However, the downsides of deep learning, most prominently its lack of trustworthiness, may not be compatible with safety-critical or high-responsibility applications requiring stricter performance guarantees. Recently, several instances of deep learning applications have been shown to be subject to theoretical limitations of computability, undermining the feasibility of performance guarantees when employed on real-world computers. We extend the findings by studying computability in the deep learning framework from two perspectives: From an application viewpoint in the context of classification problems and a general limitation viewpoint in the context of training neural networks. In particular, we show restrictions on the algorithmic solvability of classification problems that also render the algorithmic detection of failure in computations in a general setting infeasible. Subsequently, we prove algorithmic limitations in training deep neural networks even in cases where the underlying problem is well-behaved. Finally, we end with a positive observation, showing that in quantized versions of classification and deep network training, computability restrictions do not arise or can be overcome to a certain degree.

Mathematical Algorithm Design for Deep Learning under Societal and Judicial Constraints: The Algorithmic Transparency Requirement

Deep learning still has drawbacks in terms of trustworthiness, which describes a comprehensible, fair, safe, and reliable method. To mitigate the potential risk of AI, clear obligations associated to trustworthiness have been proposed via regulatory guidelines, e.g., in the European AI Act. Therefore, a central question is to what extent trustworthy deep learning can be realized. Establishing the described properties constituting trustworthiness requires that the factors influencing an algorithmic computation can be retraced, i.e., the algorithmic implementation is transparent. Motivated by the observation that the current evolution of deep learning models necessitates a change in computing technology, we derive a mathematical framework which enables us to analyze whether a transparent implementation in a computing model is feasible. We exemplarily apply our trustworthiness framework to analyze deep learning approaches for inverse problems in digital and analog computing models represented by Turing and Blum-Shub-Smale Machines, respectively. Based on previous results, we find that Blum-Shub-Smale Machines have the potential to establish trustworthy solvers for inverse problems under fairly general conditions, whereas Turing machines cannot guarantee trustworthiness to the same degree.

Expressivity of Spiking Neural Networks

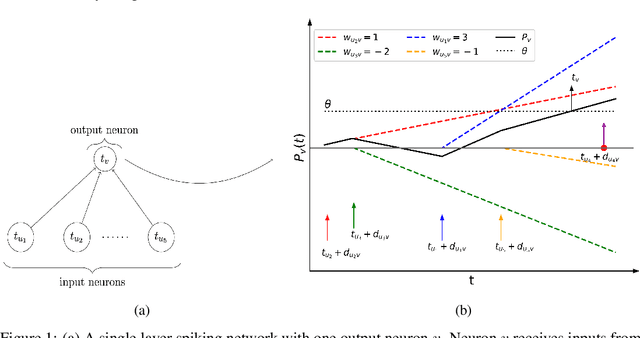
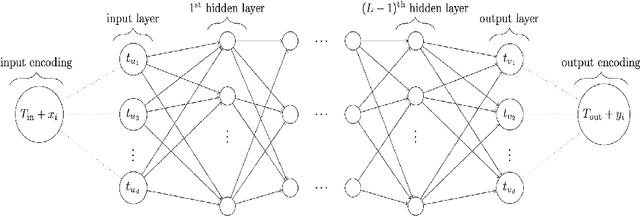
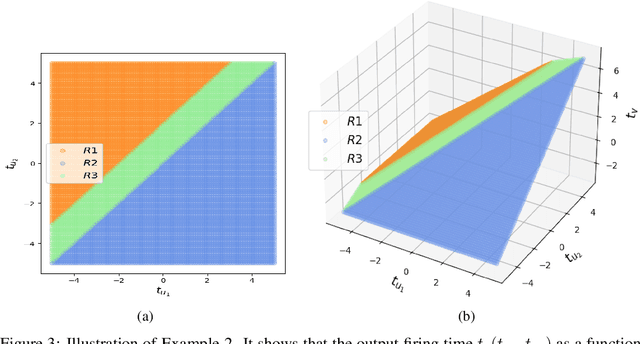
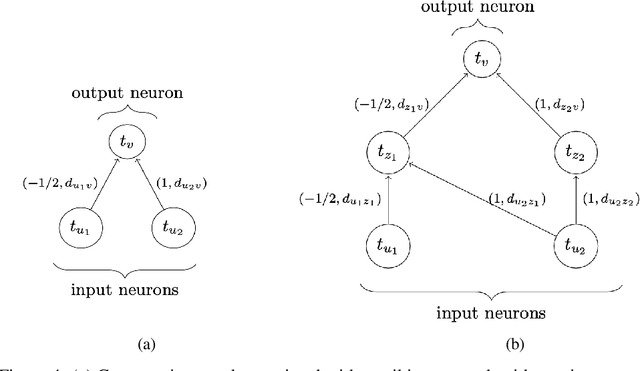
This article studies the expressive power of spiking neural networks where information is encoded in the firing time of neurons. The implementation of spiking neural networks on neuromorphic hardware presents a promising choice for future energy-efficient AI applications. However, there exist very few results that compare the computational power of spiking neurons to arbitrary threshold circuits and sigmoidal neurons. Additionally, it has also been shown that a network of spiking neurons is capable of approximating any continuous function. By using the Spike Response Model as a mathematical model of a spiking neuron and assuming a linear response function, we prove that the mapping generated by a network of spiking neurons is continuous piecewise linear. We also show that a spiking neural network can emulate the output of any multi-layer (ReLU) neural network. Furthermore, we show that the maximum number of linear regions generated by a spiking neuron scales exponentially with respect to the input dimension, a characteristic that distinguishes it significantly from an artificial (ReLU) neuron. Our results further extend the understanding of the approximation properties of spiking neural networks and open up new avenues where spiking neural networks can be deployed instead of artificial neural networks without any performance loss.

Inverse Problems Are Solvable on Real Number Signal Processing Hardware

Inverse problems are used to model numerous tasks in imaging sciences, in particular, they encompass any task to reconstruct data from measurements. Thus, the algorithmic solvability of inverse problems is of significant importance. The study of this question is inherently related to the underlying computing model and hardware, since the admissible operations of any implemented algorithm are defined by the computing model and the hardware. Turing machines provide the fundamental model of today's digital computers. However, it has been shown that Turing machines are incapable of solving finite dimensional inverse problems for any given accuracy. This stimulates the question of how powerful the computing model must be to enable the general solution of finite dimensional inverse problems. This paper investigates the general computation framework of Blum-Shub-Smale (BSS) machines which allows the processing and storage of arbitrary real values. Although a corresponding real world computing device does not exist at the moment, research and development towards real number computing hardware, usually referred to by the term "neuromorphic computing", has increased in recent years. In this work, we show that real number computing in the framework of BSS machines does enable the algorithmic solvability of finite dimensional inverse problems. Our results emphasize the influence of the considered computing model in questions of algorithmic solvability of inverse problems.

Limitations of Deep Learning for Inverse Problems on Digital Hardware

Deep neural networks have seen tremendous success over the last years. Since the training is performed on digital hardware, in this paper, we analyze what actually can be computed on current hardware platforms modeled as Turing machines, which would lead to inherent restrictions of deep learning. For this, we focus on the class of inverse problems, which, in particular, encompasses any task to reconstruct data from measurements. We prove that finite-dimensional inverse problems are not Banach-Mazur computable for small relaxation parameters. In fact, our result even holds for Borel-Turing computability., i.e., there does not exist an algorithm which performs the training of a neural network on digital hardware for any given accuracy. This establishes a conceptual barrier on the capabilities of neural networks for finite-dimensional inverse problems given that the computations are performed on digital hardware.