Expressivity of Spiking Neural Networks
Paper and Code
Aug 16, 2023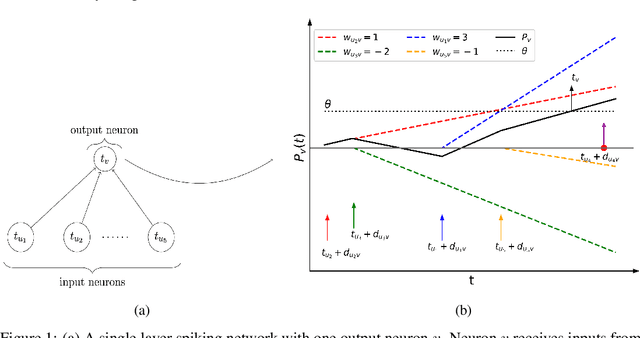
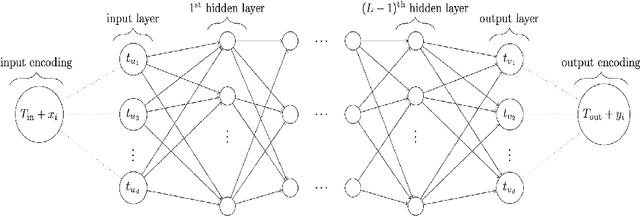
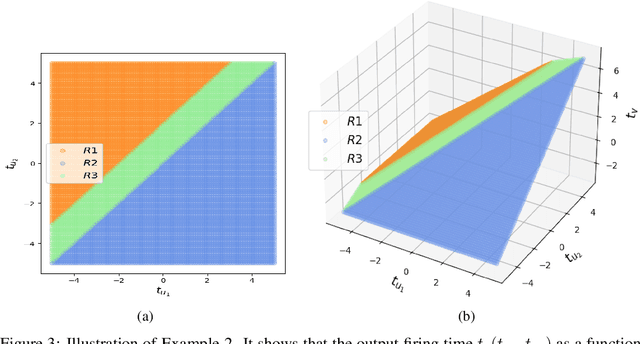
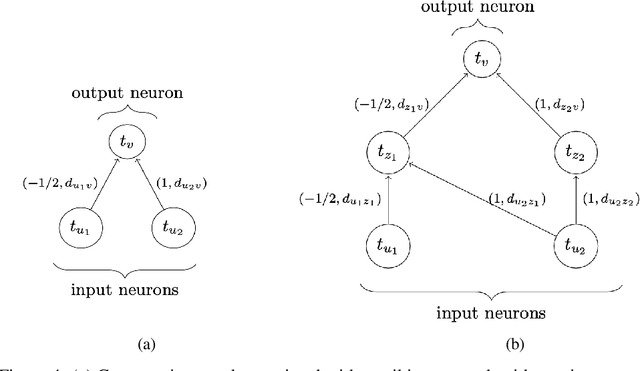
This article studies the expressive power of spiking neural networks where information is encoded in the firing time of neurons. The implementation of spiking neural networks on neuromorphic hardware presents a promising choice for future energy-efficient AI applications. However, there exist very few results that compare the computational power of spiking neurons to arbitrary threshold circuits and sigmoidal neurons. Additionally, it has also been shown that a network of spiking neurons is capable of approximating any continuous function. By using the Spike Response Model as a mathematical model of a spiking neuron and assuming a linear response function, we prove that the mapping generated by a network of spiking neurons is continuous piecewise linear. We also show that a spiking neural network can emulate the output of any multi-layer (ReLU) neural network. Furthermore, we show that the maximum number of linear regions generated by a spiking neuron scales exponentially with respect to the input dimension, a characteristic that distinguishes it significantly from an artificial (ReLU) neuron. Our results further extend the understanding of the approximation properties of spiking neural networks and open up new avenues where spiking neural networks can be deployed instead of artificial neural networks without any performance loss.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge