DRAW2ACT: Turning Depth-Encoded Trajectories into Robotic Demonstration Videos

Video diffusion models provide powerful real-world simulators for embodied AI but remain limited in controllability for robotic manipulation. Recent works on trajectory-conditioned video generation address this gap but often rely on 2D trajectories or single modality conditioning, which restricts their ability to produce controllable and consistent robotic demonstrations. We present DRAW2ACT, a depth-aware trajectory-conditioned video generation framework that extracts multiple orthogonal representations from the input trajectory, capturing depth, semantics, shape and motion, and injects them into the diffusion model. Moreover, we propose to jointly generate spatially aligned RGB and depth videos, leveraging cross-modality attention mechanisms and depth supervision to enhance the spatio-temporal consistency. Finally, we introduce a multimodal policy model conditioned on the generated RGB and depth sequences to regress the robot's joint angles. Experiments on Bridge V2, Berkeley Autolab, and simulation benchmarks show that DRAW2ACT achieves superior visual fidelity and consistency while yielding higher manipulation success rates compared to existing baselines.

CHEM: Estimating and Understanding Hallucinations in Deep Learning for Image Processing

U-Net and other U-shaped architectures have achieved significant success in image deconvolution tasks. However, challenges have emerged, as these methods might generate unrealistic artifacts or hallucinations, which can interfere with analysis in safety-critical scenarios. This paper introduces a novel approach for quantifying and comprehending hallucination artifacts to ensure trustworthy computer vision models. Our method, termed the Conformal Hallucination Estimation Metric (CHEM), is applicable to any image reconstruction model, enabling efficient identification and quantification of hallucination artifacts. It offers two key advantages: it leverages wavelet and shearlet representations to efficiently extract hallucinations of image features and uses conformalized quantile regression to assess hallucination levels in a distribution-free manner. Furthermore, from an approximation theoretical perspective, we explore the reasons why U-shaped networks are prone to hallucinations. We test the proposed approach on the CANDELS astronomical image dataset with models such as U-Net, SwinUNet, and Learnlets, and provide new perspectives on hallucination from different aspects in deep learning-based image processing.

When is a System Discoverable from Data? Discovery Requires Chaos

The deep learning revolution has spurred a rise in advances of using AI in sciences. Within physical sciences the main focus has been on discovery of dynamical systems from observational data. Yet the reliability of learned surrogates and symbolic models is often undermined by the fundamental problem of non-uniqueness. The resulting models may fit the available data perfectly, but lack genuine predictive power. This raises the question: under what conditions can the systems governing equations be uniquely identified from a finite set of observations? We show, counter-intuitively, that chaos, typically associated with unpredictability, is crucial for ensuring a system is discoverable in the space of continuous or analytic functions. The prevalence of chaotic systems in benchmark datasets may have inadvertently obscured this fundamental limitation. More concretely, we show that systems chaotic on their entire domain are discoverable from a single trajectory within the space of continuous functions, and systems chaotic on a strange attractor are analytically discoverable under a geometric condition on the attractor. As a consequence, we demonstrate for the first time that the classical Lorenz system is analytically discoverable. Moreover, we establish that analytic discoverability is impossible in the presence of first integrals, common in real-world systems. These findings help explain the success of data-driven methods in inherently chaotic domains like weather forecasting, while revealing a significant challenge for engineering applications like digital twins, where stable, predictable behavior is desired. For these non-chaotic systems, we find that while trajectory data alone is insufficient, certain prior physical knowledge can help ensure discoverability. These findings warrant a critical re-evaluation of the fundamental assumptions underpinning purely data-driven discovery.

Improved probabilistic regression using diffusion models

Probabilistic regression models the entire predictive distribution of a response variable, offering richer insights than classical point estimates and directly allowing for uncertainty quantification. While diffusion-based generative models have shown remarkable success in generating complex, high-dimensional data, their usage in general regression tasks often lacks uncertainty-related evaluation and remains limited to domain-specific applications. We propose a novel diffusion-based framework for probabilistic regression that learns predictive distributions in a nonparametric way. More specifically, we propose to model the full distribution of the diffusion noise, enabling adaptation to diverse tasks and enhanced uncertainty quantification. We investigate different noise parameterizations, analyze their trade-offs, and evaluate our framework across a broad range of regression tasks, covering low- and high-dimensional settings. For several experiments, our approach shows superior performance against existing baselines, while delivering calibrated uncertainty estimates, demonstrating its versatility as a tool for probabilistic prediction.

RoboSwap: A GAN-driven Video Diffusion Framework For Unsupervised Robot Arm Swapping

Recent advancements in generative models have revolutionized video synthesis and editing. However, the scarcity of diverse, high-quality datasets continues to hinder video-conditioned robotic learning, limiting cross-platform generalization. In this work, we address the challenge of swapping a robotic arm in one video with another: a key step for crossembodiment learning. Unlike previous methods that depend on paired video demonstrations in the same environmental settings, our proposed framework, RoboSwap, operates on unpaired data from diverse environments, alleviating the data collection needs. RoboSwap introduces a novel video editing pipeline integrating both GANs and diffusion models, combining their isolated advantages. Specifically, we segment robotic arms from their backgrounds and train an unpaired GAN model to translate one robotic arm to another. The translated arm is blended with the original video background and refined with a diffusion model to enhance coherence, motion realism and object interaction. The GAN and diffusion stages are trained independently. Our experiments demonstrate that RoboSwap outperforms state-of-the-art video and image editing models on three benchmarks in terms of both structural coherence and motion consistency, thereby offering a robust solution for generating reliable, cross-embodiment data in robotic learning.

Conflicting Biases at the Edge of Stability: Norm versus Sharpness Regularization

A widely believed explanation for the remarkable generalization capacities of overparameterized neural networks is that the optimization algorithms used for training induce an implicit bias towards benign solutions. To grasp this theoretically, recent works examine gradient descent and its variants in simplified training settings, often assuming vanishing learning rates. These studies reveal various forms of implicit regularization, such as $\ell_1$-norm minimizing parameters in regression and max-margin solutions in classification. Concurrently, empirical findings show that moderate to large learning rates exceeding standard stability thresholds lead to faster, albeit oscillatory, convergence in the so-called Edge-of-Stability regime, and induce an implicit bias towards minima of low sharpness (norm of training loss Hessian). In this work, we argue that a comprehensive understanding of the generalization performance of gradient descent requires analyzing the interaction between these various forms of implicit regularization. We empirically demonstrate that the learning rate balances between low parameter norm and low sharpness of the trained model. We furthermore prove for diagonal linear networks trained on a simple regression task that neither implicit bias alone minimizes the generalization error. These findings demonstrate that focusing on a single implicit bias is insufficient to explain good generalization, and they motivate a broader view of implicit regularization that captures the dynamic trade-off between norm and sharpness induced by non-negligible learning rates.

Revisiting Glorot Initialization for Long-Range Linear Recurrences

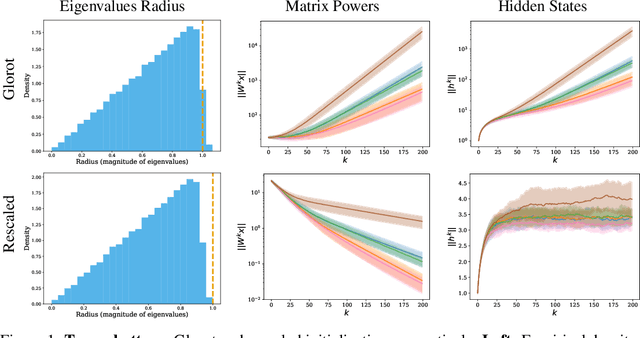
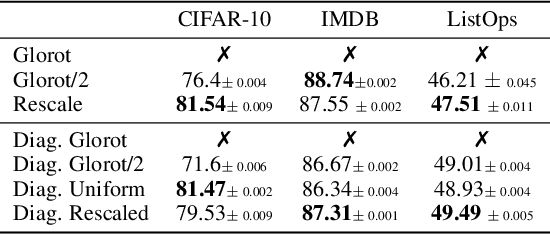
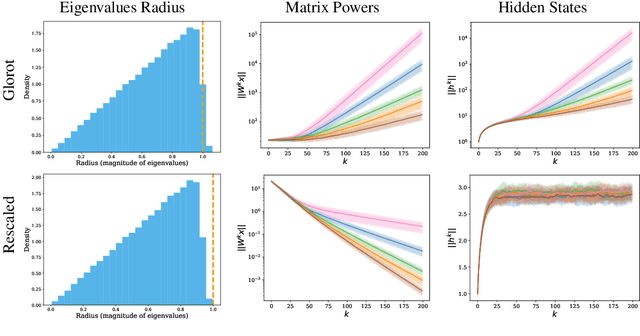
Proper initialization is critical for Recurrent Neural Networks (RNNs), particularly in long-range reasoning tasks, where repeated application of the same weight matrix can cause vanishing or exploding signals. A common baseline for linear recurrences is Glorot initialization, designed to ensure stable signal propagation--but derived under the infinite-width, fixed-length regime--an unrealistic setting for RNNs processing long sequences. In this work, we show that Glorot initialization is in fact unstable: small positive deviations in the spectral radius are amplified through time and cause the hidden state to explode. Our theoretical analysis demonstrates that sequences of length $t = O(\sqrt{n})$, where $n$ is the hidden width, are sufficient to induce instability. To address this, we propose a simple, dimension-aware rescaling of Glorot that shifts the spectral radius slightly below one, preventing rapid signal explosion or decay. These results suggest that standard initialization schemes may break down in the long-sequence regime, motivating a separate line of theory for stable recurrent initialization.

Time to Spike? Understanding the Representational Power of Spiking Neural Networks in Discrete Time

Recent years have seen significant progress in developing spiking neural networks (SNNs) as a potential solution to the energy challenges posed by conventional artificial neural networks (ANNs). However, our theoretical understanding of SNNs remains relatively limited compared to the ever-growing body of literature on ANNs. In this paper, we study a discrete-time model of SNNs based on leaky integrate-and-fire (LIF) neurons, referred to as discrete-time LIF-SNNs, a widely used framework that still lacks solid theoretical foundations. We demonstrate that discrete-time LIF-SNNs with static inputs and outputs realize piecewise constant functions defined on polyhedral regions, and more importantly, we quantify the network size required to approximate continuous functions. Moreover, we investigate the impact of latency (number of time steps) and depth (number of layers) on the complexity of the input space partitioning induced by discrete-time LIF-SNNs. Our analysis highlights the importance of latency and contrasts these networks with ANNs employing piecewise linear activation functions. Finally, we present numerical experiments to support our theoretical findings.

GradPCA: Leveraging NTK Alignment for Reliable Out-of-Distribution Detection

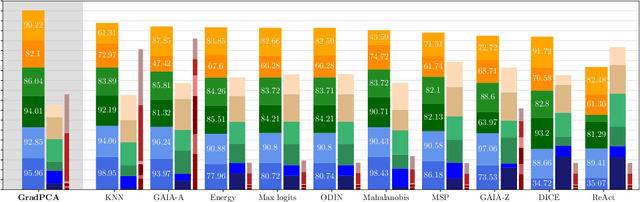
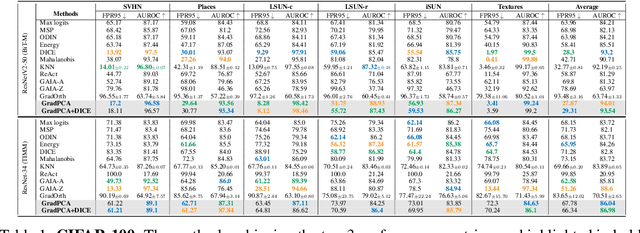
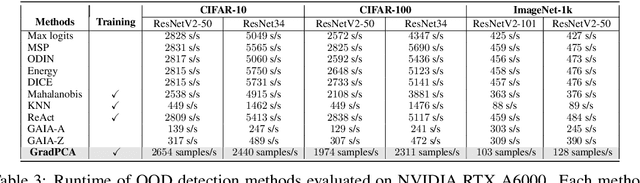
We introduce GradPCA, an Out-of-Distribution (OOD) detection method that exploits the low-rank structure of neural network gradients induced by Neural Tangent Kernel (NTK) alignment. GradPCA applies Principal Component Analysis (PCA) to gradient class-means, achieving more consistent performance than existing methods across standard image classification benchmarks. We provide a theoretical perspective on spectral OOD detection in neural networks to support GradPCA, highlighting feature-space properties that enable effective detection and naturally emerge from NTK alignment. Our analysis further reveals that feature quality -- particularly the use of pretrained versus non-pretrained representations -- plays a crucial role in determining which detectors will succeed. Extensive experiments validate the strong performance of GradPCA, and our theoretical framework offers guidance for designing more principled spectral OOD detectors.

Interpretable Robotic Friction Learning via Symbolic Regression

Accurately modeling the friction torque in robotic joints has long been challenging due to the request for a robust mathematical description. Traditional model-based approaches are often labor-intensive, requiring extensive experiments and expert knowledge, and they are difficult to adapt to new scenarios and dependencies. On the other hand, data-driven methods based on neural networks are easier to implement but often lack robustness, interpretability, and trustworthiness--key considerations for robotic hardware and safety-critical applications such as human-robot interaction. To address the limitations of both approaches, we propose the use of symbolic regression (SR) to estimate the friction torque. SR generates interpretable symbolic formulas similar to those produced by model-based methods while being flexible to accommodate various dynamic effects and dependencies. In this work, we apply SR algorithms to approximate the friction torque using collected data from a KUKA LWR-IV+ robot. Our results show that SR not only yields formulas with comparable complexity to model-based approaches but also achieves higher accuracy. Moreover, SR-derived formulas can be seamlessly extended to include load dependencies and other dynamic factors.