Graph Neural Networks for Enhancing Ensemble Forecasts of Extreme Rainfall

Climate change is increasing the occurrence of extreme precipitation events, threatening infrastructure, agriculture, and public safety. Ensemble prediction systems provide probabilistic forecasts but exhibit biases and difficulties in capturing extreme weather. While post-processing techniques aim to enhance forecast accuracy, they rarely focus on precipitation, which exhibits complex spatial dependencies and tail behavior. Our novel framework leverages graph neural networks to post-process ensemble forecasts, specifically modeling the extremes of the underlying distribution. This allows to capture spatial dependencies and improves forecast accuracy for extreme events, thus leading to more reliable forecasts and mitigating risks of extreme precipitation and flooding.

Probabilistic neural operators for functional uncertainty quantification

Neural operators aim to approximate the solution operator of a system of differential equations purely from data. They have shown immense success in modeling complex dynamical systems across various domains. However, the occurrence of uncertainties inherent in both model and data has so far rarely been taken into account\textemdash{}a critical limitation in complex, chaotic systems such as weather forecasting. In this paper, we introduce the probabilistic neural operator (PNO), a framework for learning probability distributions over the output function space of neural operators. PNO extends neural operators with generative modeling based on strictly proper scoring rules, integrating uncertainty information directly into the training process. We provide a theoretical justification for the approach and demonstrate improved performance in quantifying uncertainty across different domains and with respect to different baselines. Furthermore, PNO requires minimal adjustment to existing architectures, shows improved performance for most probabilistic prediction tasks, and leads to well-calibrated predictive distributions and adequate uncertainty representations even for long dynamical trajectories. Implementing our approach into large-scale models for physical applications can lead to improvements in corresponding uncertainty quantification and extreme event identification, ultimately leading to a deeper understanding of the prediction of such surrogate models.

Robust identifiability for symbolic recovery of differential equations

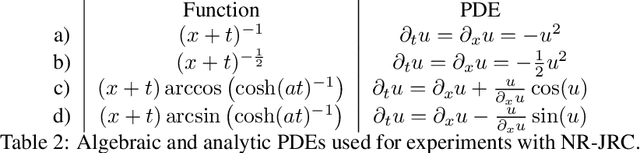
Recent advancements in machine learning have transformed the discovery of physical laws, moving from manual derivation to data-driven methods that simultaneously learn both the structure and parameters of governing equations. This shift introduces new challenges regarding the validity of the discovered equations, particularly concerning their uniqueness and, hence, identifiability. While the issue of non-uniqueness has been well-studied in the context of parameter estimation, it remains underexplored for algorithms that recover both structure and parameters simultaneously. Early studies have primarily focused on idealized scenarios with perfect, noise-free data. In contrast, this paper investigates how noise influences the uniqueness and identifiability of physical laws governed by partial differential equations (PDEs). We develop a comprehensive mathematical framework to analyze the uniqueness of PDEs in the presence of noise and introduce new algorithms that account for noise, providing thresholds to assess uniqueness and identifying situations where excessive noise hinders reliable conclusions. Numerical experiments demonstrate the effectiveness of these algorithms in detecting uniqueness despite the presence of noise.

Learning-based adaption of robotic friction models

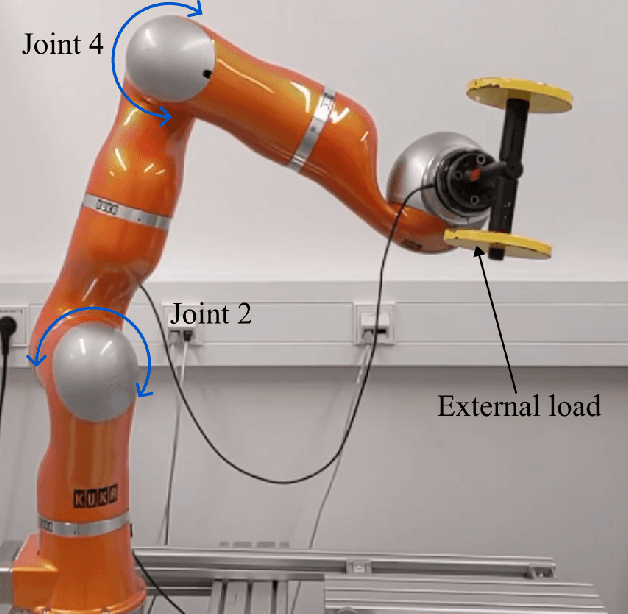
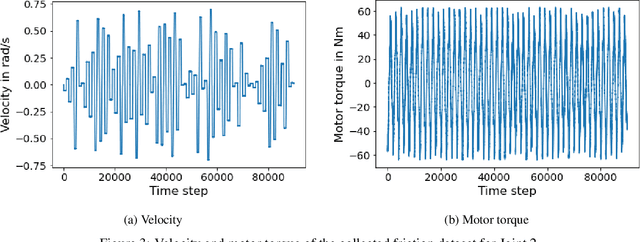
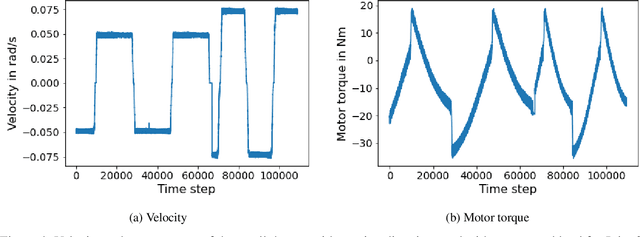
In the Fourth Industrial Revolution, wherein artificial intelligence and the automation of machines occupy a central role, the deployment of robots is indispensable. However, the manufacturing process using robots, especially in collaboration with humans, is highly intricate. In particular, modeling the friction torque in robotic joints is a longstanding problem due to the lack of a good mathematical description. This motivates the usage of data-driven methods in recent works. However, model-based and data-driven models often exhibit limitations in their ability to generalize beyond the specific dynamics they were trained on, as we demonstrate in this paper. To address this challenge, we introduce a novel approach based on residual learning, which aims to adapt an existing friction model to new dynamics using as little data as possible. We validate our approach by training a base neural network on a symmetric friction data set to learn an accurate relation between the velocity and the friction torque. Subsequently, to adapt to more complex asymmetric settings, we train a second network on a small dataset, focusing on predicting the residual of the initial network's output. By combining the output of both networks in a suitable manner, our proposed estimator outperforms the conventional model-based approach and the base neural network significantly. Furthermore, we evaluate our method on trajectories involving external loads and still observe a substantial improvement, approximately 60-70\%, over the conventional approach. Our method does not rely on data with external load during training, eliminating the need for external torque sensors. This demonstrates the generalization capability of our approach, even with a small amount of data-only 43 seconds of a robot movement-enabling adaptation to diverse scenarios based on prior knowledge about friction in different settings.

ParFam -- Symbolic Regression Based on Continuous Global Optimization

The problem of symbolic regression (SR) arises in many different applications, such as identifying physical laws or deriving mathematical equations describing the behavior of financial markets from given data. Various methods exist to address the problem of SR, often based on genetic programming. However, these methods are usually quite complicated and require a lot of hyperparameter tuning and computational resources. In this paper, we present our new method ParFam that utilizes parametric families of suitable symbolic functions to translate the discrete symbolic regression problem into a continuous one, resulting in a more straightforward setup compared to current state-of-the-art methods. In combination with a powerful global optimizer, this approach results in an effective method to tackle the problem of SR. Furthermore, it can be easily extended to more advanced algorithms, e.g., by adding a deep neural network to find good-fitting parametric families. We prove the performance of ParFam with extensive numerical experiments based on the common SR benchmark suit SRBench, showing that we achieve state-of-the-art results. Our code and results can be found at https://github.com/Philipp238/parfam .

Well-definedness of Physical Law Learning: The Uniqueness Problem

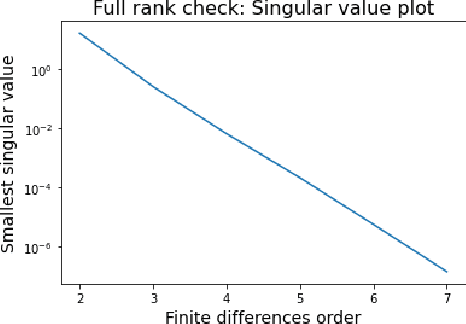
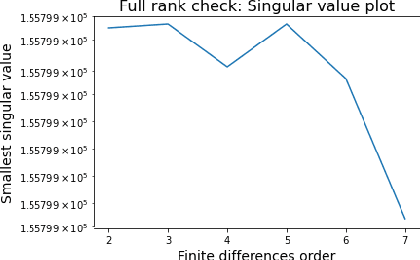
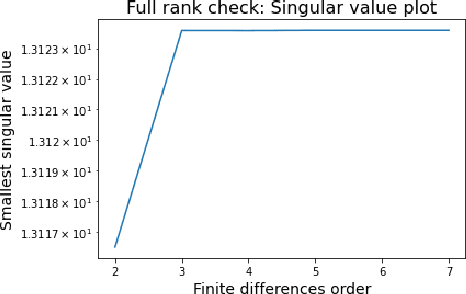
Physical law learning is the ambiguous attempt at automating the derivation of governing equations with the use of machine learning techniques. The current literature focuses however solely on the development of methods to achieve this goal, and a theoretical foundation is at present missing. This paper shall thus serve as a first step to build a comprehensive theoretical framework for learning physical laws, aiming to provide reliability to according algorithms. One key problem consists in the fact that the governing equations might not be uniquely determined by the given data. We will study this problem in the common situation of having a physical law be described by an ordinary or partial differential equation. For various different classes of differential equations, we provide both necessary and sufficient conditions for a function from a given function class to uniquely determine the differential equation which is governing the phenomenon. We then use our results to devise numerical algorithms to determine whether a function solves a differential equation uniquely. Finally, we provide extensive numerical experiments showing that our algorithms in combination with common approaches for learning physical laws indeed allow to guarantee that a unique governing differential equation is learnt, without assuming any knowledge about the function, thereby ensuring reliability.

Safe Policy Improvement Approaches and their Limitations

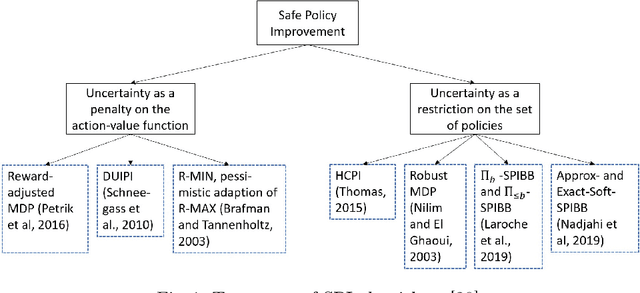
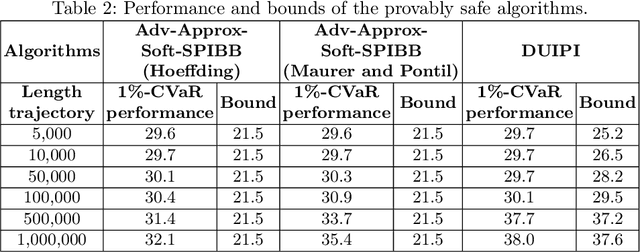
Safe Policy Improvement (SPI) is an important technique for offline reinforcement learning in safety critical applications as it improves the behavior policy with a high probability. We classify various SPI approaches from the literature into two groups, based on how they utilize the uncertainty of state-action pairs. Focusing on the Soft-SPIBB (Safe Policy Improvement with Soft Baseline Bootstrapping) algorithms, we show that their claim of being provably safe does not hold. Based on this finding, we develop adaptations, the Adv-Soft-SPIBB algorithms, and show that they are provably safe. A heuristic adaptation, Lower-Approx-Soft-SPIBB, yields the best performance among all SPIBB algorithms in extensive experiments on two benchmarks. We also check the safety guarantees of the provably safe algorithms and show that huge amounts of data are necessary such that the safety bounds become useful in practice.

Safe Policy Improvement Approaches on Discrete Markov Decision Processes

Safe Policy Improvement (SPI) aims at provable guarantees that a learned policy is at least approximately as good as a given baseline policy. Building on SPI with Soft Baseline Bootstrapping (Soft-SPIBB) by Nadjahi et al., we identify theoretical issues in their approach, provide a corrected theory, and derive a new algorithm that is provably safe on finite Markov Decision Processes (MDP). Additionally, we provide a heuristic algorithm that exhibits the best performance among many state of the art SPI algorithms on two different benchmarks. Furthermore, we introduce a taxonomy of SPI algorithms and empirically show an interesting property of two classes of SPI algorithms: while the mean performance of algorithms that incorporate the uncertainty as a penalty on the action-value is higher, actively restricting the set of policies more consistently produces good policies and is, thus, safer.