Robust identifiability for symbolic recovery of differential equations

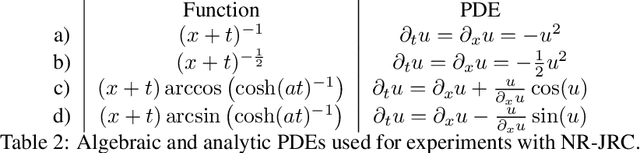
Recent advancements in machine learning have transformed the discovery of physical laws, moving from manual derivation to data-driven methods that simultaneously learn both the structure and parameters of governing equations. This shift introduces new challenges regarding the validity of the discovered equations, particularly concerning their uniqueness and, hence, identifiability. While the issue of non-uniqueness has been well-studied in the context of parameter estimation, it remains underexplored for algorithms that recover both structure and parameters simultaneously. Early studies have primarily focused on idealized scenarios with perfect, noise-free data. In contrast, this paper investigates how noise influences the uniqueness and identifiability of physical laws governed by partial differential equations (PDEs). We develop a comprehensive mathematical framework to analyze the uniqueness of PDEs in the presence of noise and introduce new algorithms that account for noise, providing thresholds to assess uniqueness and identifying situations where excessive noise hinders reliable conclusions. Numerical experiments demonstrate the effectiveness of these algorithms in detecting uniqueness despite the presence of noise.

ParFam -- Symbolic Regression Based on Continuous Global Optimization

The problem of symbolic regression (SR) arises in many different applications, such as identifying physical laws or deriving mathematical equations describing the behavior of financial markets from given data. Various methods exist to address the problem of SR, often based on genetic programming. However, these methods are usually quite complicated and require a lot of hyperparameter tuning and computational resources. In this paper, we present our new method ParFam that utilizes parametric families of suitable symbolic functions to translate the discrete symbolic regression problem into a continuous one, resulting in a more straightforward setup compared to current state-of-the-art methods. In combination with a powerful global optimizer, this approach results in an effective method to tackle the problem of SR. Furthermore, it can be easily extended to more advanced algorithms, e.g., by adding a deep neural network to find good-fitting parametric families. We prove the performance of ParFam with extensive numerical experiments based on the common SR benchmark suit SRBench, showing that we achieve state-of-the-art results. Our code and results can be found at https://github.com/Philipp238/parfam .