ParFam -- Symbolic Regression Based on Continuous Global Optimization

The problem of symbolic regression (SR) arises in many different applications, such as identifying physical laws or deriving mathematical equations describing the behavior of financial markets from given data. Various methods exist to address the problem of SR, often based on genetic programming. However, these methods are usually quite complicated and require a lot of hyperparameter tuning and computational resources. In this paper, we present our new method ParFam that utilizes parametric families of suitable symbolic functions to translate the discrete symbolic regression problem into a continuous one, resulting in a more straightforward setup compared to current state-of-the-art methods. In combination with a powerful global optimizer, this approach results in an effective method to tackle the problem of SR. Furthermore, it can be easily extended to more advanced algorithms, e.g., by adding a deep neural network to find good-fitting parametric families. We prove the performance of ParFam with extensive numerical experiments based on the common SR benchmark suit SRBench, showing that we achieve state-of-the-art results. Our code and results can be found at https://github.com/Philipp238/parfam .

On the Universal Transformation of Data-Driven Models to Control Systems

As in almost every other branch of science, the major advances in data science and machine learning have also resulted in significant improvements regarding the modeling and simulation of nonlinear dynamical systems. It is nowadays possible to make accurate medium to long-term predictions of highly complex systems such as the weather, the dynamics within a nuclear fusion reactor, of disease models or the stock market in a very efficient manner. In many cases, predictive methods are advertised to ultimately be useful for control, as the control of high-dimensional nonlinear systems is an engineering grand challenge with huge potential in areas such as clean and efficient energy production, or the development of advanced medical devices. However, the question of how to use a predictive model for control is often left unanswered due to the associated challenges, namely a significantly higher system complexity, the requirement of much larger data sets and an increased and often problem-specific modeling effort. To solve these issues, we present a universal framework (which we call QuaSiModO: Quantization-Simulation-Modeling-Optimization) to transform arbitrary predictive models into control systems and use them for feedback control. The advantages of our approach are a linear increase in data requirements with respect to the control dimension, performance guarantees that rely exclusively on the accuracy of the predictive model, and only little prior knowledge requirements in control theory to solve complex control problems. In particular the latter point is of key importance to enable a large number of researchers and practitioners to exploit the ever increasing capabilities of predictive models for control in a straight-forward and systematic fashion.

On the Treatment of Optimization Problems with L1 Penalty Terms via Multiobjective Continuation

We present a novel algorithm that allows us to gain detailed insight into the effects of sparsity in linear and nonlinear optimization, which is of great importance in many scientific areas such as image and signal processing, medical imaging, compressed sensing, and machine learning (e.g., for the training of neural networks). Sparsity is an important feature to ensure robustness against noisy data, but also to find models that are interpretable and easy to analyze due to the small number of relevant terms. It is common practice to enforce sparsity by adding the $\ell_1$-norm as a weighted penalty term. In order to gain a better understanding and to allow for an informed model selection, we directly solve the corresponding multiobjective optimization problem (MOP) that arises when we minimize the main objective and the $\ell_1$-norm simultaneously. As this MOP is in general non-convex for nonlinear objectives, the weighting method will fail to provide all optimal compromises. To avoid this issue, we present a continuation method which is specifically tailored to MOPs with two objective functions one of which is the $\ell_1$-norm. Our method can be seen as a generalization of well-known homotopy methods for linear regression problems to the nonlinear case. Several numerical examples - including neural network training - demonstrate our theoretical findings and the additional insight that can be gained by this multiobjective approach.

Deep Model Predictive Control with Online Learning for Complex Physical Systems

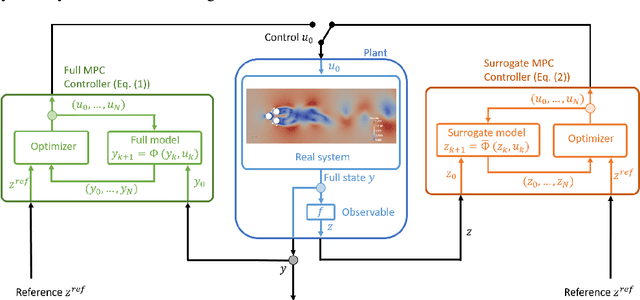
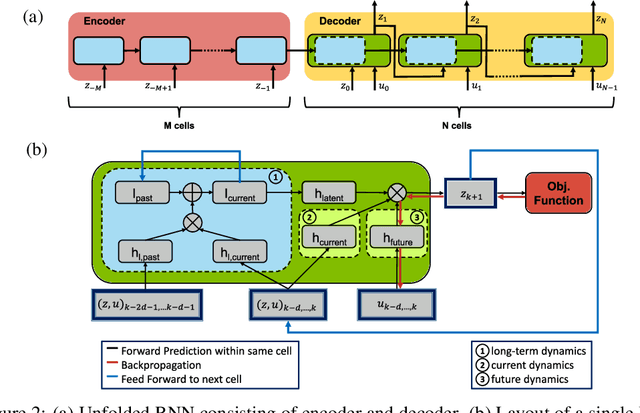
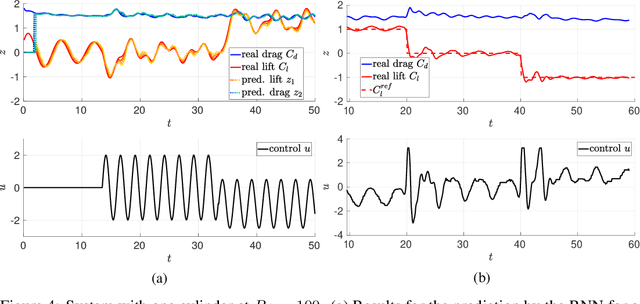
The control of complex systems is of critical importance in many branches of science, engineering, and industry. Controlling an unsteady fluid flow is particularly important, as flow control is a key enabler for technologies in energy (e.g., wind, tidal, and combustion), transportation (e.g., planes, trains, and automobiles), security (e.g., tracking airborne contamination), and health (e.g., artificial hearts and artificial respiration). However, the high-dimensional, nonlinear, and multi-scale dynamics make real-time feedback control infeasible. Fortunately, these high-dimensional systems exhibit dominant, low-dimensional patterns of activity that can be exploited for effective control in the sense that knowledge of the entire state of a system is not required. Advances in machine learning have the potential to revolutionize flow control given its ability to extract principled, low-rank feature spaces characterizing such complex systems. We present a novel deep learning model predictive control (DeepMPC) framework that exploits low-rank features of the flow in order to achieve considerable improvements to control performance. Instead of predicting the entire fluid state, we use a recurrent neural network (RNN) to accurately predict the control relevant quantities of the system. The RNN is then embedded into a MPC framework to construct a feedback loop, and incoming sensor data is used to perform online updates to improve prediction accuracy. The results are validated using varying fluid flow examples of increasing complexity.