Efficient time stepping for numerical integration using reinforcement learning

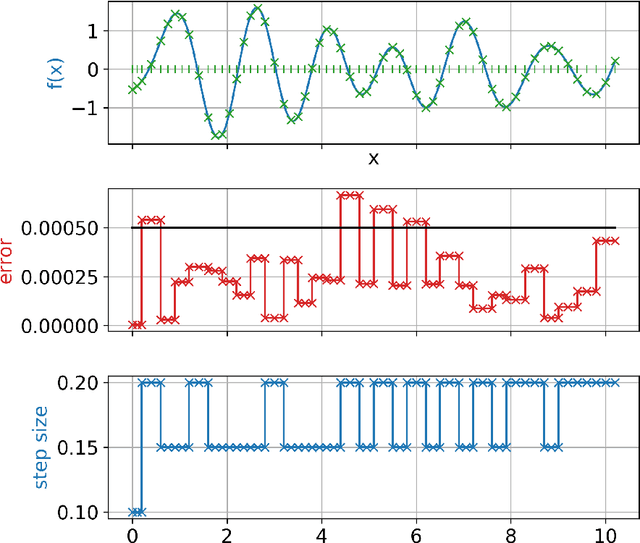
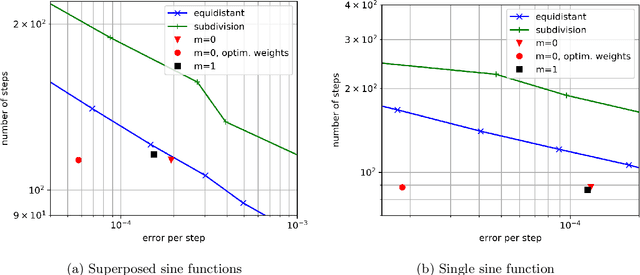
Many problems in science and engineering require the efficient numerical approximation of integrals, a particularly important application being the numerical solution of initial value problems for differential equations. For complex systems, an equidistant discretization is often inadvisable, as it either results in prohibitively large errors or computational effort. To this end, adaptive schemes have been developed that rely on error estimators based on Taylor series expansions. While these estimators a) rely on strong smoothness assumptions and b) may still result in erroneous steps for complex systems (and thus require step rejection mechanisms), we here propose a data-driven time stepping scheme based on machine learning, and more specifically on reinforcement learning (RL) and meta-learning. First, one or several (in the case of non-smooth or hybrid systems) base learners are trained using RL. Then, a meta-learner is trained which (depending on the system state) selects the base learner that appears to be optimal for the current situation. Several examples including both smooth and non-smooth problems demonstrate the superior performance of our approach over state-of-the-art numerical schemes. The code is available under https://github.com/lueckem/quadrature-ML.

Deep Model Predictive Control with Online Learning for Complex Physical Systems

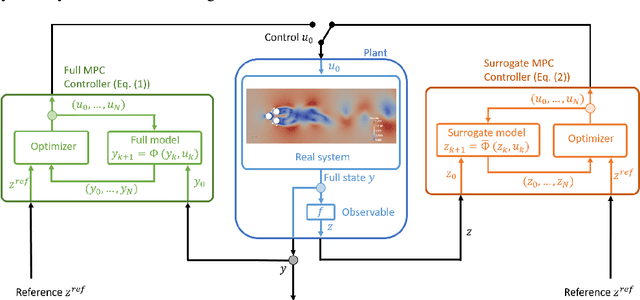
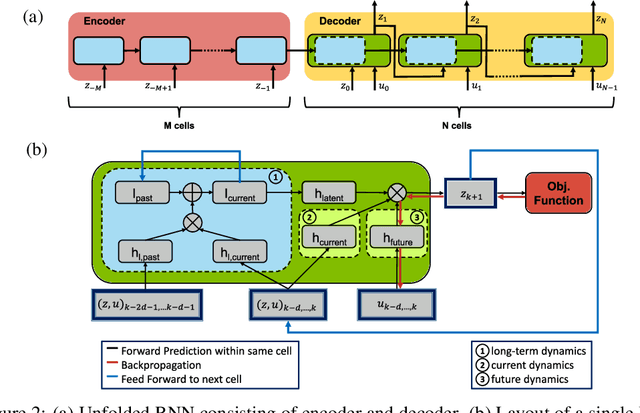
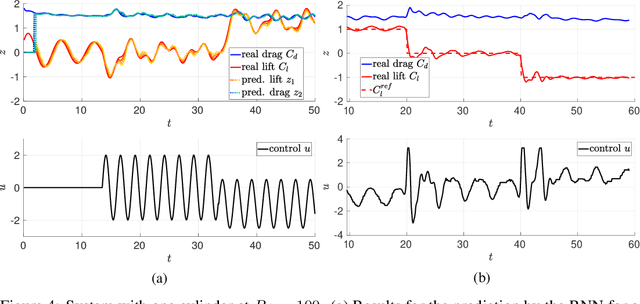
The control of complex systems is of critical importance in many branches of science, engineering, and industry. Controlling an unsteady fluid flow is particularly important, as flow control is a key enabler for technologies in energy (e.g., wind, tidal, and combustion), transportation (e.g., planes, trains, and automobiles), security (e.g., tracking airborne contamination), and health (e.g., artificial hearts and artificial respiration). However, the high-dimensional, nonlinear, and multi-scale dynamics make real-time feedback control infeasible. Fortunately, these high-dimensional systems exhibit dominant, low-dimensional patterns of activity that can be exploited for effective control in the sense that knowledge of the entire state of a system is not required. Advances in machine learning have the potential to revolutionize flow control given its ability to extract principled, low-rank feature spaces characterizing such complex systems. We present a novel deep learning model predictive control (DeepMPC) framework that exploits low-rank features of the flow in order to achieve considerable improvements to control performance. Instead of predicting the entire fluid state, we use a recurrent neural network (RNN) to accurately predict the control relevant quantities of the system. The RNN is then embedded into a MPC framework to construct a feedback loop, and incoming sensor data is used to perform online updates to improve prediction accuracy. The results are validated using varying fluid flow examples of increasing complexity.

A Traveling Salesman Learns Bayesian Networks

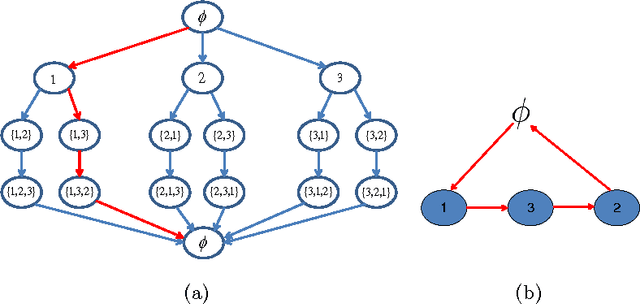
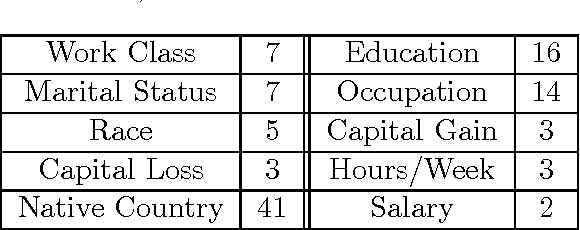
Structure learning of Bayesian networks is an important problem that arises in numerous machine learning applications. In this work, we present a novel approach for learning the structure of Bayesian networks using the solution of an appropriately constructed traveling salesman problem. In our approach, one computes an optimal ordering (partially ordered set) of random variables using methods for the traveling salesman problem. This ordering significantly reduces the search space for the subsequent greedy optimization that computes the final structure of the Bayesian network. We demonstrate our approach of learning Bayesian networks on real world census and weather datasets. In both cases, we demonstrate that the approach very accurately captures dependencies between random variables. We check the accuracy of the predictions based on independent studies in both application domains.