Efficient time stepping for numerical integration using reinforcement learning

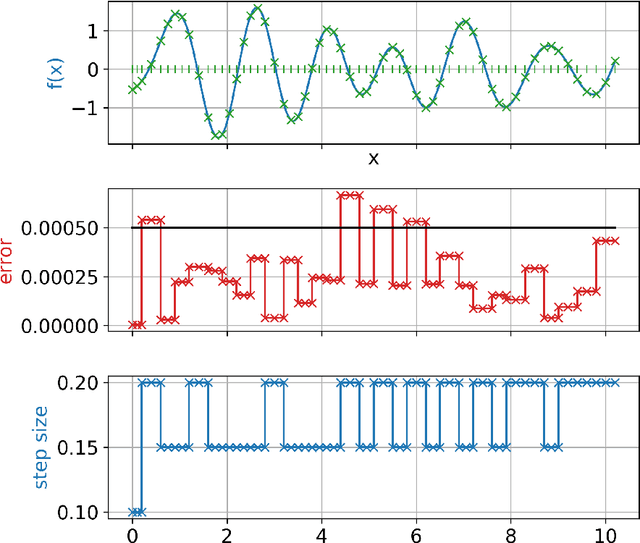
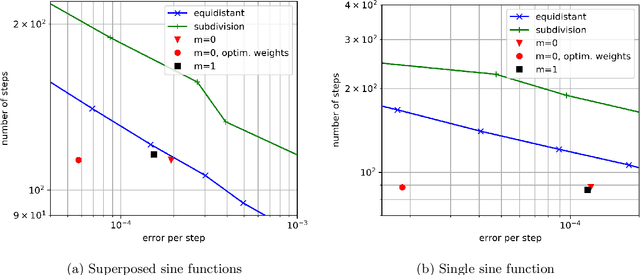
Many problems in science and engineering require the efficient numerical approximation of integrals, a particularly important application being the numerical solution of initial value problems for differential equations. For complex systems, an equidistant discretization is often inadvisable, as it either results in prohibitively large errors or computational effort. To this end, adaptive schemes have been developed that rely on error estimators based on Taylor series expansions. While these estimators a) rely on strong smoothness assumptions and b) may still result in erroneous steps for complex systems (and thus require step rejection mechanisms), we here propose a data-driven time stepping scheme based on machine learning, and more specifically on reinforcement learning (RL) and meta-learning. First, one or several (in the case of non-smooth or hybrid systems) base learners are trained using RL. Then, a meta-learner is trained which (depending on the system state) selects the base learner that appears to be optimal for the current situation. Several examples including both smooth and non-smooth problems demonstrate the superior performance of our approach over state-of-the-art numerical schemes. The code is available under https://github.com/lueckem/quadrature-ML.

Learning Choice Functions via Pareto-Embeddings

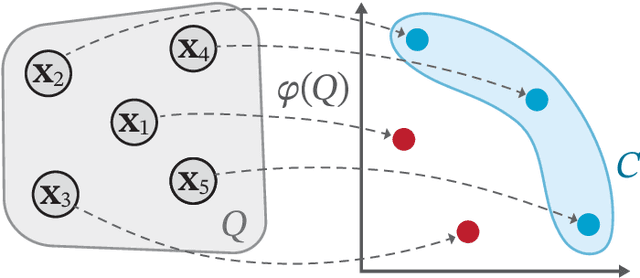
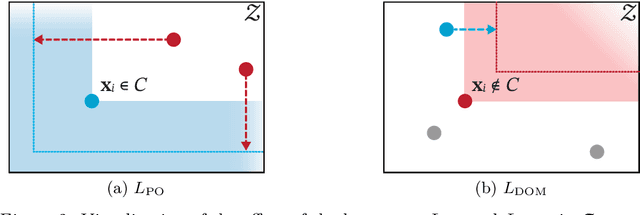
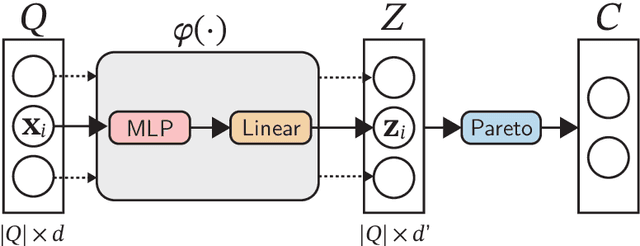
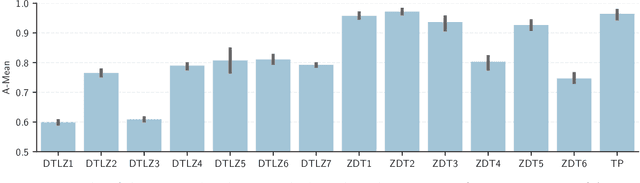
We consider the problem of learning to choose from a given set of objects, where each object is represented by a feature vector. Traditional approaches in choice modelling are mainly based on learning a latent, real-valued utility function, thereby inducing a linear order on choice alternatives. While this approach is suitable for discrete (top-1) choices, it is not straightforward how to use it for subset choices. Instead of mapping choice alternatives to the real number line, we propose to embed them into a higher-dimensional utility space, in which we identify choice sets with Pareto-optimal points. To this end, we propose a learning algorithm that minimizes a differentiable loss function suitable for this task. We demonstrate the feasibility of learning a Pareto-embedding on a suite of benchmark datasets.

Learning Choice Functions

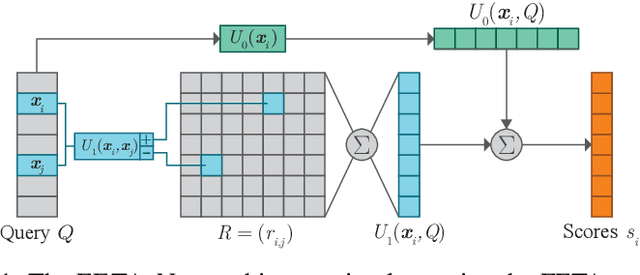
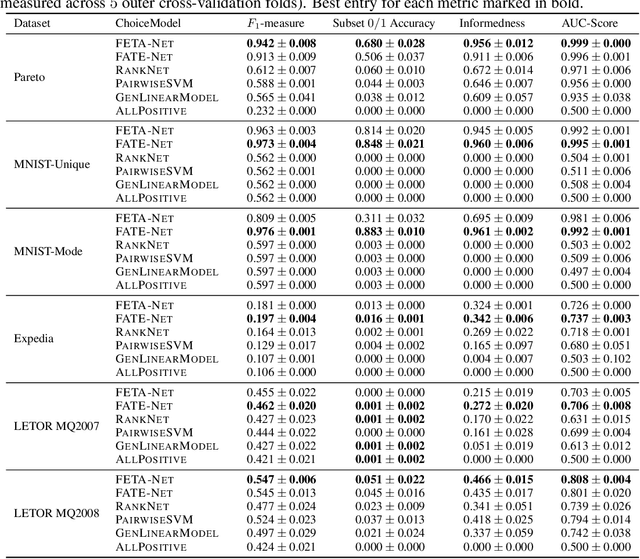
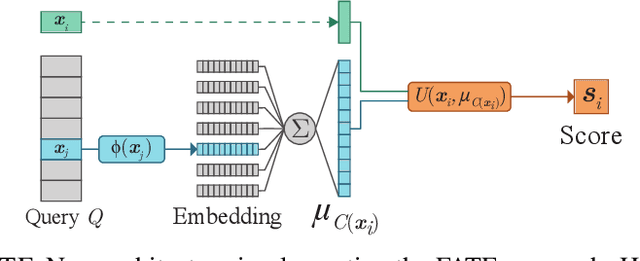
We study the problem of learning choice functions, which play an important role in various domains of application, most notably in the field of economics. Formally, a choice function is a mapping from sets to sets: Given a set of choice alternatives as input, a choice function identifies a subset of most preferred elements. Learning choice functions from suitable training data comes with a number of challenges. For example, the sets provided as input and the subsets produced as output can be of any size. Moreover, since the order in which alternatives are presented is irrelevant, a choice function should be symmetric. Perhaps most importantly, choice functions are naturally context-dependent, in the sense that the preference in favor of an alternative may depend on what other options are available. We formalize the problem of learning choice functions and present two general approaches based on two representations of context-dependent utility functions. Both approaches are instantiated by means of appropriate neural network architectures, and their performance is demonstrated on suitable benchmark tasks.

Deep architectures for learning context-dependent ranking functions

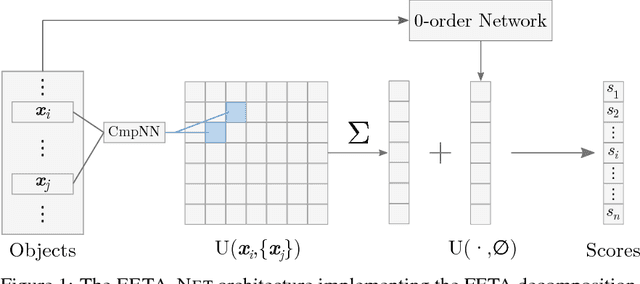
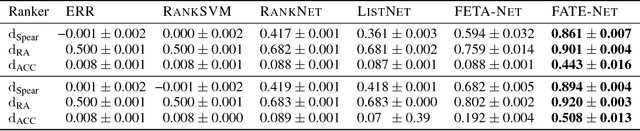
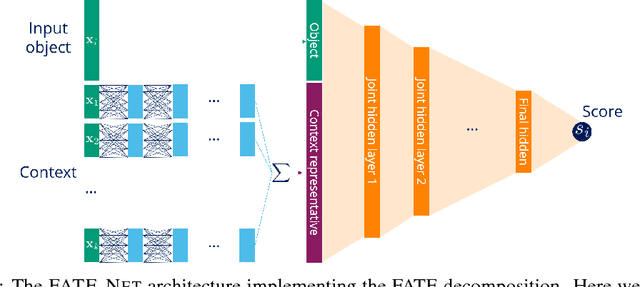
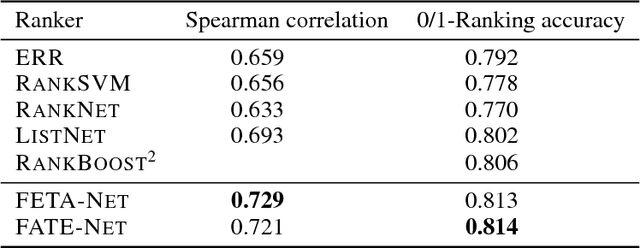
Object ranking is an important problem in the realm of preference learning. On the basis of training data in the form of a set of rankings of objects, which are typically represented as feature vectors, the goal is to learn a ranking function that predicts a linear order of any new set of objects. Current approaches commonly focus on ranking by scoring, i.e., on learning an underlying latent utility function that seeks to capture the inherent utility of each object. These approaches, however, are not able to take possible effects of context-dependence into account, where context-dependence means that the utility or usefulness of an object may also depend on what other objects are available as alternatives. In this paper, we formalize the problem of context-dependent ranking and present two general approaches based on two natural representations of context-dependent ranking functions. Both approaches are instantiated by means of appropriate neural network architectures. We demonstrate empirically that our methods outperform traditional approaches on benchmark tasks, for which context-dependence is playing a relevant role.