Information Leakage Detection through Approximate Bayes-optimal Prediction

In today's data-driven world, the proliferation of publicly available information intensifies the challenge of information leakage (IL), raising security concerns. IL involves unintentionally exposing secret (sensitive) information to unauthorized parties via systems' observable information. Conventional statistical approaches, which estimate mutual information (MI) between observable and secret information for detecting IL, face challenges such as the curse of dimensionality, convergence, computational complexity, and MI misestimation. Furthermore, emerging supervised machine learning (ML) methods, though effective, are limited to binary system-sensitive information and lack a comprehensive theoretical framework. To address these limitations, we establish a theoretical framework using statistical learning theory and information theory to accurately quantify and detect IL. We demonstrate that MI can be accurately estimated by approximating the log-loss and accuracy of the Bayes predictor. As the Bayes predictor is typically unknown in practice, we propose to approximate it with the help of automated machine learning (AutoML). First, we compare our MI estimation approaches against current baselines, using synthetic data sets generated using the multivariate normal (MVN) distribution with known MI. Second, we introduce a cut-off technique using one-sided statistical tests to detect IL, employing the Holm-Bonferroni correction to increase confidence in detection decisions. Our study evaluates IL detection performance on real-world data sets, highlighting the effectiveness of the Bayes predictor's log-loss estimation, and finds our proposed method to effectively estimate MI on synthetic data sets and thus detect ILs accurately.

Meta-Learning for Automated Selection of Anomaly Detectors for Semi-Supervised Datasets

In anomaly detection, a prominent task is to induce a model to identify anomalies learned solely based on normal data. Generally, one is interested in finding an anomaly detector that correctly identifies anomalies, i.e., data points that do not belong to the normal class, without raising too many false alarms. Which anomaly detector is best suited depends on the dataset at hand and thus needs to be tailored. The quality of an anomaly detector may be assessed via confusion-based metrics such as the Matthews correlation coefficient (MCC). However, since during training only normal data is available in a semi-supervised setting, such metrics are not accessible. To facilitate automated machine learning for anomaly detectors, we propose to employ meta-learning to predict MCC scores based on metrics that can be computed with normal data only. First promising results can be obtained considering the hypervolume and the false positive rate as meta-features.

Learning Choice Functions

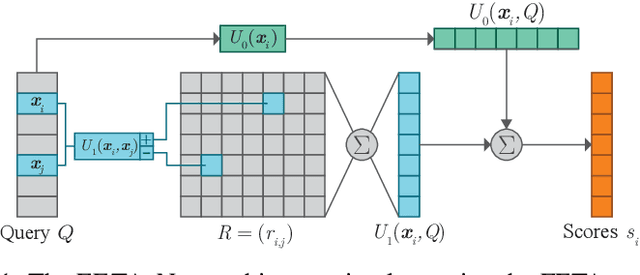
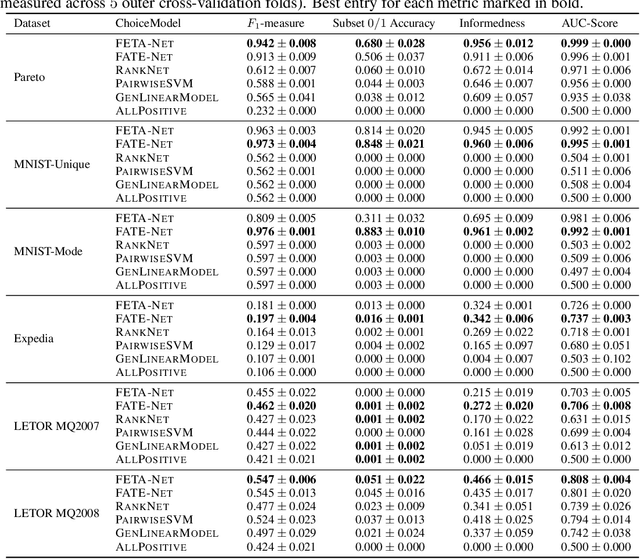
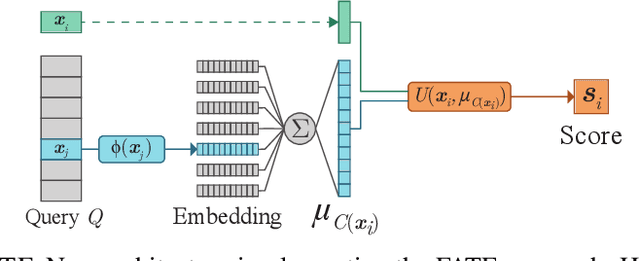
We study the problem of learning choice functions, which play an important role in various domains of application, most notably in the field of economics. Formally, a choice function is a mapping from sets to sets: Given a set of choice alternatives as input, a choice function identifies a subset of most preferred elements. Learning choice functions from suitable training data comes with a number of challenges. For example, the sets provided as input and the subsets produced as output can be of any size. Moreover, since the order in which alternatives are presented is irrelevant, a choice function should be symmetric. Perhaps most importantly, choice functions are naturally context-dependent, in the sense that the preference in favor of an alternative may depend on what other options are available. We formalize the problem of learning choice functions and present two general approaches based on two representations of context-dependent utility functions. Both approaches are instantiated by means of appropriate neural network architectures, and their performance is demonstrated on suitable benchmark tasks.

Deep architectures for learning context-dependent ranking functions

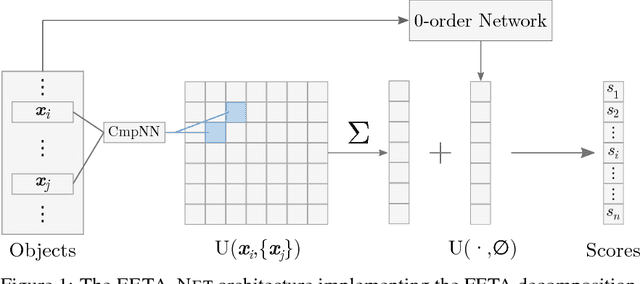
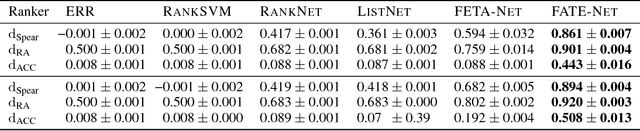
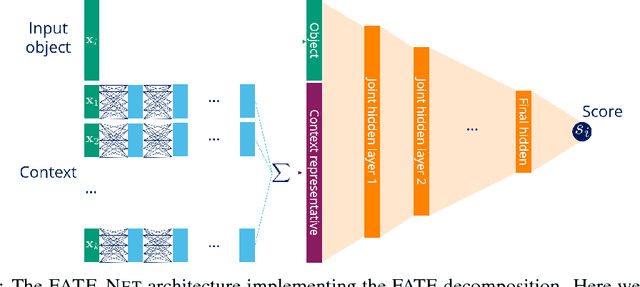
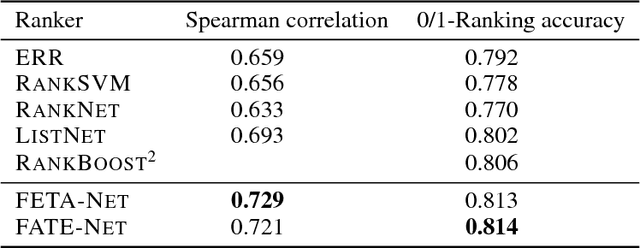
Object ranking is an important problem in the realm of preference learning. On the basis of training data in the form of a set of rankings of objects, which are typically represented as feature vectors, the goal is to learn a ranking function that predicts a linear order of any new set of objects. Current approaches commonly focus on ranking by scoring, i.e., on learning an underlying latent utility function that seeks to capture the inherent utility of each object. These approaches, however, are not able to take possible effects of context-dependence into account, where context-dependence means that the utility or usefulness of an object may also depend on what other objects are available as alternatives. In this paper, we formalize the problem of context-dependent ranking and present two general approaches based on two natural representations of context-dependent ranking functions. Both approaches are instantiated by means of appropriate neural network architectures. We demonstrate empirically that our methods outperform traditional approaches on benchmark tasks, for which context-dependence is playing a relevant role.