math-PVS: A Large Language Model Framework to Map Scientific Publications to PVS Theories

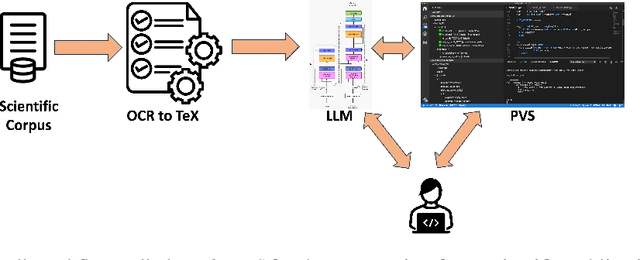
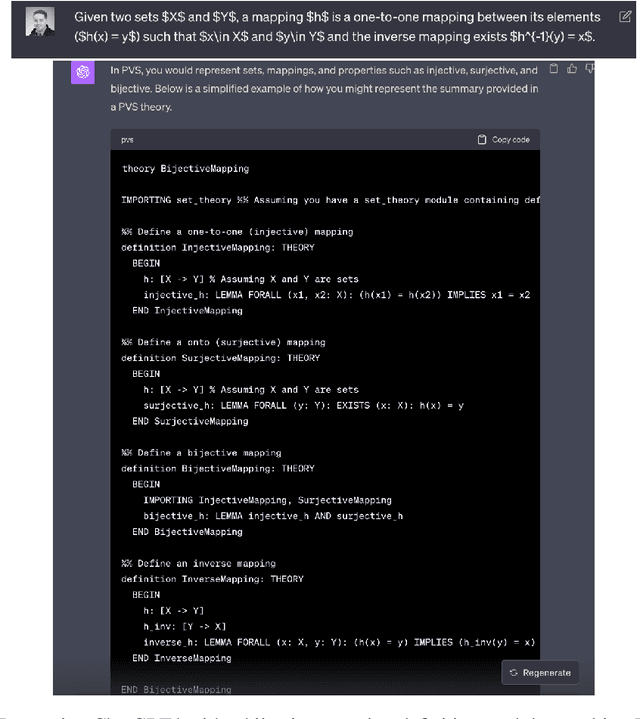
As artificial intelligence (AI) gains greater adoption in a wide variety of applications, it has immense potential to contribute to mathematical discovery, by guiding conjecture generation, constructing counterexamples, assisting in formalizing mathematics, and discovering connections between different mathematical areas, to name a few. While prior work has leveraged computers for exhaustive mathematical proof search, recent efforts based on large language models (LLMs) aspire to position computing platforms as co-contributors in the mathematical research process. Despite their current limitations in logic and mathematical tasks, there is growing interest in melding theorem proving systems with foundation models. This work investigates the applicability of LLMs in formalizing advanced mathematical concepts and proposes a framework that can critically review and check mathematical reasoning in research papers. Given the noted reasoning shortcomings of LLMs, our approach synergizes the capabilities of proof assistants, specifically PVS, with LLMs, enabling a bridge between textual descriptions in academic papers and formal specifications in PVS. By harnessing the PVS environment, coupled with data ingestion and conversion mechanisms, we envision an automated process, called \emph{math-PVS}, to extract and formalize mathematical theorems from research papers, offering an innovative tool for academic review and discovery.

A Dynamic Mode Decomposition Approach for Decentralized Spectral Clustering of Graphs

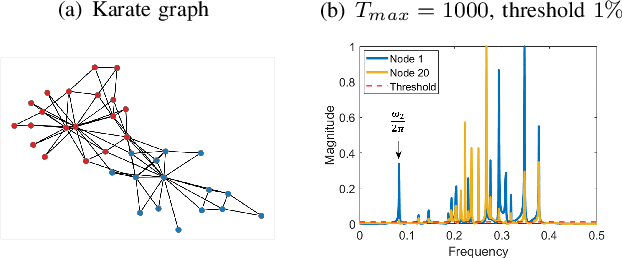
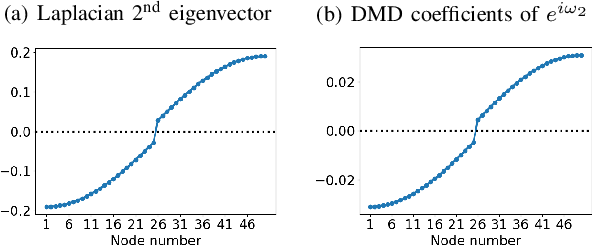
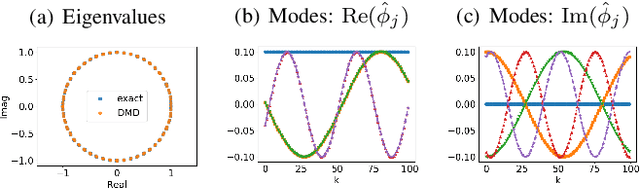
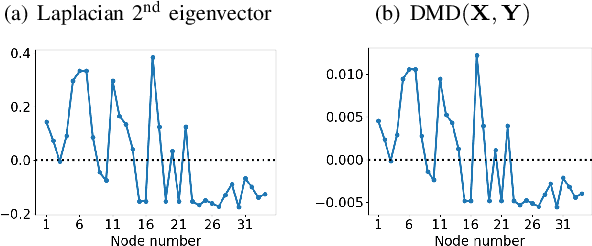
We propose a novel robust decentralized graph clustering algorithm that is provably equivalent to the popular spectral clustering approach. Our proposed method uses the existing wave equation clustering algorithm that is based on propagating waves through the graph. However, instead of using a fast Fourier transform (FFT) computation at every node, our proposed approach exploits the Koopman operator framework. Specifically, we show that propagating waves in the graph followed by a local dynamic mode decomposition (DMD) computation at every node is capable of retrieving the eigenvalues and the local eigenvector components of the graph Laplacian, thereby providing local cluster assignments for all nodes. We demonstrate that the DMD computation is more robust than the existing FFT based approach and requires 20 times fewer steps of the wave equation to accurately recover the clustering information and reduces the relative error by orders of magnitude. We demonstrate the decentralized approach on a range of graph clustering problems.

Post Quantum Secure Command and Control of Mobile Agents : Inserting quantum-resistant encryption schemes in the Secure Robot Operating System

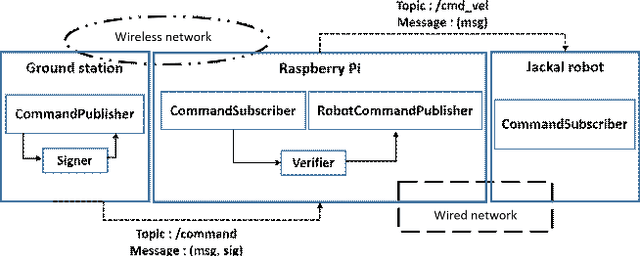
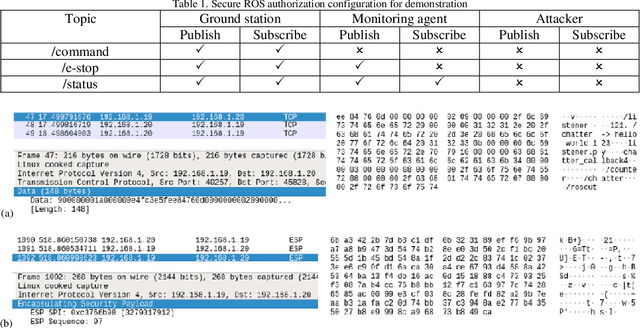
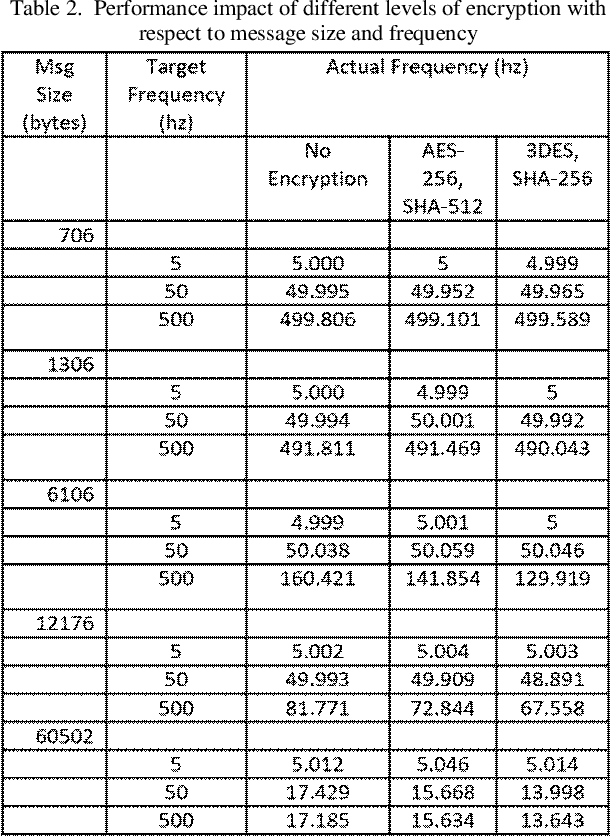
The secure command and control (C&C) of mobile agents arises in various settings including unmanned aerial vehicles, single pilot operations in commercial settings, and mobile robots to name a few. As more and more of these applications get integrated into aerospace and defense use cases, the security of the communication channel between the ground station and the mobile agent is of increasing importance. The development of quantum computing devices poses a unique threat to secure communications due to the vulnerability of asymmetric ciphers to Shor's algorithm. Given the active development of new quantum resistant encryption techniques, we report the first integration of post-quantum secure encryption schemes with the robot operating system (ROS) and C&C of mobile agents, in general. We integrate these schemes in the application and network layers, and study the performance of these methods by comparing them to present day security schemes such as the widely used RSA algorithm.

Estimating the Density of States of Boolean Satisfiability Problems on Classical and Quantum Computing Platforms

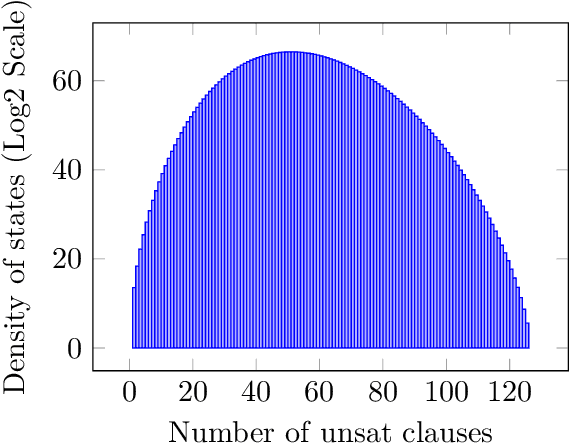
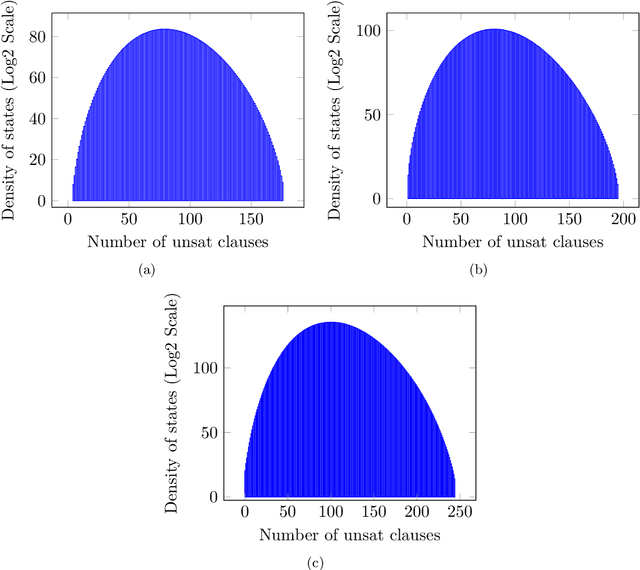
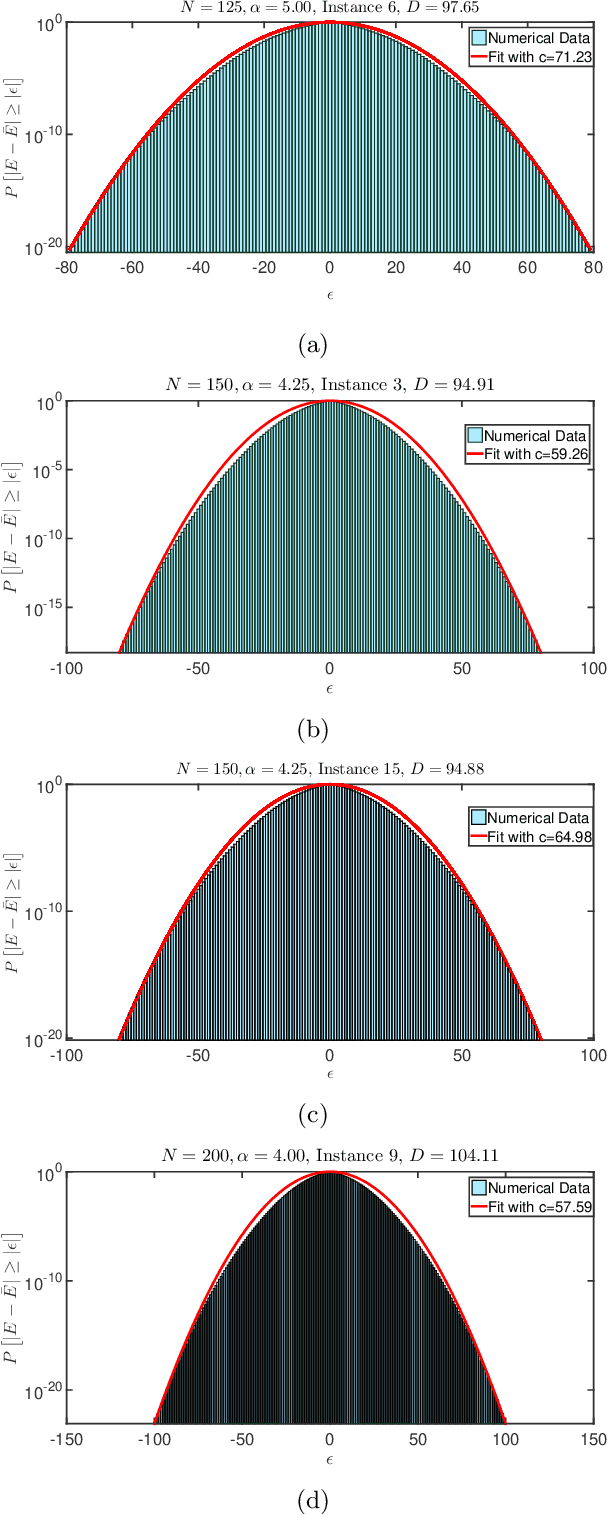
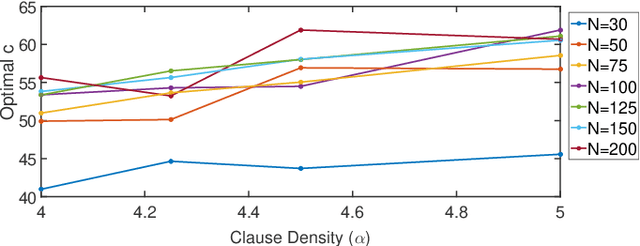
Given a Boolean formula $\phi(x)$ in conjunctive normal form (CNF), the density of states counts the number of variable assignments that violate exactly $e$ clauses, for all values of $e$. Thus, the density of states is a histogram of the number of unsatisfied clauses over all possible assignments. This computation generalizes both maximum-satisfiability (MAX-SAT) and model counting problems and not only provides insight into the entire solution space, but also yields a measure for the \emph{hardness} of the problem instance. Consequently, in real-world scenarios, this problem is typically infeasible even when using state-of-the-art algorithms. While finding an exact answer to this problem is a computationally intensive task, we propose a novel approach for estimating density of states based on the concentration of measure inequalities. The methodology results in a quadratic unconstrained binary optimization (QUBO), which is particularly amenable to quantum annealing-based solutions. We present the overall approach and compare results from the D-Wave quantum annealer against the best-known classical algorithms such as the Hamze-de Freitas-Selby (HFS) algorithm and satisfiability modulo theory (SMT) solvers.

A Chaotic Dynamical System that Paints

Can a dynamical system paint masterpieces such as Da Vinci's Mona Lisa or Monet's Water Lilies? Moreover, can this dynamical system be chaotic in the sense that although the trajectories are sensitive to initial conditions, the same painting is created every time? Setting aside the creative aspect of painting a picture, in this work, we develop a novel algorithm to reproduce paintings and photographs. Combining ideas from ergodic theory and control theory, we construct a chaotic dynamical system with predetermined statistical properties. If one makes the spatial distribution of colors in the picture the target distribution, akin to a human, the algorithm first captures large scale features and then goes on to refine small scale features. Beyond reproducing paintings, this approach is expected to have a wide variety of applications such as uncertainty quantification, sampling for efficient inference in scalable machine learning for big data, and developing effective strategies for search and rescue. In particular, our preliminary studies demonstrate that this algorithm provides significant acceleration and higher accuracy than competing methods for Markov Chain Monte Carlo (MCMC).

A Traveling Salesman Learns Bayesian Networks

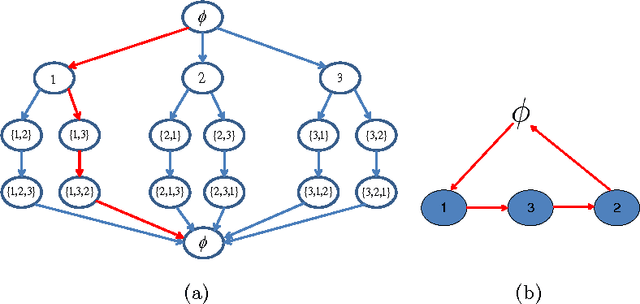
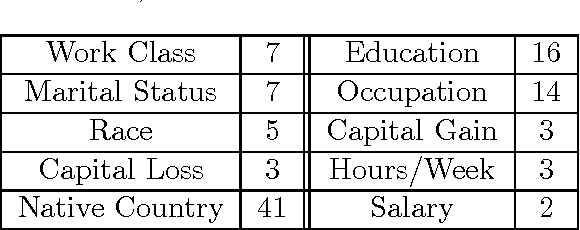
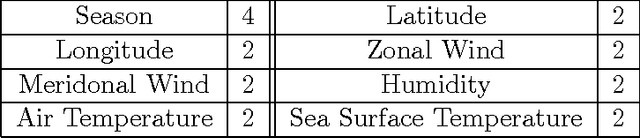
Structure learning of Bayesian networks is an important problem that arises in numerous machine learning applications. In this work, we present a novel approach for learning the structure of Bayesian networks using the solution of an appropriately constructed traveling salesman problem. In our approach, one computes an optimal ordering (partially ordered set) of random variables using methods for the traveling salesman problem. This ordering significantly reduces the search space for the subsequent greedy optimization that computes the final structure of the Bayesian network. We demonstrate our approach of learning Bayesian networks on real world census and weather datasets. In both cases, we demonstrate that the approach very accurately captures dependencies between random variables. We check the accuracy of the predictions based on independent studies in both application domains.