Estimating the Density of States of Boolean Satisfiability Problems on Classical and Quantum Computing Platforms
Paper and Code
Oct 29, 2019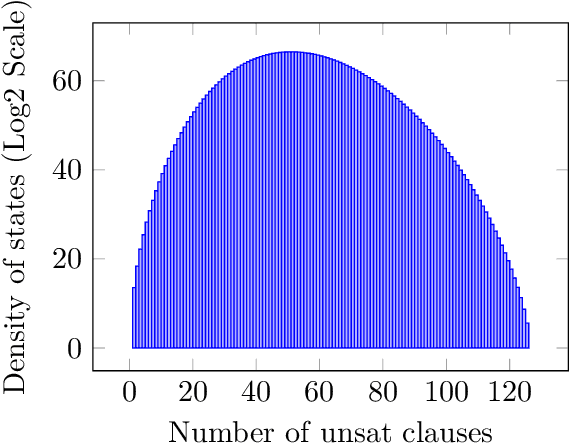
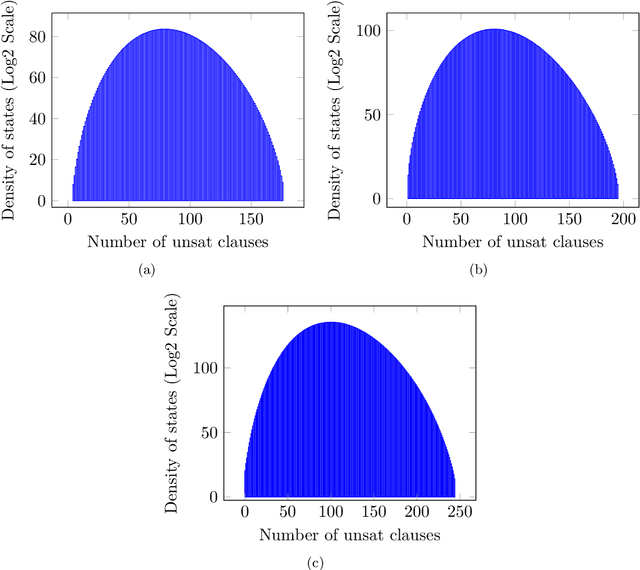
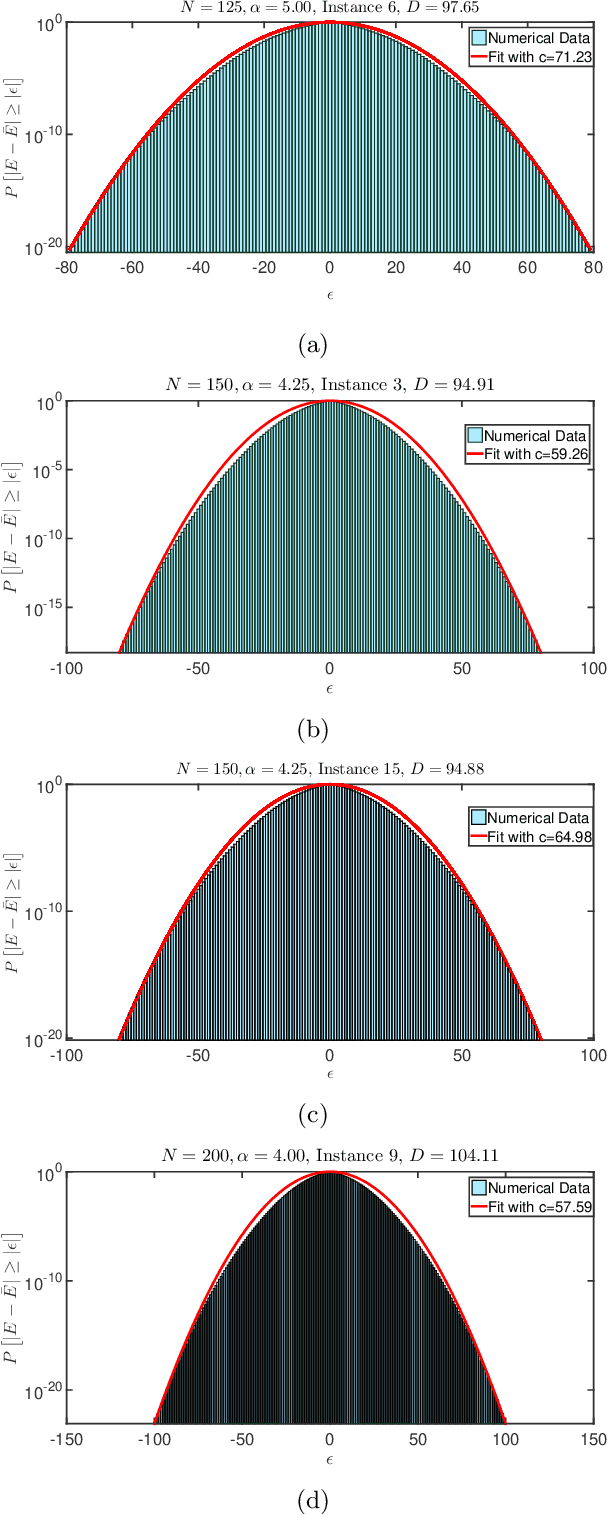
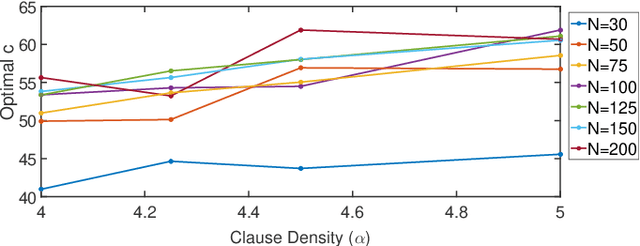
Given a Boolean formula $\phi(x)$ in conjunctive normal form (CNF), the density of states counts the number of variable assignments that violate exactly $e$ clauses, for all values of $e$. Thus, the density of states is a histogram of the number of unsatisfied clauses over all possible assignments. This computation generalizes both maximum-satisfiability (MAX-SAT) and model counting problems and not only provides insight into the entire solution space, but also yields a measure for the \emph{hardness} of the problem instance. Consequently, in real-world scenarios, this problem is typically infeasible even when using state-of-the-art algorithms. While finding an exact answer to this problem is a computationally intensive task, we propose a novel approach for estimating density of states based on the concentration of measure inequalities. The methodology results in a quadratic unconstrained binary optimization (QUBO), which is particularly amenable to quantum annealing-based solutions. We present the overall approach and compare results from the D-Wave quantum annealer against the best-known classical algorithms such as the Hamze-de Freitas-Selby (HFS) algorithm and satisfiability modulo theory (SMT) solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge