Error Estimation for Physics-informed Neural Networks Approximating Semilinear Wave Equations

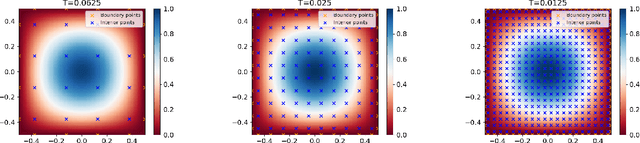
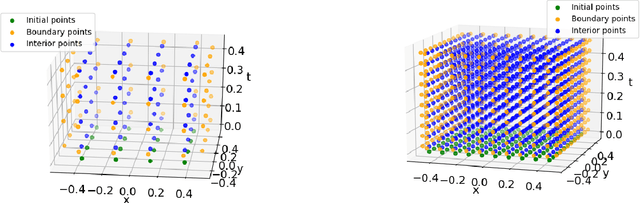
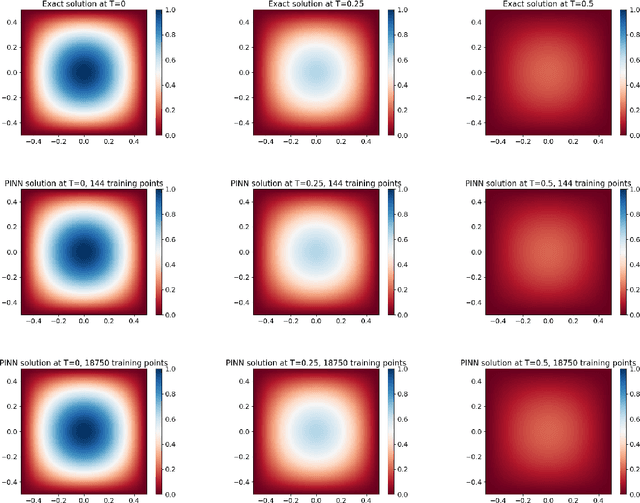
This paper provides rigorous error bounds for physics-informed neural networks approximating the semilinear wave equation. We provide bounds for the generalization and training error in terms of the width of the network's layers and the number of training points for a tanh neural network with two hidden layers. Our main result is a bound of the total error in the $H^1([0,T];L^2(\Omega))$-norm in terms of the training error and the number of training points, which can be made arbitrarily small under some assumptions. We illustrate our theoretical bounds with numerical experiments.

Learning-based adaption of robotic friction models

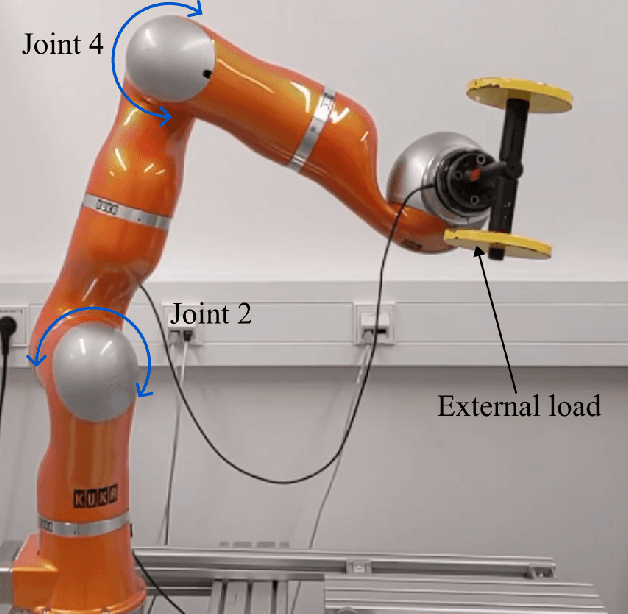
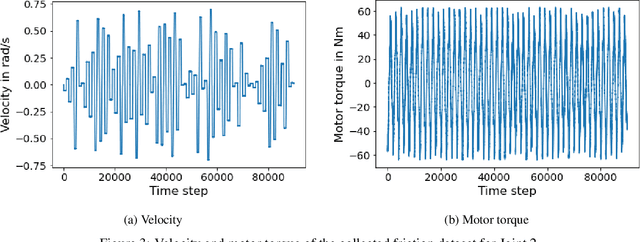
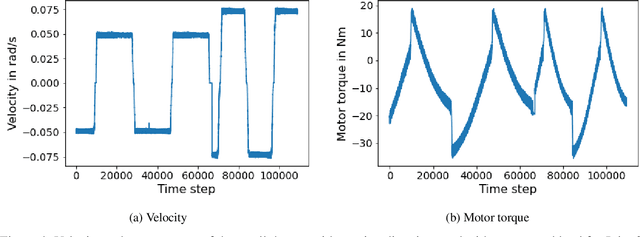
In the Fourth Industrial Revolution, wherein artificial intelligence and the automation of machines occupy a central role, the deployment of robots is indispensable. However, the manufacturing process using robots, especially in collaboration with humans, is highly intricate. In particular, modeling the friction torque in robotic joints is a longstanding problem due to the lack of a good mathematical description. This motivates the usage of data-driven methods in recent works. However, model-based and data-driven models often exhibit limitations in their ability to generalize beyond the specific dynamics they were trained on, as we demonstrate in this paper. To address this challenge, we introduce a novel approach based on residual learning, which aims to adapt an existing friction model to new dynamics using as little data as possible. We validate our approach by training a base neural network on a symmetric friction data set to learn an accurate relation between the velocity and the friction torque. Subsequently, to adapt to more complex asymmetric settings, we train a second network on a small dataset, focusing on predicting the residual of the initial network's output. By combining the output of both networks in a suitable manner, our proposed estimator outperforms the conventional model-based approach and the base neural network significantly. Furthermore, we evaluate our method on trajectories involving external loads and still observe a substantial improvement, approximately 60-70\%, over the conventional approach. Our method does not rely on data with external load during training, eliminating the need for external torque sensors. This demonstrates the generalization capability of our approach, even with a small amount of data-only 43 seconds of a robot movement-enabling adaptation to diverse scenarios based on prior knowledge about friction in different settings.

PoissonNet: Resolution-Agnostic 3D Shape Reconstruction using Fourier Neural Operators

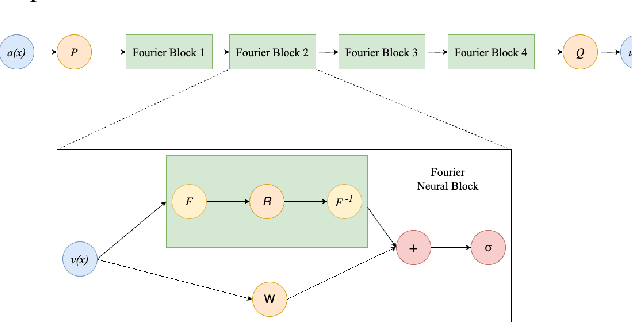
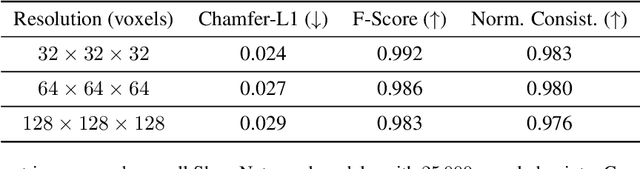
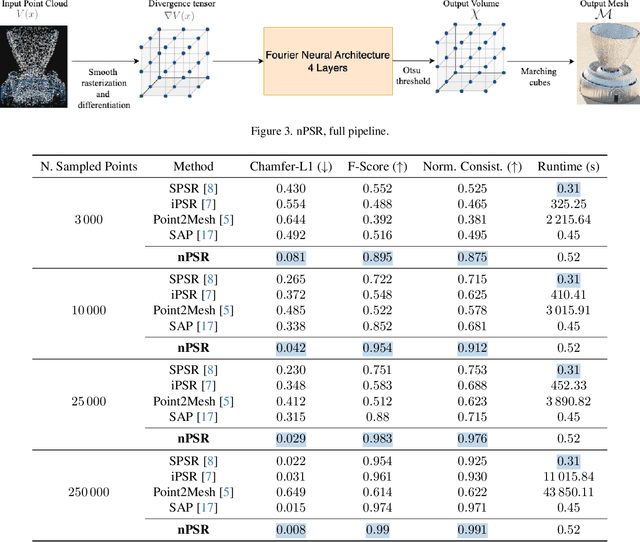
We introduce PoissonNet, an architecture for shape reconstruction that addresses the challenge of recovering 3D shapes from points. Traditional deep neural networks face challenges with common 3D shape discretization techniques due to their computational complexity at higher resolutions. To overcome this, we leverage Fourier Neural Operators (FNOs) to solve the Poisson equation and reconstruct a mesh from oriented point cloud measurements. PoissonNet exhibits two main advantages. First, it enables efficient training on low-resolution data while achieving comparable performance at high-resolution evaluation, thanks to the resolution-agnostic nature of FNOs. This feature allows for one-shot super-resolution. Second, our method surpasses existing approaches in reconstruction quality while being differentiable. Overall, our proposed method not only improves upon the limitations of classical deep neural networks in shape reconstruction but also achieves superior results in terms of reconstruction quality, running time, and resolution flexibility. Furthermore, we demonstrate that the Poisson surface reconstruction problem is well-posed in the limit case by showing a universal approximation theorem for the solution operator of the Poisson equation with distributional data utilizing the Fourier Neural Operator, which provides a theoretical foundation for our numerical results. The code to reproduce the experiments is available on: \url{https://github.com/arsenal9971/PoissonNet}.

Reliable AI: Does the Next Generation Require Quantum Computing?

In this survey, we aim to explore the fundamental question of whether the next generation of artificial intelligence requires quantum computing. Artificial intelligence is increasingly playing a crucial role in many aspects of our daily lives and is central to the fourth industrial revolution. It is therefore imperative that artificial intelligence is reliable and trustworthy. However, there are still many issues with reliability of artificial intelligence, such as privacy, responsibility, safety, and security, in areas such as autonomous driving, healthcare, robotics, and others. These problems can have various causes, including insufficient data, biases, and robustness problems, as well as fundamental issues such as computability problems on digital hardware. The cause of these computability problems is rooted in the fact that digital hardware is based on the computing model of the Turing machine, which is inherently discrete. Notably, our findings demonstrate that digital hardware is inherently constrained in solving problems about optimization, deep learning, or differential equations. Therefore, these limitations carry substantial implications for the field of artificial intelligence, in particular for machine learning. Furthermore, although it is well known that the quantum computer shows a quantum advantage for certain classes of problems, our findings establish that some of these limitations persist when employing quantum computing models based on the quantum circuit or the quantum Turing machine paradigm. In contrast, analog computing models, such as the Blum-Shub-Smale machine, exhibit the potential to surmount these limitations.

A Fractional Graph Laplacian Approach to Oversmoothing

Graph neural networks (GNNs) have shown state-of-the-art performances in various applications. However, GNNs often struggle to capture long-range dependencies in graphs due to oversmoothing. In this paper, we generalize the concept of oversmoothing from undirected to directed graphs. To this aim, we extend the notion of Dirichlet energy by considering a directed symmetrically normalized Laplacian. As vanilla graph convolutional networks are prone to oversmooth, we adopt a neural graph ODE framework. Specifically, we propose fractional graph Laplacian neural ODEs, which describe non-local dynamics. We prove that our approach allows propagating information between distant nodes while maintaining a low probability of long-distance jumps. Moreover, we show that our method is more flexible with respect to the convergence of the graph's Dirichlet energy, thereby mitigating oversmoothing. We conduct extensive experiments on synthetic and real-world graphs, both directed and undirected, demonstrating our method's versatility across diverse graph homophily levels. Our code is available at https://github.com/RPaolino/fLode .

Well-definedness of Physical Law Learning: The Uniqueness Problem

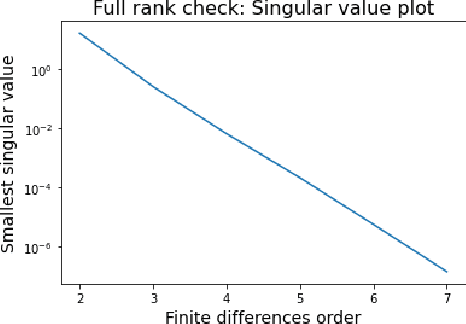
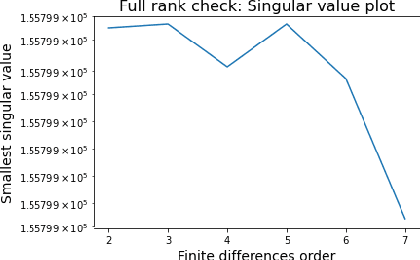
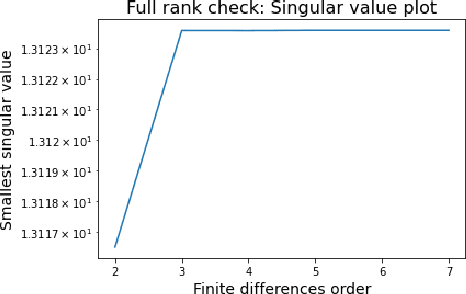
Physical law learning is the ambiguous attempt at automating the derivation of governing equations with the use of machine learning techniques. The current literature focuses however solely on the development of methods to achieve this goal, and a theoretical foundation is at present missing. This paper shall thus serve as a first step to build a comprehensive theoretical framework for learning physical laws, aiming to provide reliability to according algorithms. One key problem consists in the fact that the governing equations might not be uniquely determined by the given data. We will study this problem in the common situation of having a physical law be described by an ordinary or partial differential equation. For various different classes of differential equations, we provide both necessary and sufficient conditions for a function from a given function class to uniquely determine the differential equation which is governing the phenomenon. We then use our results to devise numerical algorithms to determine whether a function solves a differential equation uniquely. Finally, we provide extensive numerical experiments showing that our algorithms in combination with common approaches for learning physical laws indeed allow to guarantee that a unique governing differential equation is learnt, without assuming any knowledge about the function, thereby ensuring reliability.