Julius Hege
PoissonNet: Resolution-Agnostic 3D Shape Reconstruction using Fourier Neural Operators
Aug 04, 2023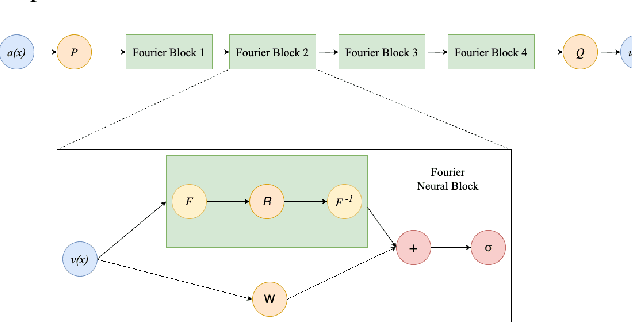
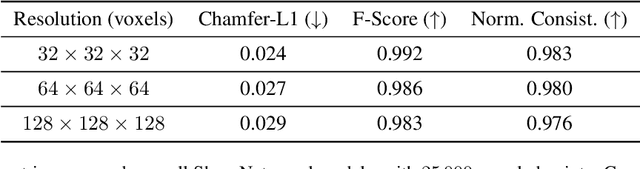
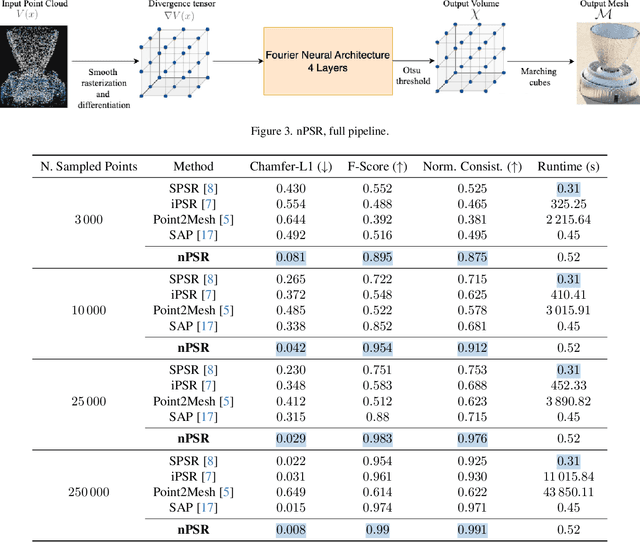

Abstract:We introduce PoissonNet, an architecture for shape reconstruction that addresses the challenge of recovering 3D shapes from points. Traditional deep neural networks face challenges with common 3D shape discretization techniques due to their computational complexity at higher resolutions. To overcome this, we leverage Fourier Neural Operators (FNOs) to solve the Poisson equation and reconstruct a mesh from oriented point cloud measurements. PoissonNet exhibits two main advantages. First, it enables efficient training on low-resolution data while achieving comparable performance at high-resolution evaluation, thanks to the resolution-agnostic nature of FNOs. This feature allows for one-shot super-resolution. Second, our method surpasses existing approaches in reconstruction quality while being differentiable. Overall, our proposed method not only improves upon the limitations of classical deep neural networks in shape reconstruction but also achieves superior results in terms of reconstruction quality, running time, and resolution flexibility. Furthermore, we demonstrate that the Poisson surface reconstruction problem is well-posed in the limit case by showing a universal approximation theorem for the solution operator of the Poisson equation with distributional data utilizing the Fourier Neural Operator, which provides a theoretical foundation for our numerical results. The code to reproduce the experiments is available on: \url{https://github.com/arsenal9971/PoissonNet}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge