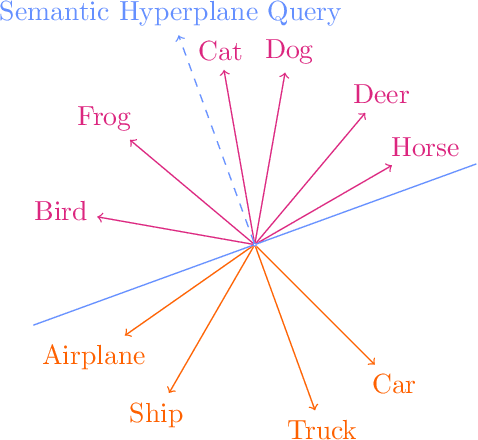
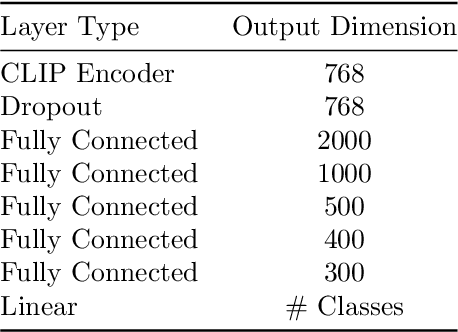
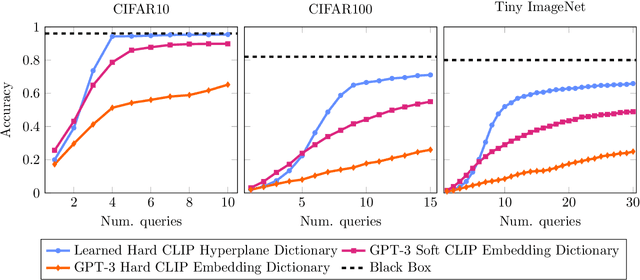
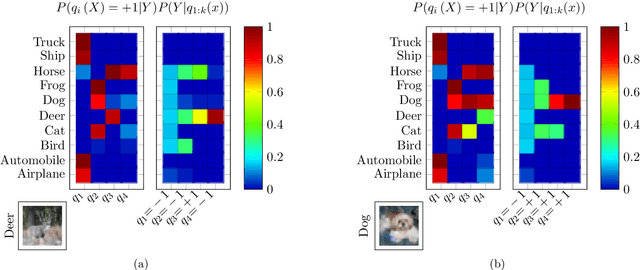
Learning Interpretable Queries for Explainable Image Classification with Information Pursuit

Information Pursuit (IP) is an explainable prediction algorithm that greedily selects a sequence of interpretable queries about the data in order of information gain, updating its posterior at each step based on observed query-answer pairs. The standard paradigm uses hand-crafted dictionaries of potential data queries curated by a domain expert or a large language model after a human prompt. However, in practice, hand-crafted dictionaries are limited by the expertise of the curator and the heuristics of prompt engineering. This paper introduces a novel approach: learning a dictionary of interpretable queries directly from the dataset. Our query dictionary learning problem is formulated as an optimization problem by augmenting IP's variational formulation with learnable dictionary parameters. To formulate learnable and interpretable queries, we leverage the latent space of large vision and language models like CLIP. To solve the optimization problem, we propose a new query dictionary learning algorithm inspired by classical sparse dictionary learning. Our experiments demonstrate that learned dictionaries significantly outperform hand-crafted dictionaries generated with large language models.

PoissonNet: Resolution-Agnostic 3D Shape Reconstruction using Fourier Neural Operators

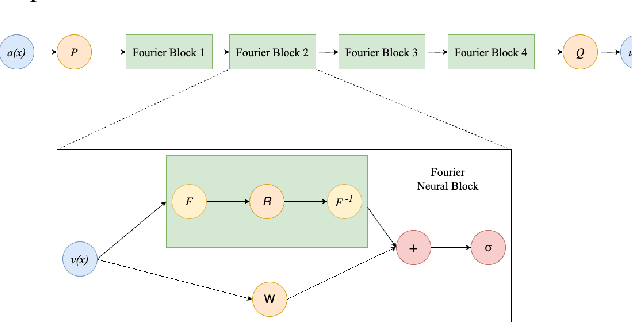
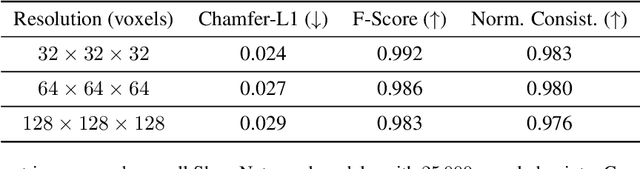
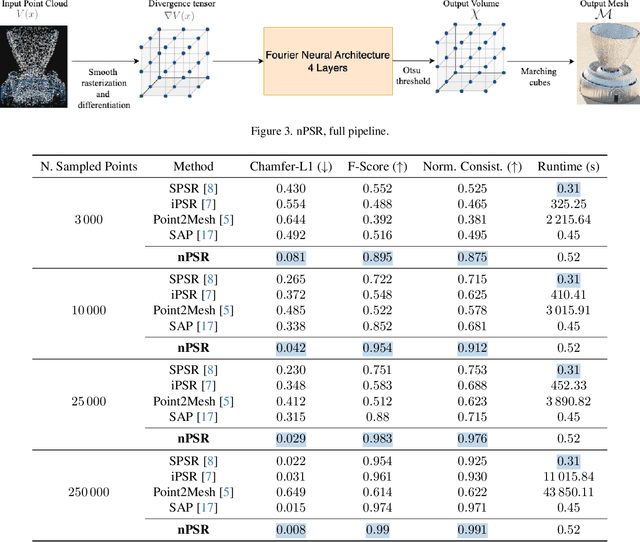
We introduce PoissonNet, an architecture for shape reconstruction that addresses the challenge of recovering 3D shapes from points. Traditional deep neural networks face challenges with common 3D shape discretization techniques due to their computational complexity at higher resolutions. To overcome this, we leverage Fourier Neural Operators (FNOs) to solve the Poisson equation and reconstruct a mesh from oriented point cloud measurements. PoissonNet exhibits two main advantages. First, it enables efficient training on low-resolution data while achieving comparable performance at high-resolution evaluation, thanks to the resolution-agnostic nature of FNOs. This feature allows for one-shot super-resolution. Second, our method surpasses existing approaches in reconstruction quality while being differentiable. Overall, our proposed method not only improves upon the limitations of classical deep neural networks in shape reconstruction but also achieves superior results in terms of reconstruction quality, running time, and resolution flexibility. Furthermore, we demonstrate that the Poisson surface reconstruction problem is well-posed in the limit case by showing a universal approximation theorem for the solution operator of the Poisson equation with distributional data utilizing the Fourier Neural Operator, which provides a theoretical foundation for our numerical results. The code to reproduce the experiments is available on: \url{https://github.com/arsenal9971/PoissonNet}.