Mariia Seleznova
Latent Structure Emergence in Diffusion Models via Confidence-Based Filtering
Feb 05, 2026Abstract:Diffusion models rely on a high-dimensional latent space of initial noise seeds, yet it remains unclear whether this space contains sufficient structure to predict properties of the generated samples, such as their classes. In this work, we investigate the emergence of latent structure through the lens of confidence scores assigned by a pre-trained classifier to generated samples. We show that while the latent space appears largely unstructured when considering all noise realizations, restricting attention to initial noise seeds that produce high-confidence samples reveals pronounced class separability. By comparing class predictability across noise subsets of varying confidence and examining the class separability of the latent space, we find evidence of class-relevant latent structure that becomes observable only under confidence-based filtering. As a practical implication, we discuss how confidence-based filtering enables conditional generation as an alternative to guidance-based methods.
Revisiting Glorot Initialization for Long-Range Linear Recurrences
May 26, 2025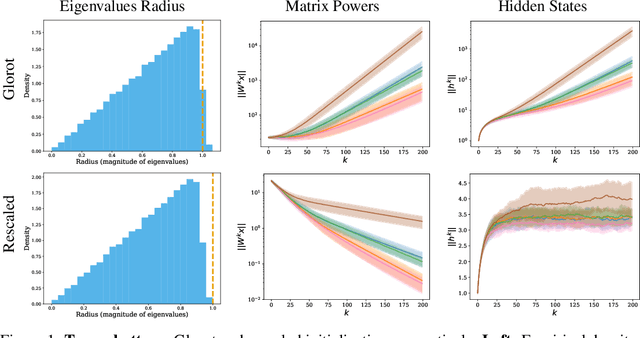
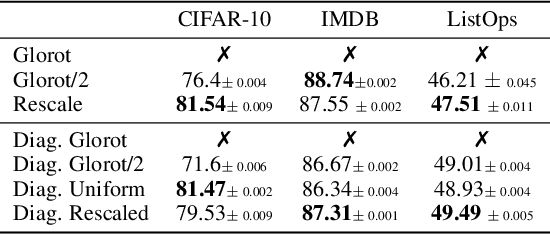
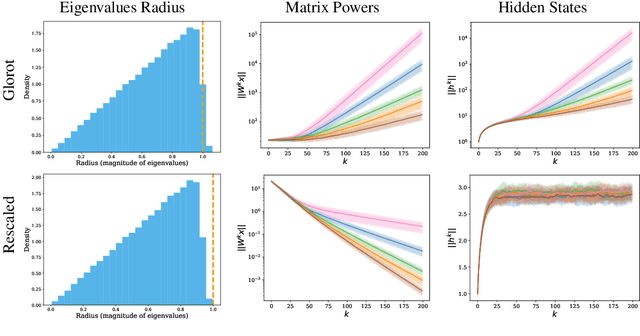
Abstract:Proper initialization is critical for Recurrent Neural Networks (RNNs), particularly in long-range reasoning tasks, where repeated application of the same weight matrix can cause vanishing or exploding signals. A common baseline for linear recurrences is Glorot initialization, designed to ensure stable signal propagation--but derived under the infinite-width, fixed-length regime--an unrealistic setting for RNNs processing long sequences. In this work, we show that Glorot initialization is in fact unstable: small positive deviations in the spectral radius are amplified through time and cause the hidden state to explode. Our theoretical analysis demonstrates that sequences of length $t = O(\sqrt{n})$, where $n$ is the hidden width, are sufficient to induce instability. To address this, we propose a simple, dimension-aware rescaling of Glorot that shifts the spectral radius slightly below one, preventing rapid signal explosion or decay. These results suggest that standard initialization schemes may break down in the long-sequence regime, motivating a separate line of theory for stable recurrent initialization.
GradPCA: Leveraging NTK Alignment for Reliable Out-of-Distribution Detection
May 21, 2025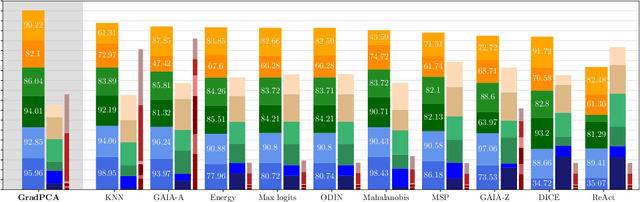
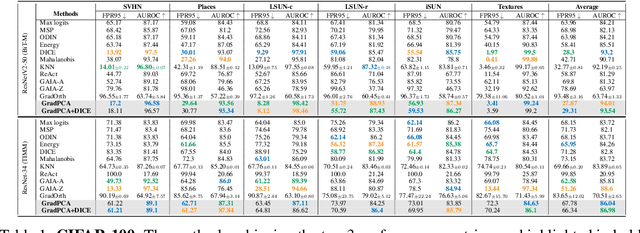

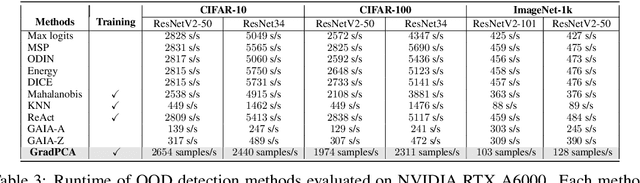
Abstract:We introduce GradPCA, an Out-of-Distribution (OOD) detection method that exploits the low-rank structure of neural network gradients induced by Neural Tangent Kernel (NTK) alignment. GradPCA applies Principal Component Analysis (PCA) to gradient class-means, achieving more consistent performance than existing methods across standard image classification benchmarks. We provide a theoretical perspective on spectral OOD detection in neural networks to support GradPCA, highlighting feature-space properties that enable effective detection and naturally emerge from NTK alignment. Our analysis further reveals that feature quality -- particularly the use of pretrained versus non-pretrained representations -- plays a crucial role in determining which detectors will succeed. Extensive experiments validate the strong performance of GradPCA, and our theoretical framework offers guidance for designing more principled spectral OOD detectors.
Neural (Tangent Kernel) Collapse
May 25, 2023Abstract:This work bridges two important concepts: the Neural Tangent Kernel (NTK), which captures the evolution of deep neural networks (DNNs) during training, and the Neural Collapse (NC) phenomenon, which refers to the emergence of symmetry and structure in the last-layer features of well-trained classification DNNs. We adopt the natural assumption that the empirical NTK develops a block structure aligned with the class labels, i.e., samples within the same class have stronger correlations than samples from different classes. Under this assumption, we derive the dynamics of DNNs trained with mean squared (MSE) loss and break them into interpretable phases. Moreover, we identify an invariant that captures the essence of the dynamics, and use it to prove the emergence of NC in DNNs with block-structured NTK. We provide large-scale numerical experiments on three common DNN architectures and three benchmark datasets to support our theory.
Neural Tangent Kernel Beyond the Infinite-Width Limit: Effects of Depth and Initialization
Feb 01, 2022



Abstract:Neural Tangent Kernel (NTK) is widely used to analyze overparametrized neural networks due to the famous result by (Jacot et al., 2018): in the infinite-width limit, the NTK is deterministic and constant during training. However, this result cannot explain the behavior of deep networks, since it generally does not hold if depth and width tend to infinity simultaneously. In this paper, we study the NTK of fully-connected ReLU networks with depth comparable to width. We prove that the NTK properties depend significantly on the depth-to-width ratio and the distribution of parameters at initialization. In fact, our results indicate the importance of the three phases in the hyperparameter space identified in (Poole et al., 2016): ordered, chaotic and the edge of chaos (EOC). We derive exact expressions for the NTK dispersion in the infinite-depth-and-width limit in all three phases and conclude that the NTK variability grows exponentially with depth at the EOC and in the chaotic phase but not in the ordered phase. We also show that the NTK of deep networks may stay constant during training only in the ordered phase and discuss how the structure of the NTK matrix changes during training.
Analyzing Finite Neural Networks: Can We Trust Neural Tangent Kernel Theory?
Dec 08, 2020



Abstract:Neural Tangent Kernel (NTK) theory is widely used to study the dynamics of infinitely-wide deep neural networks (DNNs) under gradient descent. But do the results for infinitely-wide networks give us hints about the behaviour of real finite-width ones? In this paper we study empirically when NTK theory is valid in practice for fully-connected ReLu and sigmoid networks. We find out that whether a network is in the NTK regime depends on the hyperparameters of random initialization and network's depth. In particular, NTK theory does not explain behaviour of sufficiently deep networks initialized so that their gradients explode: the kernel is random at initialization and changes significantly during training, contrary to NTK theory. On the other hand, in case of vanishing gradients DNNs are in the NTK regime but become untrainable rapidly with depth. We also describe a framework to study generalization properties of DNNs by means of NTK theory and discuss its limits.
Towards Large-Scale Exploratory Search over Heterogeneous Sources
Nov 20, 2018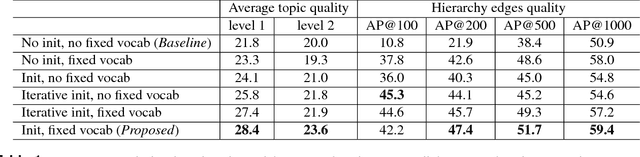
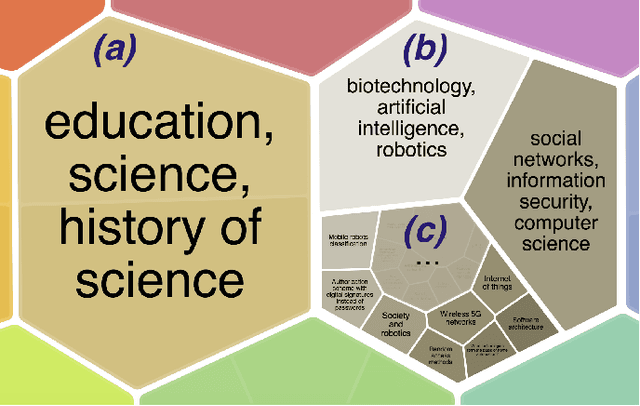

Abstract:Since time immemorial, people have been looking for ways to organize scientific knowledge into some systems to facilitate search and discovery of new ideas. The problem was partially solved in the pre-Internet era using library classifications, but nowadays it is nearly impossible to classify all scientific and popular scientific knowledge manually. There is a clear gap between the diversity and the amount of data available on the Internet and the algorithms for automatic structuring of such data. In our preliminary study, we approach the problem of knowledge discovery on web-scale data with diverse text sources and propose an algorithm to aggregate multiple collections into a single hierarchical topic model. We implement a web service named Rysearch to demonstrate the concept of topical exploratory search and make it available online.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge