Noga Bar
Revisiting Glorot Initialization for Long-Range Linear Recurrences
May 26, 2025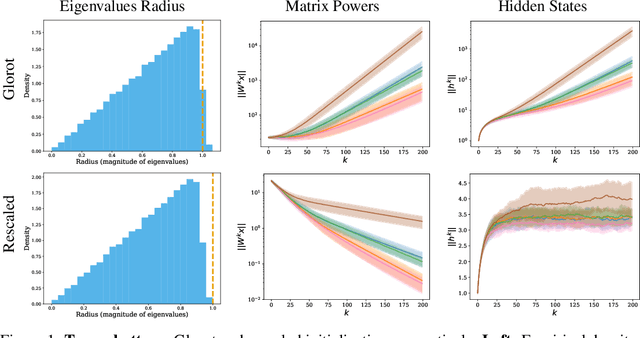
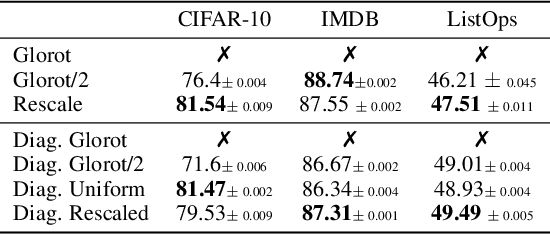
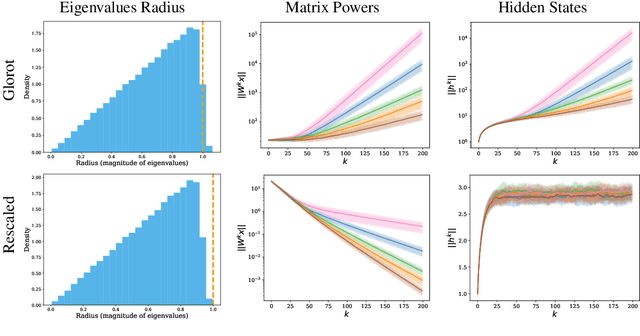
Abstract:Proper initialization is critical for Recurrent Neural Networks (RNNs), particularly in long-range reasoning tasks, where repeated application of the same weight matrix can cause vanishing or exploding signals. A common baseline for linear recurrences is Glorot initialization, designed to ensure stable signal propagation--but derived under the infinite-width, fixed-length regime--an unrealistic setting for RNNs processing long sequences. In this work, we show that Glorot initialization is in fact unstable: small positive deviations in the spectral radius are amplified through time and cause the hidden state to explode. Our theoretical analysis demonstrates that sequences of length $t = O(\sqrt{n})$, where $n$ is the hidden width, are sufficient to induce instability. To address this, we propose a simple, dimension-aware rescaling of Glorot that shifts the spectral radius slightly below one, preventing rapid signal explosion or decay. These results suggest that standard initialization schemes may break down in the long-sequence regime, motivating a separate line of theory for stable recurrent initialization.
ZOQO: Zero-Order Quantized Optimization
Jan 12, 2025


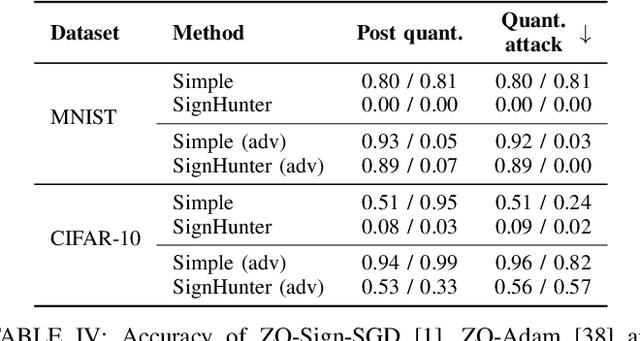
Abstract:The increasing computational and memory demands in deep learning present significant challenges, especially in resource-constrained environments. We introduce a zero-order quantized optimization (ZOQO) method designed for training models with quantized parameters and operations. Our approach leverages zero-order approximations of the gradient sign and adapts the learning process to maintain the parameters' quantization without the need for full-precision gradient calculations. We demonstrate the effectiveness of ZOQO through experiments in fine-tuning of large language models and black-box adversarial attacks. Despite the limitations of zero-order and quantized operations training, our method achieves competitive performance compared to full-precision methods, highlighting its potential for low-resource environments.
Effective Subset Selection Through The Lens of Neural Network Pruning
Jun 03, 2024Abstract:Having large amounts of annotated data significantly impacts the effectiveness of deep neural networks. However, the annotation task can be very expensive in some domains, such as medical data. Thus, it is important to select the data to be annotated wisely, which is known as the subset selection problem. We investigate the relationship between subset selection and neural network pruning, which is more widely studied, and establish a correspondence between them. Leveraging insights from network pruning, we propose utilizing the norm criterion of neural network features to improve subset selection methods. We empirically validate our proposed strategy on various networks and datasets, demonstrating enhanced accuracy. This shows the potential of employing pruning tools for subset selection.
Group Orthogonalization Regularization For Vision Models Adaptation and Robustness
Jun 16, 2023Abstract:As neural networks become deeper, the redundancy within their parameters increases. This phenomenon has led to several methods that attempt to reduce the correlation between convolutional filters. We propose a computationally efficient regularization technique that encourages orthonormality between groups of filters within the same layer. Our experiments show that when incorporated into recent adaptation methods for diffusion models and vision transformers (ViTs), this regularization improves performance on downstream tasks. We further show improved robustness when group orthogonality is enforced during adversarial training. Our code is available at https://github.com/YoavKurtz/GOR.
Pruning at Initialization -- A Sketching Perspective
May 27, 2023Abstract:The lottery ticket hypothesis (LTH) has increased attention to pruning neural networks at initialization. We study this problem in the linear setting. We show that finding a sparse mask at initialization is equivalent to the sketching problem introduced for efficient matrix multiplication. This gives us tools to analyze the LTH problem and gain insights into it. Specifically, using the mask found at initialization, we bound the approximation error of the pruned linear model at the end of training. We theoretically justify previous empirical evidence that the search for sparse networks may be data independent. By using the sketching perspective, we suggest a generic improvement to existing algorithms for pruning at initialization, which we show to be beneficial in the data-independent case.
Multiplicative Reweighting for Robust Neural Network Optimization
Feb 24, 2021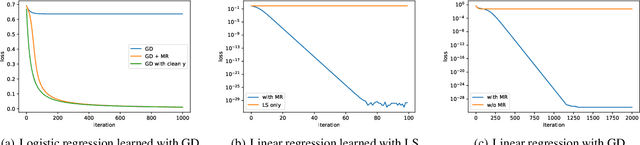
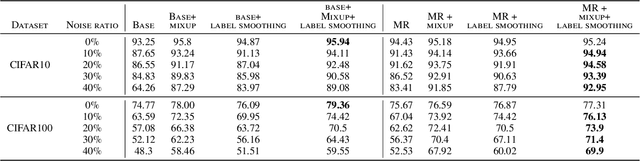
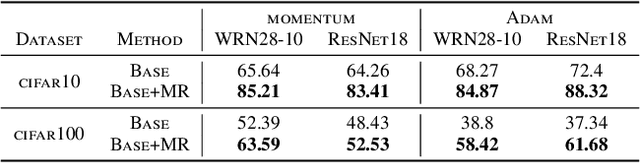
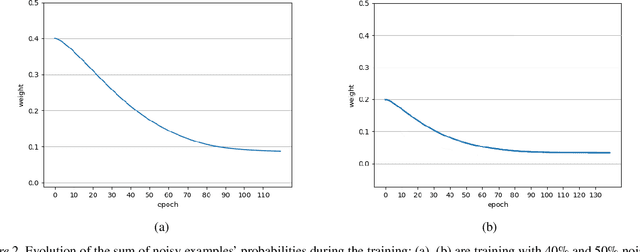
Abstract:Deep neural networks are widespread due to their powerful performance. Yet, they suffer from degraded performance in the presence of noisy labels at train time or adversarial examples during inference. Inspired by the setting of learning with expert advice, where multiplicative weights (MW) updates were recently shown to be robust to moderate adversarial corruptions, we propose to use MW for reweighting examples during neural networks optimization. We establish the convergence of our method when used with gradient descent and demonstrate its advantage in two simple examples. We then validate empirically our findings by showing that MW improves network's accuracy in the presence of label noise on CIFAR-10, CIFAR-100 and Clothing1M, and that it leads to better robustness to adversarial attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge