Conflicting Biases at the Edge of Stability: Norm versus Sharpness Regularization

A widely believed explanation for the remarkable generalization capacities of overparameterized neural networks is that the optimization algorithms used for training induce an implicit bias towards benign solutions. To grasp this theoretically, recent works examine gradient descent and its variants in simplified training settings, often assuming vanishing learning rates. These studies reveal various forms of implicit regularization, such as $\ell_1$-norm minimizing parameters in regression and max-margin solutions in classification. Concurrently, empirical findings show that moderate to large learning rates exceeding standard stability thresholds lead to faster, albeit oscillatory, convergence in the so-called Edge-of-Stability regime, and induce an implicit bias towards minima of low sharpness (norm of training loss Hessian). In this work, we argue that a comprehensive understanding of the generalization performance of gradient descent requires analyzing the interaction between these various forms of implicit regularization. We empirically demonstrate that the learning rate balances between low parameter norm and low sharpness of the trained model. We furthermore prove for diagonal linear networks trained on a simple regression task that neither implicit bias alone minimizes the generalization error. These findings demonstrate that focusing on a single implicit bias is insufficient to explain good generalization, and they motivate a broader view of implicit regularization that captures the dynamic trade-off between norm and sharpness induced by non-negligible learning rates.

GradPCA: Leveraging NTK Alignment for Reliable Out-of-Distribution Detection

We introduce GradPCA, an Out-of-Distribution (OOD) detection method that exploits the low-rank structure of neural network gradients induced by Neural Tangent Kernel (NTK) alignment. GradPCA applies Principal Component Analysis (PCA) to gradient class-means, achieving more consistent performance than existing methods across standard image classification benchmarks. We provide a theoretical perspective on spectral OOD detection in neural networks to support GradPCA, highlighting feature-space properties that enable effective detection and naturally emerge from NTK alignment. Our analysis further reveals that feature quality -- particularly the use of pretrained versus non-pretrained representations -- plays a crucial role in determining which detectors will succeed. Extensive experiments validate the strong performance of GradPCA, and our theoretical framework offers guidance for designing more principled spectral OOD detectors.

Neural (Tangent Kernel) Collapse

This work bridges two important concepts: the Neural Tangent Kernel (NTK), which captures the evolution of deep neural networks (DNNs) during training, and the Neural Collapse (NC) phenomenon, which refers to the emergence of symmetry and structure in the last-layer features of well-trained classification DNNs. We adopt the natural assumption that the empirical NTK develops a block structure aligned with the class labels, i.e., samples within the same class have stronger correlations than samples from different classes. Under this assumption, we derive the dynamics of DNNs trained with mean squared (MSE) loss and break them into interpretable phases. Moreover, we identify an invariant that captures the essence of the dynamics, and use it to prove the emergence of NC in DNNs with block-structured NTK. We provide large-scale numerical experiments on three common DNN architectures and three benchmark datasets to support our theory.

Robust Implicit Regularization via Weight Normalization

Overparameterized models may have many interpolating solutions; implicit regularization refers to the hidden preference of a particular optimization method towards a certain interpolating solution among the many. A by now established line of work has shown that (stochastic) gradient descent tends to have an implicit bias towards low rank and/or sparse solutions when used to train deep linear networks, explaining to some extent why overparameterized neural network models trained by gradient descent tend to have good generalization performance in practice. However, existing theory for square-loss objectives often requires very small initialization of the trainable weights, which is at odds with the larger scale at which weights are initialized in practice for faster convergence and better generalization performance. In this paper, we aim to close this gap by incorporating and analyzing gradient descent with weight normalization, where the weight vector is reparamterized in terms of polar coordinates, and gradient descent is applied to the polar coordinates. By analyzing key invariants of the gradient flow and using Lojasiewicz's Theorem, we show that weight normalization also has an implicit bias towards sparse solutions in the diagonal linear model, but that in contrast to plain gradient descent, weight normalization enables a robust bias that persists even if the weights are initialized at practically large scale. Experiments suggest that the gains in both convergence speed and robustness of the implicit bias are improved dramatically by using weight normalization in overparameterized diagonal linear network models.

More is Less: Inducing Sparsity via Overparameterization

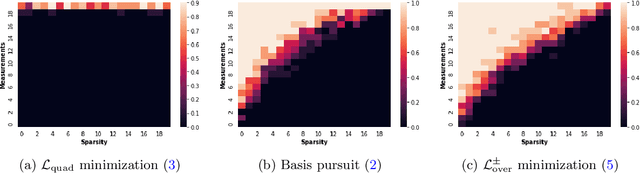
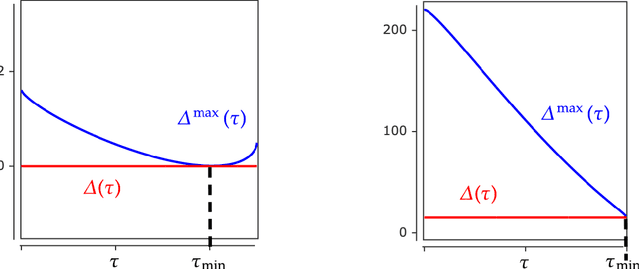
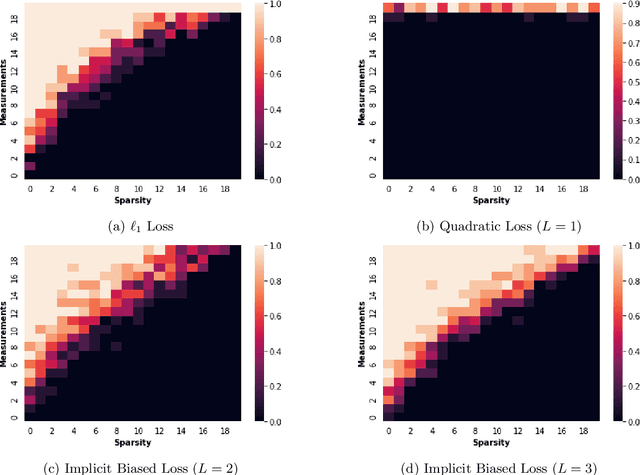
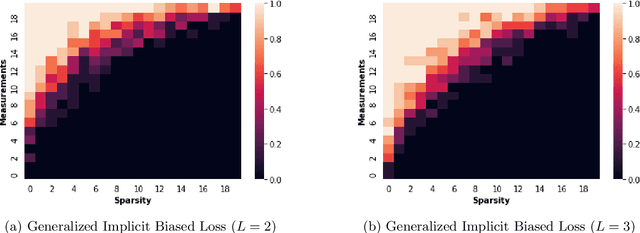
In deep learning it is common to overparameterize the neural networks, that is, to use more parameters than training samples. Quite surprisingly training the neural network via (stochastic) gradient descent leads to models that generalize very well, while classical statistics would suggest overfitting. In order to gain understanding of this implicit bias phenomenon we study the special case of sparse recovery (compressive sensing) which is of interest on its own. More precisely, in order to reconstruct a vector from underdetermined linear measurements, we introduce a corresponding overparameterized square loss functional, where the vector to be reconstructed is deeply factorized into several vectors. We show that, under a very mild assumption on the measurement matrix, vanilla gradient flow for the overparameterized loss functional converges to a solution of minimal $\ell_1$-norm. The latter is well-known to promote sparse solutions. As a by-product, our results significantly improve the sample complexity for compressive sensing in previous works. The theory accurately predicts the recovery rate in numerical experiments. For the proofs, we introduce the concept of {\textit{solution entropy}}, which bypasses the obstacles caused by non-convexity and should be of independent interest.

Gradient Descent for Deep Matrix Factorization: Dynamics and Implicit Bias towards Low Rank

We provide an explicit analysis of the dynamics of vanilla gradient descent for deep matrix factorization in a setting where the minimizer of the loss function is unique. We show that the recovery rate of ground-truth eigenvectors is proportional to the magnitude of the corresponding eigenvalues and that the differences among the rates are amplified as the depth of the factorization increases. For exactly characterized time intervals, the effective rank of gradient descent iterates is provably close to the effective rank of a low-rank projection of the ground-truth matrix, such that early stopping of gradient descent produces regularized solutions that may be used for denoising, for instance. In particular, apart from few initial steps of the iterations, the effective rank of our matrix is monotonically increasing, suggesting that "matrix factorization implicitly enforces gradient descent to take a route in which the effective rank is monotone". Since empirical observations in more general scenarios such as matrix sensing show a similar phenomenon, we believe that our theoretical results shed some light on the still mysterious "implicit bias" of gradient descent in deep learning.

Weighted Optimization: better generalization by smoother interpolation

We provide a rigorous analysis of how implicit bias towards smooth interpolations leads to low generalization error in the overparameterized setting. We provide the first case study of this connection through a random Fourier series model and weighted least squares. We then argue through this model and numerical experiments that normalization methods in deep learning such as weight normalization improve generalization in overparameterized neural networks by implicitly encouraging smooth interpolants.