AdaWAC: Adaptively Weighted Augmentation Consistency Regularization for Volumetric Medical Image Segmentation

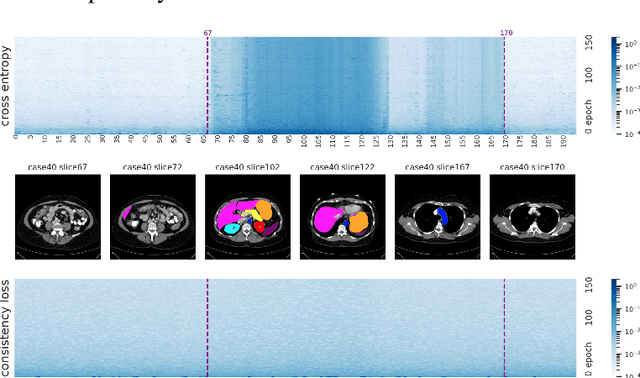
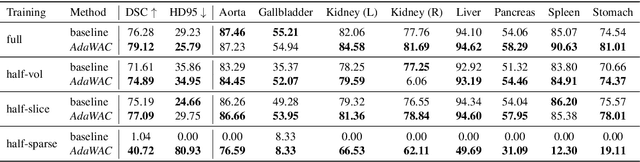
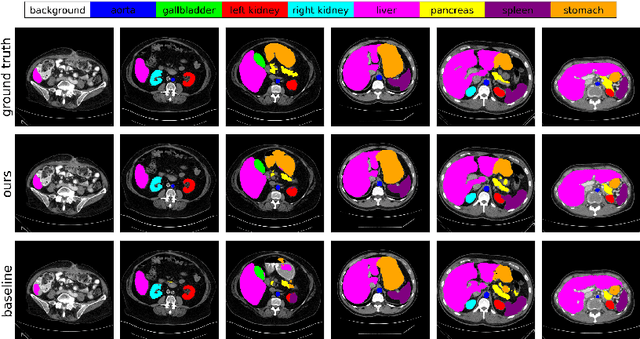
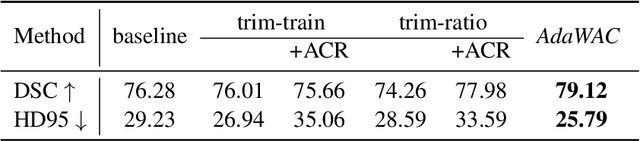
Sample reweighting is an effective strategy for learning from training data coming from a mixture of subpopulations. In volumetric medical image segmentation, the data inputs are similarly distributed, but the associated data labels fall into two subpopulations -- "label-sparse" and "label-dense" -- depending on whether the data image occurs near the beginning/end of the volumetric scan or the middle. Existing reweighting algorithms have focused on hard- and soft- thresholding of the label-sparse data, which results in loss of information and reduced sample efficiency by discarding valuable data input. For this setting, we propose AdaWAC as an adaptive weighting algorithm that introduces a set of trainable weights which, at the saddle point of the underlying objective, assigns label-dense samples to supervised cross-entropy loss and label-sparse samples to unsupervised consistency regularization. We provide a convergence guarantee for AdaWAC by recasting the optimization as online mirror descent on a saddle point problem. Moreover, we empirically demonstrate that AdaWAC not only enhances segmentation performance and sample efficiency but also improves robustness to the subpopulation shift in labels.

SHRIMP: Sparser Random Feature Models via Iterative Magnitude Pruning

Sparse shrunk additive models and sparse random feature models have been developed separately as methods to learn low-order functions, where there are few interactions between variables, but neither offers computational efficiency. On the other hand, $\ell_2$-based shrunk additive models are efficient but do not offer feature selection as the resulting coefficient vectors are dense. Inspired by the success of the iterative magnitude pruning technique in finding lottery tickets of neural networks, we propose a new method -- Sparser Random Feature Models via IMP (ShRIMP) -- to efficiently fit high-dimensional data with inherent low-dimensional structure in the form of sparse variable dependencies. Our method can be viewed as a combined process to construct and find sparse lottery tickets for two-layer dense networks. We explain the observed benefit of SHRIMP through a refined analysis on the generalization error for thresholded Basis Pursuit and resulting bounds on eigenvalues. From function approximation experiments on both synthetic data and real-world benchmark datasets, we show that SHRIMP obtains better than or competitive test accuracy compared to state-of-art sparse feature and additive methods such as SRFE-S, SSAM, and SALSA. Meanwhile, SHRIMP performs feature selection with low computational complexity and is robust to the pruning rate, indicating a robustness in the structure of the obtained subnetworks. We gain insight into the lottery ticket hypothesis through SHRIMP by noting a correspondence between our model and weight/neuron subnetworks.

AdaLoss: A computationally-efficient and provably convergent adaptive gradient method

We propose a computationally-friendly adaptive learning rate schedule, "AdaLoss", which directly uses the information of the loss function to adjust the stepsize in gradient descent methods. We prove that this schedule enjoys linear convergence in linear regression. Moreover, we provide a linear convergence guarantee over the non-convex regime, in the context of two-layer over-parameterized neural networks. If the width of the first-hidden layer in the two-layer networks is sufficiently large (polynomially), then AdaLoss converges robustly \emph{to the global minimum} in polynomial time. We numerically verify the theoretical results and extend the scope of the numerical experiments by considering applications in LSTM models for text clarification and policy gradients for control problems.

Weighted Optimization: better generalization by smoother interpolation

We provide a rigorous analysis of how implicit bias towards smooth interpolations leads to low generalization error in the overparameterized setting. We provide the first case study of this connection through a random Fourier series model and weighted least squares. We then argue through this model and numerical experiments that normalization methods in deep learning such as weight normalization improve generalization in overparameterized neural networks by implicitly encouraging smooth interpolants.

Linear Convergence of Adaptive Stochastic Gradient Descent

We prove that the norm version of the adaptive stochastic gradient method (AdaGrad-Norm) achieves a linear convergence rate for a subset of either strongly convex functions or non-convex functions that satisfy the Polyak-Lojasiewicz (PL) inequality. The paper introduces the notion of Restricted Uniform Inequality of Gradients (RUIG), which describes the uniform lower bound for the norm of the stochastic gradients with respect to the distance to the optimal solution. RUIG plays the key role in proving the robustness of AdaGrad-Norm to its hyper-parameter tuning. On top of RUIG, we develop a novel two-stage framework to prove linear convergence of AdaGrad-Norm without knowing the parameters of the objective functions: Stage I: the step-size decrease fast such that it reaches to Stage II; Stage II: the step-size decreases slowly and converges. This framework can likely be extended to other adaptive stepsize algorithms. The numerical experiments show desirable agreement with our theories.