PI-MFM: Physics-informed multimodal foundation model for solving partial differential equations

Partial differential equations (PDEs) govern a wide range of physical systems, and recent multimodal foundation models have shown promise for learning PDE solution operators across diverse equation families. However, existing multi-operator learning approaches are data-hungry and neglect physics during training. Here, we propose a physics-informed multimodal foundation model (PI-MFM) framework that directly enforces governing equations during pretraining and adaptation. PI-MFM takes symbolic representations of PDEs as the input, and automatically assembles PDE residual losses from the input expression via a vectorized derivative computation. These designs enable any PDE-encoding multimodal foundation model to be trained or adapted with unified physics-informed objectives across equation families. On a benchmark of 13 parametric one-dimensional time-dependent PDE families, PI-MFM consistently outperforms purely data-driven counterparts, especially with sparse labeled spatiotemporal points, partially observed time domains, or few labeled function pairs. Physics losses further improve robustness against noise, and simple strategies such as resampling collocation points substantially improve accuracy. We also analyze the accuracy, precision, and computational cost of automatic differentiation and finite differences for derivative computation within PI-MFM. Finally, we demonstrate zero-shot physics-informed fine-tuning to unseen PDE families: starting from a physics-informed pretrained model, adapting using only PDE residuals and initial/boundary conditions, without any labeled solution data, rapidly reduces test errors to around 1% and clearly outperforms physics-only training from scratch. These results show that PI-MFM provides a practical and scalable path toward data-efficient, transferable PDE solvers.

Regularized Random Fourier Features and Finite Element Reconstruction for Operator Learning in Sobolev Space

Operator learning is a data-driven approximation of mappings between infinite-dimensional function spaces, such as the solution operators of partial differential equations. Kernel-based operator learning can offer accurate, theoretically justified approximations that require less training than standard methods. However, they can become computationally prohibitive for large training sets and can be sensitive to noise. We propose a regularized random Fourier feature (RRFF) approach, coupled with a finite element reconstruction map (RRFF-FEM), for learning operators from noisy data. The method uses random features drawn from multivariate Student's $t$ distributions, together with frequency-weighted Tikhonov regularization that suppresses high-frequency noise. We establish high-probability bounds on the extreme singular values of the associated random feature matrix and show that when the number of features $N$ scales like $m \log m$ with the number of training samples $m$, the system is well-conditioned, which yields estimation and generalization guarantees. Detailed numerical experiments on benchmark PDE problems, including advection, Burgers', Darcy flow, Helmholtz, Navier-Stokes, and structural mechanics, demonstrate that RRFF and RRFF-FEM are robust to noise and achieve improved performance with reduced training time compared to the unregularized random feature model, while maintaining competitive accuracy relative to kernel and neural operator tests.

A Multimodal PDE Foundation Model for Prediction and Scientific Text Descriptions

Neural networks are one tool for approximating non-linear differential equations used in scientific computing tasks such as surrogate modeling, real-time predictions, and optimal control. PDE foundation models utilize neural networks to train approximations to multiple differential equations simultaneously and are thus a general purpose solver that can be adapted to downstream tasks. Current PDE foundation models focus on either learning general solution operators and/or the governing system of equations, and thus only handle numerical or symbolic modalities. However, real-world applications may require more flexible data modalities, e.g. text analysis or descriptive outputs. To address this gap, we propose a novel multimodal deep learning approach that leverages a transformer-based architecture to approximate solution operators for a wide variety of ODEs and PDEs. Our method integrates numerical inputs, such as equation parameters and initial conditions, with text descriptions of physical processes or system dynamics. This enables our model to handle settings where symbolic representations may be incomplete or unavailable. In addition to providing accurate numerical predictions, our approach generates interpretable scientific text descriptions, offering deeper insights into the underlying dynamics and solution properties. The numerical experiments show that our model provides accurate solutions for in-distribution data (with average relative error less than 3.3%) and out-of-distribution data (average relative error less than 7.8%) together with precise text descriptions (with correct descriptions generated 100% of times). In certain tests, the model is also shown to be capable of extrapolating solutions in time.

BCAT: A Block Causal Transformer for PDE Foundation Models for Fluid Dynamics

We introduce BCAT, a PDE foundation model designed for autoregressive prediction of solutions to two dimensional fluid dynamics problems. Our approach uses a block causal transformer architecture to model next frame predictions, leveraging previous frames as contextual priors rather than relying solely on sub-frames or pixel-based inputs commonly used in image generation methods. This block causal framework more effectively captures the spatial dependencies inherent in nonlinear spatiotemporal dynamics and physical phenomena. In an ablation study, next frame prediction demonstrated a 2.9x accuracy improvement over next token prediction. BCAT is trained on a diverse range of fluid dynamics datasets, including incompressible and compressible Navier-Stokes equations across various geometries and parameter regimes, as well as the shallow-water equations. The model's performance was evaluated on 6 distinct downstream prediction tasks and tested on about 8K trajectories to measure robustness on a variety of fluid dynamics simulations. BCAT achieved an average relative error of 1.92% across all evaluation tasks, outperforming prior approaches on standard benchmarks.

VICON: Vision In-Context Operator Networks for Multi-Physics Fluid Dynamics Prediction

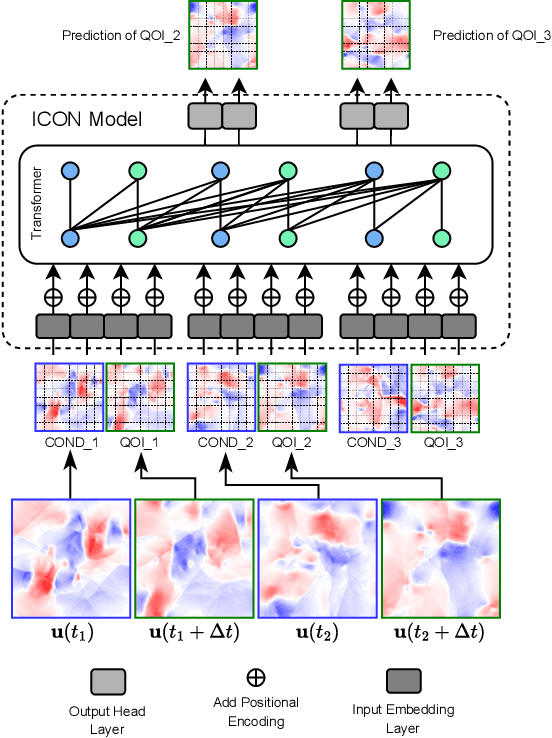
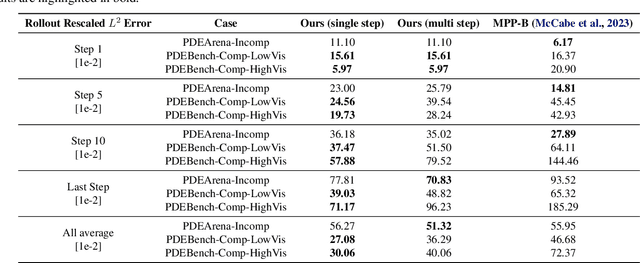
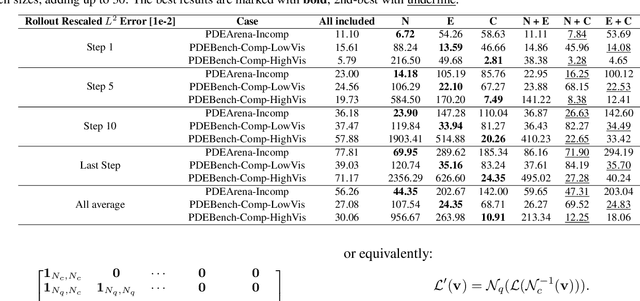
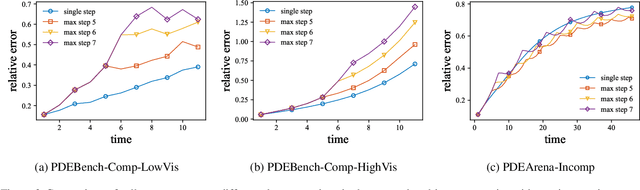
In-Context Operator Networks (ICONs) are models that learn operators across different types of PDEs using a few-shot, in-context approach. Although they show successful generalization to various PDEs, existing methods treat each data point as a single token, and suffer from computational inefficiency when processing dense data, limiting their application in higher spatial dimensions. In this work, we propose Vision In-Context Operator Networks (VICON), incorporating a vision transformer architecture that efficiently processes 2D functions through patch-wise operations. We evaluated our method on three fluid dynamics datasets, demonstrating both superior performance (reducing scaled $L^2$ error by $40\%$ and $61.6\%$ for two benchmark datasets for compressible flows, respectively) and computational efficiency (requiring only one-third of the inference time per frame) in long-term rollout predictions compared to the current state-of-the-art sequence-to-sequence model with fixed timestep prediction: Multiple Physics Pretraining (MPP). Compared to MPP, our method preserves the benefits of in-context operator learning, enabling flexible context formation when dealing with insufficient frame counts or varying timestep values.

DeepONet as a Multi-Operator Extrapolation Model: Distributed Pretraining with Physics-Informed Fine-Tuning

We propose a novel fine-tuning method to achieve multi-operator learning through training a distributed neural operator with diverse function data and then zero-shot fine-tuning the neural network using physics-informed losses for downstream tasks. Operator learning effectively approximates solution operators for PDEs and various PDE-related problems, yet it often struggles to generalize to new tasks. To address this, we investigate fine-tuning a pretrained model, while carefully selecting an initialization that enables rapid adaptation to new tasks with minimal data. Our approach combines distributed learning to integrate data from various operators in pre-training, while physics-informed methods enable zero-shot fine-tuning, minimizing the reliance on downstream data. We investigate standard fine-tuning and Low-Rank Adaptation fine-tuning, applying both to train complex nonlinear target operators that are difficult to learn only using random initialization. Through comprehensive numerical examples, we demonstrate the advantages of our approach, showcasing significant improvements in accuracy. Our findings provide a robust framework for advancing multi-operator learning and highlight the potential of transfer learning techniques in this domain.

Time-Series Forecasting, Knowledge Distillation, and Refinement within a Multimodal PDE Foundation Model

Symbolic encoding has been used in multi-operator learning as a way to embed additional information for distinct time-series data. For spatiotemporal systems described by time-dependent partial differential equations, the equation itself provides an additional modality to identify the system. The utilization of symbolic expressions along side time-series samples allows for the development of multimodal predictive neural networks. A key challenge with current approaches is that the symbolic information, i.e. the equations, must be manually preprocessed (simplified, rearranged, etc.) to match and relate to the existing token library, which increases costs and reduces flexibility, especially when dealing with new differential equations. We propose a new token library based on SymPy to encode differential equations as an additional modality for time-series models. The proposed approach incurs minimal cost, is automated, and maintains high prediction accuracy for forecasting tasks. Additionally, we include a Bayesian filtering module that connects the different modalities to refine the learned equation. This improves the accuracy of the learned symbolic representation and the predicted time-series.

PROSE-FD: A Multimodal PDE Foundation Model for Learning Multiple Operators for Forecasting Fluid Dynamics

We propose PROSE-FD, a zero-shot multimodal PDE foundational model for simultaneous prediction of heterogeneous two-dimensional physical systems related to distinct fluid dynamics settings. These systems include shallow water equations and the Navier-Stokes equations with incompressible and compressible flow, regular and complex geometries, and different buoyancy settings. This work presents a new transformer-based multi-operator learning approach that fuses symbolic information to perform operator-based data prediction, i.e. non-autoregressive. By incorporating multiple modalities in the inputs, the PDE foundation model builds in a pathway for including mathematical descriptions of the physical behavior. We pre-train our foundation model on 6 parametric families of equations collected from 13 datasets, including over 60K trajectories. Our model outperforms popular operator learning, computer vision, and multi-physics models, in benchmark forward prediction tasks. We test our architecture choices with ablation studies.

LeMON: Learning to Learn Multi-Operator Networks

Single-operator learning involves training a deep neural network to learn a specific operator, whereas recent work in multi-operator learning uses an operator embedding structure to train a single neural network on data from multiple operators. Thus, multi-operator learning is capable of predicting a range of operators within one model. In this work, we propose pretraining and fine-tuning strategies for solving PDEs using multi-operator learning. One key aspect is that by increasing the number of families of operators used in pretraining, a PDE foundation model can be fine-tuned to downstream tasks involving new PDEs with a limited number of samples, thus outperforming single operator neural networks. Specifically, a multi-operator learning model pre-trained with data from diverse PDE families can predict unseen operators after fine-tuning with only a limited number of operators from the new family, enabling them to serve as a data-free PDE solver. We also show that the proposed training and fine-tuning method is able to predict new operators in zero-shot prediction without samples. Additionally, we introduce a PDE-agnostic meta-learning algorithm to improve the adaptability of the model to various PDEs by providing a better parameter initialization process. To address the needs of applications with limited computing resources, we explore low-rank adaptation methods that reduce computational costs while enhancing solver accuracy. Lastly, by examining the scaling law with respect to the number of operator families, we establish and highlight its potential for broad adaptation in PDE-solving tasks.

Towards a Foundation Model for Partial Differential Equations: Multi-Operator Learning and Extrapolation

Foundation models, such as large language models, have demonstrated success in addressing various language and image processing tasks. In this work, we introduce a multi-modal foundation model for scientific problems, named PROSE-PDE. Our model, designed for bi-modality to bi-modality learning, is a multi-operator learning approach which can predict future states of spatiotemporal systems while concurrently learning the underlying governing equations of the physical system. Specifically, we focus on multi-operator learning by training distinct one-dimensional time-dependent nonlinear constant coefficient partial differential equations, with potential applications to many physical applications including physics, geology, and biology. More importantly, we provide three extrapolation studies to demonstrate that PROSE-PDE can generalize physical features through the robust training of multiple operators and that the proposed model can extrapolate to predict PDE solutions whose models or data were unseen during the training. Furthermore, we show through systematic numerical experiments that the utilization of the symbolic modality in our model effectively resolves the well-posedness problems with training multiple operators and thus enhances our model's predictive capabilities.