Neural Networks for Threshold Dynamics Reconstruction

We introduce two convolutional neural network (CNN) architectures, inspired by the Merriman-Bence-Osher (MBO) algorithm and by cellular automatons, to model and learn threshold dynamics for front evolution from video data. The first model, termed the (single-dynamics) MBO network, learns a specific kernel and threshold for each input video without adapting to new dynamics, while the second, a meta-learning MBO network, generalizes across diverse threshold dynamics by adapting its parameters per input. Both models are evaluated on synthetic and real-world videos (ice melting and fire front propagation), with performance metrics indicating effective reconstruction and extrapolation of evolving boundaries, even under noisy conditions. Empirical results highlight the robustness of both networks across varied synthetic and real-world dynamics.

LoDIP: Low light phase retrieval with deep image prior

Phase retrieval (PR) is a fundamental challenge in scientific imaging, enabling nanoscale techniques like coherent diffractive imaging (CDI). Imaging at low radiation doses becomes important in applications where samples are susceptible to radiation damage. However, most PR methods struggle in low dose scenario due to the presence of very high shot noise. Advancements in the optical data acquisition setup, exemplified by in-situ CDI, have shown potential for low-dose imaging. But these depend on a time series of measurements, rendering them unsuitable for single-image applications. Similarly, on the computational front, data-driven phase retrieval techniques are not readily adaptable to the single-image context. Deep learning based single-image methods, such as deep image prior, have been effective for various imaging tasks but have exhibited limited success when applied to PR. In this work, we propose LoDIP which combines the in-situ CDI setup with the power of implicit neural priors to tackle the problem of single-image low-dose phase retrieval. Quantitative evaluations demonstrate the superior performance of LoDIP on this task as well as applicability to real experimental scenarios.

Applications of ML-Based Surrogates in Bayesian Approaches to Inverse Problems

Neural networks have become a powerful tool as surrogate models to provide numerical solutions for scientific problems with increased computational efficiency. This efficiency can be advantageous for numerically challenging problems where time to solution is important or when evaluation of many similar analysis scenarios is required. One particular area of scientific interest is the setting of inverse problems, where one knows the forward dynamics of a system are described by a partial differential equation and the task is to infer properties of the system given (potentially noisy) observations of these dynamics. We consider the inverse problem of inferring the location of a wave source on a square domain, given a noisy solution to the 2-D acoustic wave equation. Under the assumption of Gaussian noise, a likelihood function for source location can be formulated, which requires one forward simulation of the system per evaluation. Using a standard neural network as a surrogate model makes it computationally feasible to evaluate this likelihood several times, and so Markov Chain Monte Carlo methods can be used to evaluate the posterior distribution of the source location. We demonstrate that this method can accurately infer source-locations from noisy data.

Applications of No-Collision Transportation Maps in Manifold Learning

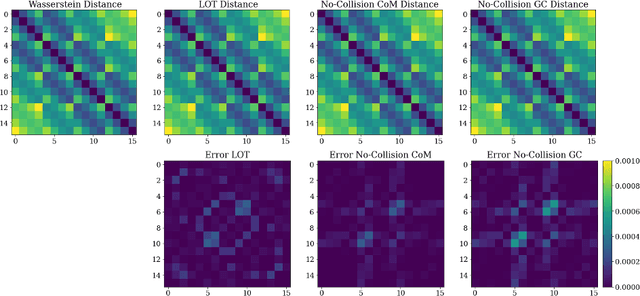
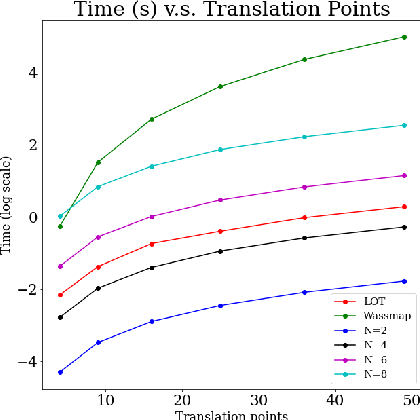
In this work, we investigate applications of no-collision transportation maps introduced in [Nurbekyan et. al., 2020] in manifold learning for image data. Recently, there has been a surge in applying transportation-based distances and features for data representing motion-like or deformation-like phenomena. Indeed, comparing intensities at fixed locations often does not reveal the data structure. No-collision maps and distances developed in [Nurbekyan et. al., 2020] are sensitive to geometric features similar to optimal transportation (OT) maps but much cheaper to compute due to the absence of optimization. In this work, we prove that no-collision distances provide an isometry between translations (respectively dilations) of a single probability measure and the translation (respectively dilation) vectors equipped with a Euclidean distance. Furthermore, we prove that no-collision transportation maps, as well as OT and linearized OT maps, do not in general provide an isometry for rotations. The numerical experiments confirm our theoretical findings and show that no-collision distances achieve similar or better performance on several manifold learning tasks compared to other OT and Euclidean-based methods at a fraction of a computational cost.

A Neural Network Ensemble Approach to System Identification

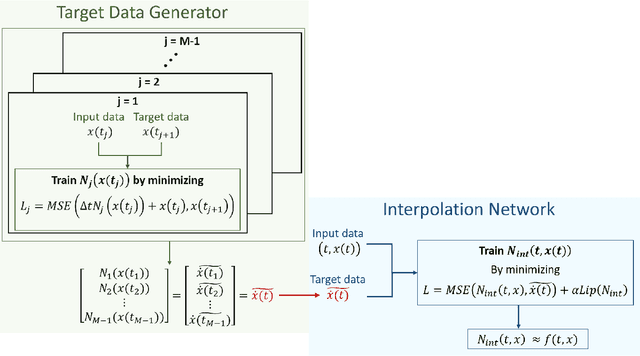
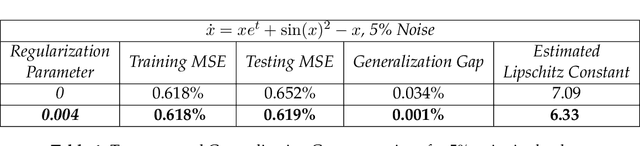
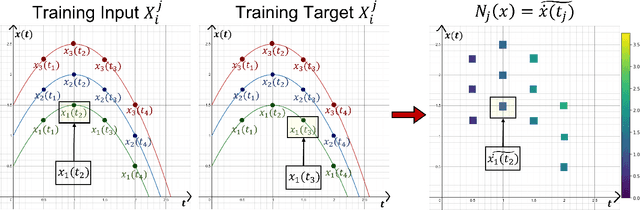
We present a new algorithm for learning unknown governing equations from trajectory data, using and ensemble of neural networks. Given samples of solutions $x(t)$ to an unknown dynamical system $\dot{x}(t)=f(t,x(t))$, we approximate the function $f$ using an ensemble of neural networks. We express the equation in integral form and use Euler method to predict the solution at every successive time step using at each iteration a different neural network as a prior for $f$. This procedure yields M-1 time-independent networks, where M is the number of time steps at which $x(t)$ is observed. Finally, we obtain a single function $f(t,x(t))$ by neural network interpolation. Unlike our earlier work, where we numerically computed the derivatives of data, and used them as target in a Lipschitz regularized neural network to approximate $f$, our new method avoids numerical differentiations, which are unstable in presence of noise. We test the new algorithm on multiple examples both with and without noise in the data. We empirically show that generalization and recovery of the governing equation improve by adding a Lipschitz regularization term in our loss function and that this method improves our previous one especially in presence of noise, when numerical differentiation provides low quality target data. Finally, we compare our results with the method proposed by Raissi, et al. arXiv:1801.01236 (2018) and with SINDy.

System Identification Through Lipschitz Regularized Deep Neural Networks

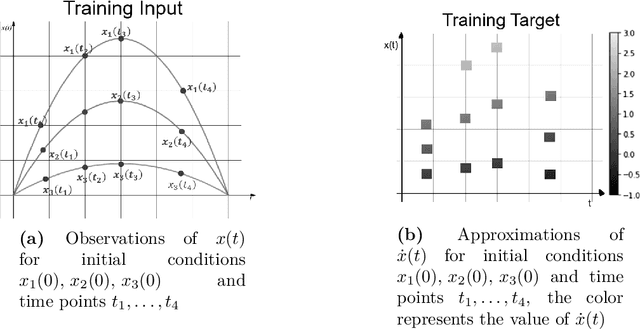
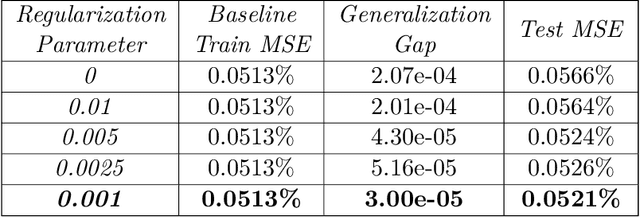
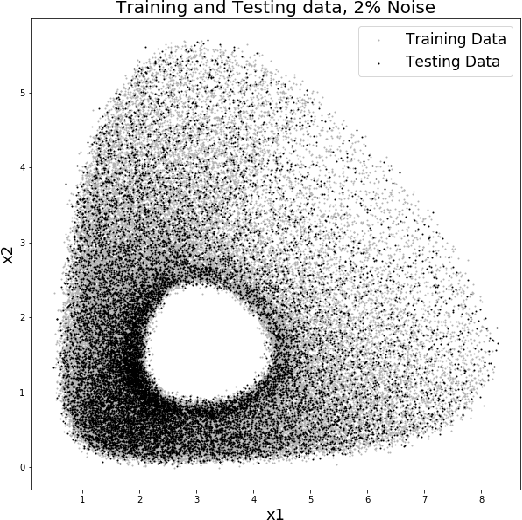
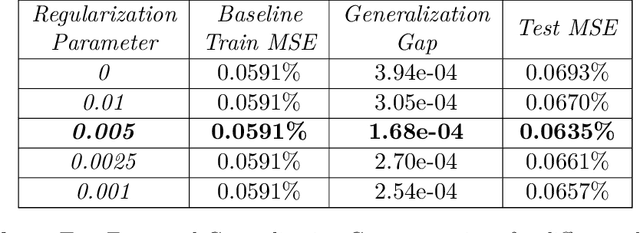
In this paper we use neural networks to learn governing equations from data. Specifically we reconstruct the right-hand side of a system of ODEs $\dot{x}(t) = f(t, x(t))$ directly from observed uniformly time-sampled data using a neural network. In contrast with other neural network based approaches to this problem, we add a Lipschitz regularization term to our loss function. In the synthetic examples we observed empirically that this regularization results in a smoother approximating function and better generalization properties when compared with non-regularized models, both on trajectory and non-trajectory data, especially in presence of noise. In contrast with sparse regression approaches, since neural networks are universal approximators, we don't need any prior knowledge on the ODE system. Since the model is applied component wise, it can handle systems of any dimension, making it usable for real-world data.