Neural Networks for Threshold Dynamics Reconstruction

We introduce two convolutional neural network (CNN) architectures, inspired by the Merriman-Bence-Osher (MBO) algorithm and by cellular automatons, to model and learn threshold dynamics for front evolution from video data. The first model, termed the (single-dynamics) MBO network, learns a specific kernel and threshold for each input video without adapting to new dynamics, while the second, a meta-learning MBO network, generalizes across diverse threshold dynamics by adapting its parameters per input. Both models are evaluated on synthetic and real-world videos (ice melting and fire front propagation), with performance metrics indicating effective reconstruction and extrapolation of evolving boundaries, even under noisy conditions. Empirical results highlight the robustness of both networks across varied synthetic and real-world dynamics.

A Neural Network Ensemble Approach to System Identification

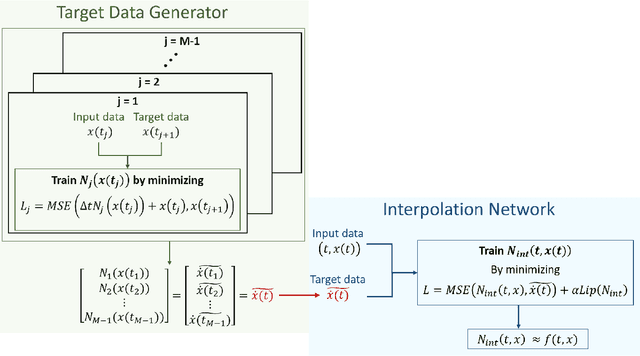
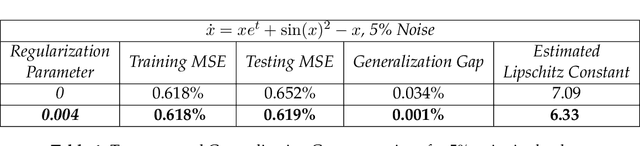
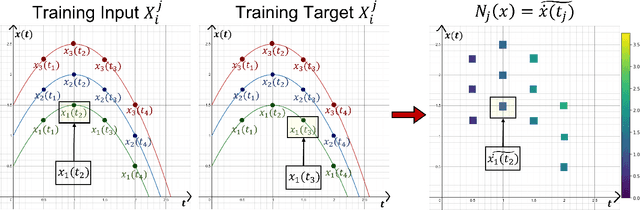
We present a new algorithm for learning unknown governing equations from trajectory data, using and ensemble of neural networks. Given samples of solutions $x(t)$ to an unknown dynamical system $\dot{x}(t)=f(t,x(t))$, we approximate the function $f$ using an ensemble of neural networks. We express the equation in integral form and use Euler method to predict the solution at every successive time step using at each iteration a different neural network as a prior for $f$. This procedure yields M-1 time-independent networks, where M is the number of time steps at which $x(t)$ is observed. Finally, we obtain a single function $f(t,x(t))$ by neural network interpolation. Unlike our earlier work, where we numerically computed the derivatives of data, and used them as target in a Lipschitz regularized neural network to approximate $f$, our new method avoids numerical differentiations, which are unstable in presence of noise. We test the new algorithm on multiple examples both with and without noise in the data. We empirically show that generalization and recovery of the governing equation improve by adding a Lipschitz regularization term in our loss function and that this method improves our previous one especially in presence of noise, when numerical differentiation provides low quality target data. Finally, we compare our results with the method proposed by Raissi, et al. arXiv:1801.01236 (2018) and with SINDy.

System Identification Through Lipschitz Regularized Deep Neural Networks

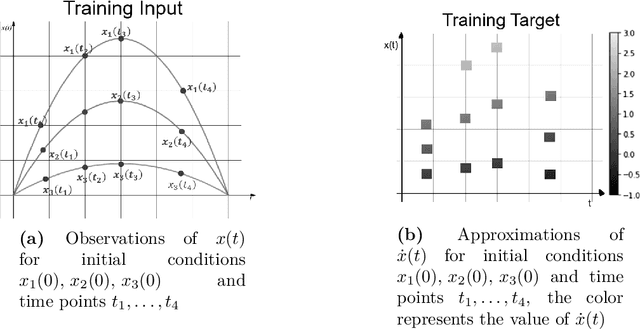
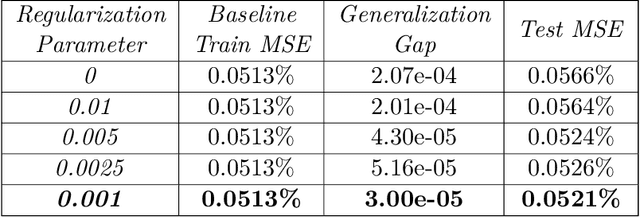
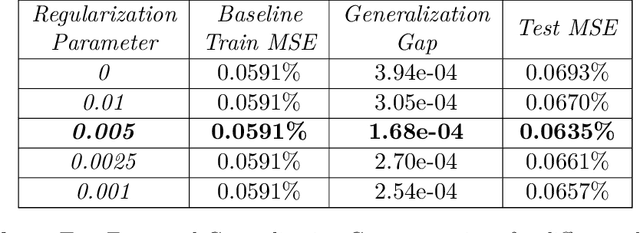
In this paper we use neural networks to learn governing equations from data. Specifically we reconstruct the right-hand side of a system of ODEs $\dot{x}(t) = f(t, x(t))$ directly from observed uniformly time-sampled data using a neural network. In contrast with other neural network based approaches to this problem, we add a Lipschitz regularization term to our loss function. In the synthetic examples we observed empirically that this regularization results in a smoother approximating function and better generalization properties when compared with non-regularized models, both on trajectory and non-trajectory data, especially in presence of noise. In contrast with sparse regression approaches, since neural networks are universal approximators, we don't need any prior knowledge on the ODE system. Since the model is applied component wise, it can handle systems of any dimension, making it usable for real-world data.