Paramjyoti Mohapatra
Applications of ML-Based Surrogates in Bayesian Approaches to Inverse Problems
Oct 23, 2023


Abstract:Neural networks have become a powerful tool as surrogate models to provide numerical solutions for scientific problems with increased computational efficiency. This efficiency can be advantageous for numerically challenging problems where time to solution is important or when evaluation of many similar analysis scenarios is required. One particular area of scientific interest is the setting of inverse problems, where one knows the forward dynamics of a system are described by a partial differential equation and the task is to infer properties of the system given (potentially noisy) observations of these dynamics. We consider the inverse problem of inferring the location of a wave source on a square domain, given a noisy solution to the 2-D acoustic wave equation. Under the assumption of Gaussian noise, a likelihood function for source location can be formulated, which requires one forward simulation of the system per evaluation. Using a standard neural network as a surrogate model makes it computationally feasible to evaluate this likelihood several times, and so Markov Chain Monte Carlo methods can be used to evaluate the posterior distribution of the source location. We demonstrate that this method can accurately infer source-locations from noisy data.
A Geometric Flow Approach for Segmentation of Images with Inhomongeneous Intensity and Missing Boundaries
Sep 19, 2023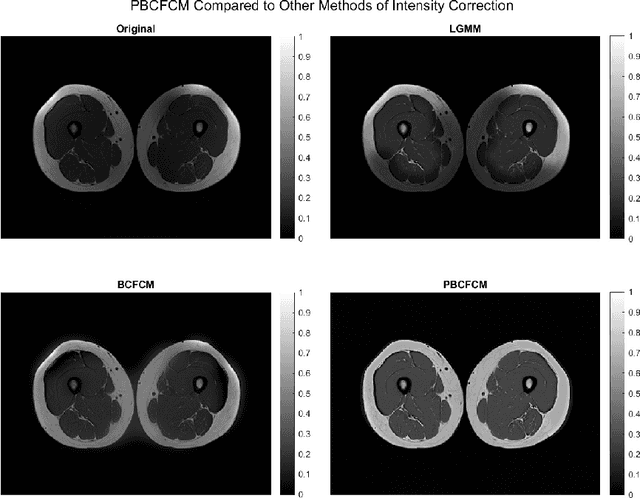
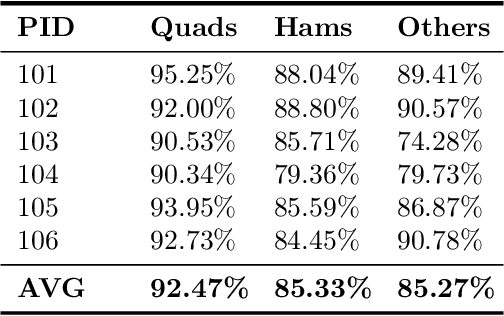
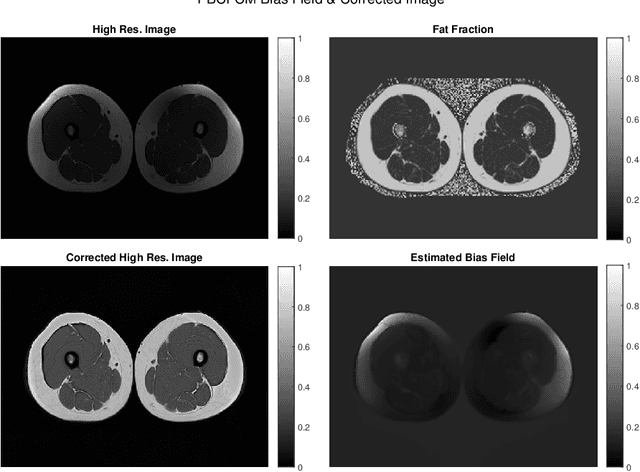

Abstract:Image segmentation is a complex mathematical problem, especially for images that contain intensity inhomogeneity and tightly packed objects with missing boundaries in between. For instance, Magnetic Resonance (MR) muscle images often contain both of these issues, making muscle segmentation especially difficult. In this paper we propose a novel intensity correction and a semi-automatic active contour based segmentation approach. The approach uses a geometric flow that incorporates a reproducing kernel Hilbert space (RKHS) edge detector and a geodesic distance penalty term from a set of markers and anti-markers. We test the proposed scheme on MR muscle segmentation and compare with some state of the art methods. To help deal with the intensity inhomogeneity in this particular kind of image, a new approach to estimate the bias field using a fat fraction image, called Prior Bias-Corrected Fuzzy C-means (PBCFCM), is introduced. Numerical experiments show that the proposed scheme leads to significantly better results than compared ones. The average dice values of the proposed method are 92.5%, 85.3%, 85.3% for quadriceps, hamstrings and other muscle groups while other approaches are at least 10% worse.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge