Detection-Guided Deep Learning-Based Model with Spatial Regularization for Lung Nodule Segmentation

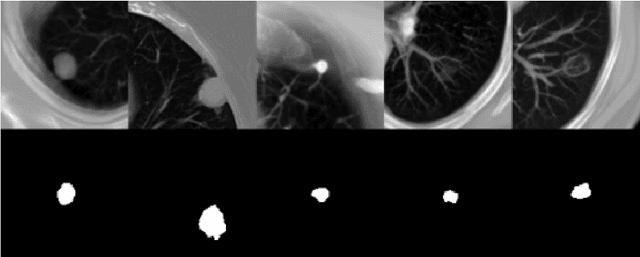
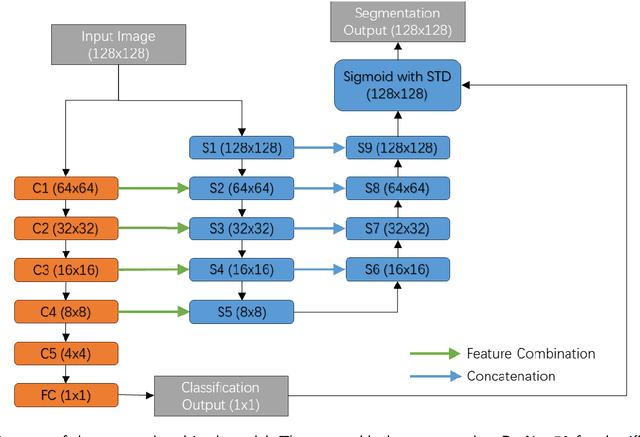
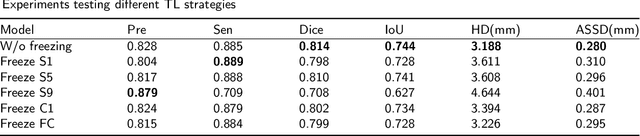
Lung cancer ranks as one of the leading causes of cancer diagnosis and is the foremost cause of cancer-related mortality worldwide. The early detection of lung nodules plays a pivotal role in improving outcomes for patients, as it enables timely and effective treatment interventions. The segmentation of lung nodules plays a critical role in aiding physicians in distinguishing between malignant and benign lesions. However, this task remains challenging due to the substantial variation in the shapes and sizes of lung nodules, and their frequent proximity to lung tissues, which complicates clear delineation. In this study, we introduce a novel model for segmenting lung nodules in computed tomography (CT) images, leveraging a deep learning framework that integrates segmentation and classification processes. This model is distinguished by its use of feature combination blocks, which facilitate the sharing of information between the segmentation and classification components. Additionally, we employ the classification outcomes as priors to refine the size estimation of the predicted nodules, integrating these with a spatial regularization technique to enhance precision. Furthermore, recognizing the challenges posed by limited training datasets, we have developed an optimal transfer learning strategy that freezes certain layers to further improve performance. The results show that our proposed model can capture the target nodules more accurately compared to other commonly used models. By applying transfer learning, the performance can be further improved, achieving a sensitivity score of 0.885 and a Dice score of 0.814.

Time-Varying Graph Signal Recovery Using High-Order Smoothness and Adaptive Low-rankness

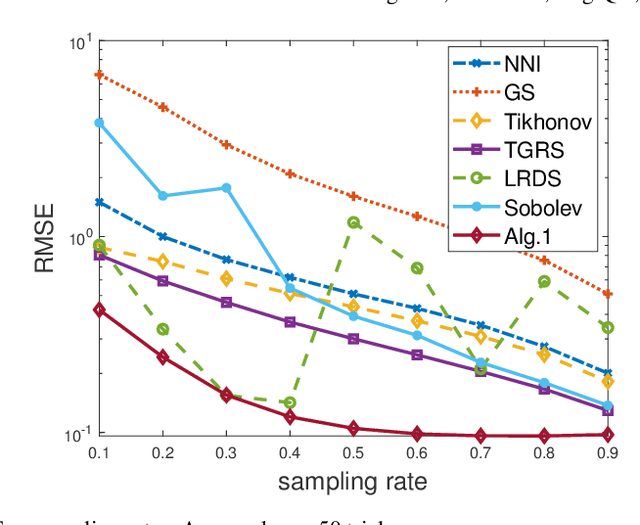
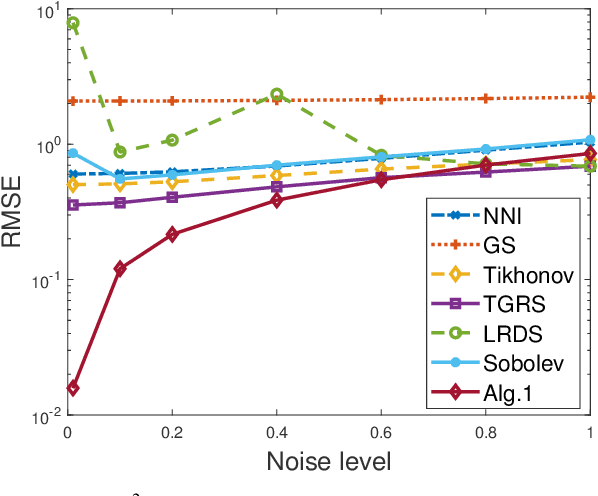
Time-varying graph signal recovery has been widely used in many applications, including climate change, environmental hazard monitoring, and epidemic studies. It is crucial to choose appropriate regularizations to describe the characteristics of the underlying signals, such as the smoothness of the signal over the graph domain and the low-rank structure of the spatial-temporal signal modeled in a matrix form. As one of the most popular options, the graph Laplacian is commonly adopted in designing graph regularizations for reconstructing signals defined on a graph from partially observed data. In this work, we propose a time-varying graph signal recovery method based on the high-order Sobolev smoothness and an error-function weighted nuclear norm regularization to enforce the low-rankness. Two efficient algorithms based on the alternating direction method of multipliers and iterative reweighting are proposed, and convergence of one algorithm is shown in detail. We conduct various numerical experiments on synthetic and real-world data sets to demonstrate the proposed method's effectiveness compared to the state-of-the-art in graph signal recovery.

A Geometric Flow Approach for Segmentation of Images with Inhomongeneous Intensity and Missing Boundaries

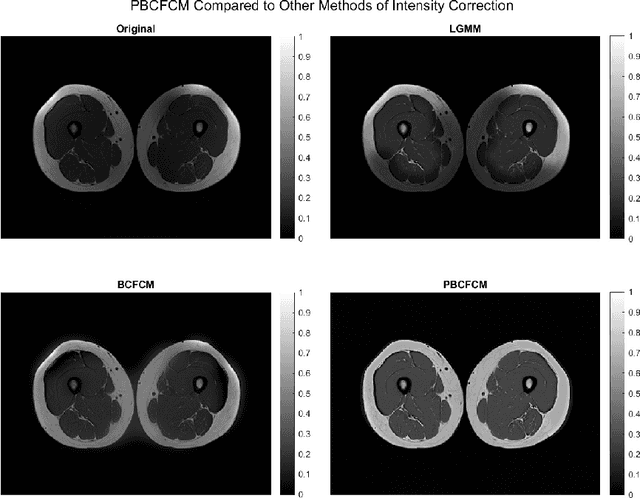
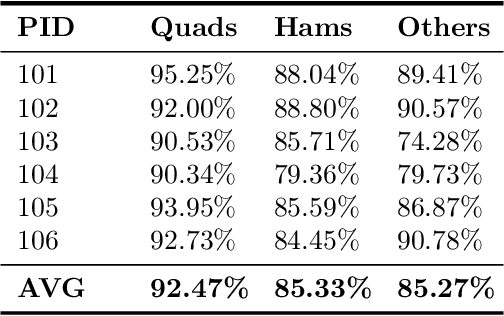
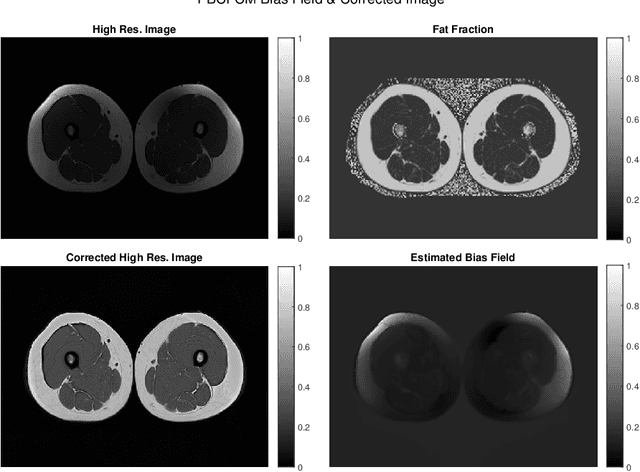
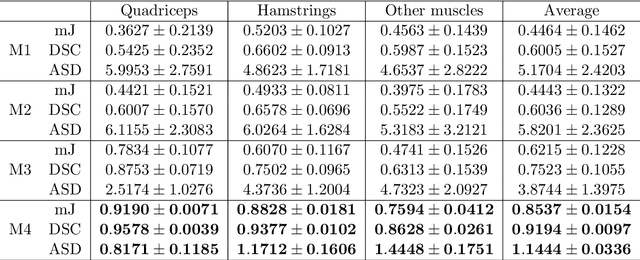
Image segmentation is a complex mathematical problem, especially for images that contain intensity inhomogeneity and tightly packed objects with missing boundaries in between. For instance, Magnetic Resonance (MR) muscle images often contain both of these issues, making muscle segmentation especially difficult. In this paper we propose a novel intensity correction and a semi-automatic active contour based segmentation approach. The approach uses a geometric flow that incorporates a reproducing kernel Hilbert space (RKHS) edge detector and a geodesic distance penalty term from a set of markers and anti-markers. We test the proposed scheme on MR muscle segmentation and compare with some state of the art methods. To help deal with the intensity inhomogeneity in this particular kind of image, a new approach to estimate the bias field using a fat fraction image, called Prior Bias-Corrected Fuzzy C-means (PBCFCM), is introduced. Numerical experiments show that the proposed scheme leads to significantly better results than compared ones. The average dice values of the proposed method are 92.5%, 85.3%, 85.3% for quadriceps, hamstrings and other muscle groups while other approaches are at least 10% worse.

Interpretable Small Training Set Image Segmentation Network Originated from Multi-Grid Variational Model

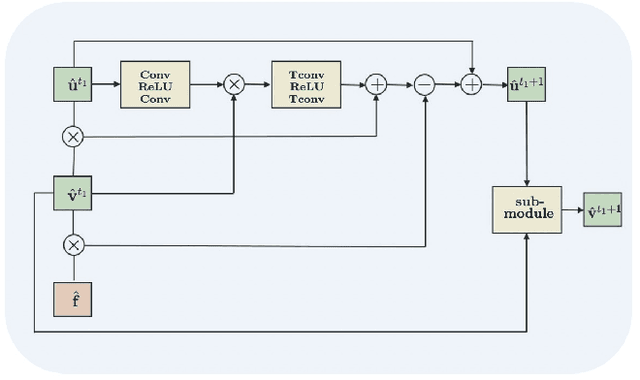
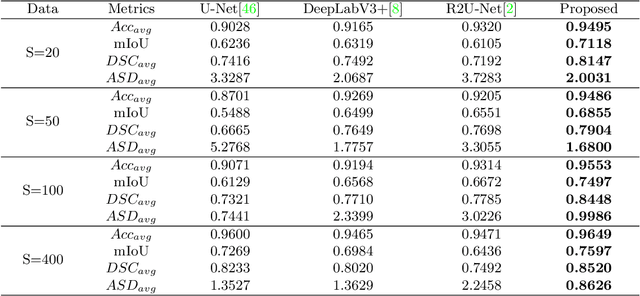
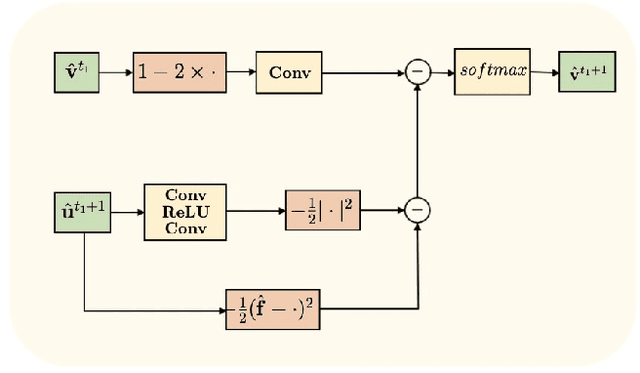
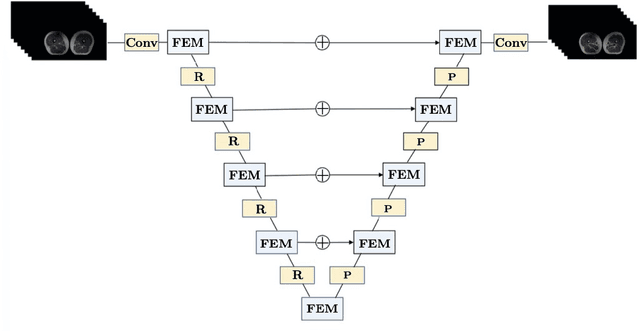
The main objective of image segmentation is to divide an image into homogeneous regions for further analysis. This is a significant and crucial task in many applications such as medical imaging. Deep learning (DL) methods have been proposed and widely used for image segmentation. However, these methods usually require a large amount of manually segmented data as training data and suffer from poor interpretability (known as the black box problem). The classical Mumford-Shah (MS) model is effective for segmentation and provides a piece-wise smooth approximation of the original image. In this paper, we replace the hand-crafted regularity term in the MS model with a data adaptive generalized learnable regularity term and use a multi-grid framework to unroll the MS model and obtain a variational model-based segmentation network with better generalizability and interpretability. This approach allows for the incorporation of learnable prior information into the network structure design. Moreover, the multi-grid framework enables multi-scale feature extraction and offers a mathematical explanation for the effectiveness of the U-shaped network structure in producing good image segmentation results. Due to the proposed network originates from a variational model, it can also handle small training sizes. Our experiments on the REFUGE dataset, the White Blood Cell image dataset, and 3D thigh muscle magnetic resonance (MR) images demonstrate that even with smaller training datasets, our method yields better segmentation results compared to related state of the art segmentation methods.

Image Segmentation with Adaptive Spatial Priors from Joint Registration

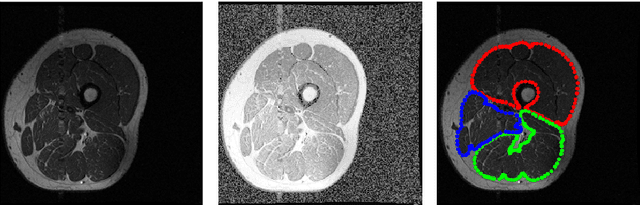
Image segmentation is a crucial but challenging task that has many applications. In medical imaging for instance, intensity inhomogeneity and noise are common. In thigh muscle images, different muscles are closed packed together and there are often no clear boundaries between them. Intensity based segmentation models cannot separate one muscle from another. To solve such problems, in this work we present a segmentation model with adaptive spatial priors from joint registration. This model combines segmentation and registration in a unified framework to leverage their positive mutual influence. The segmentation is based on a modified Gaussian mixture model (GMM), which integrates intensity inhomogeneity and spacial smoothness. The registration plays the role of providing a shape prior. We adopt a modified sum of squared difference (SSD) fidelity term and Tikhonov regularity term for registration, and also utilize Gaussian pyramid and parametric method for robustness. The connection between segmentation and registration is guaranteed by the cross entropy metric that aims to make the segmentation map (from segmentation) and deformed atlas (from registration) as similar as possible. This joint framework is implemented within a constraint optimization framework, which leads to an efficient algorithm. We evaluate our proposed model on synthetic and thigh muscle MR images. Numerical results show the improvement as compared to segmentation and registration performed separately and other joint models.

PCM-TV-TFV: A Novel Two Stage Framework for Image Reconstruction from Fourier Data

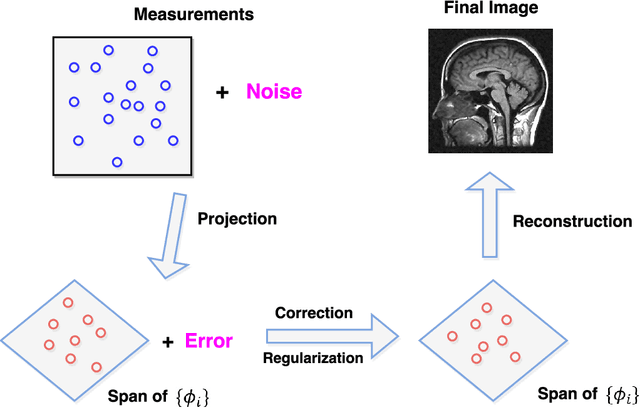
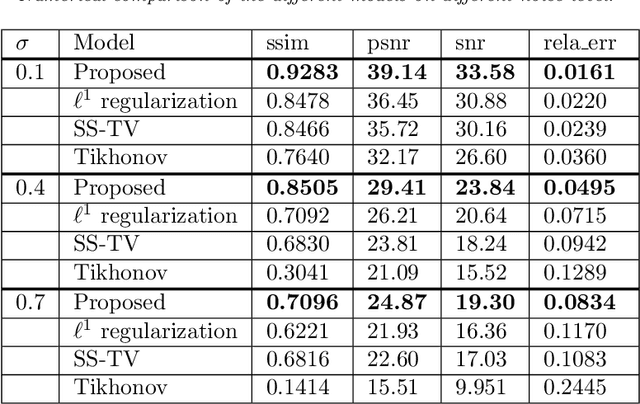
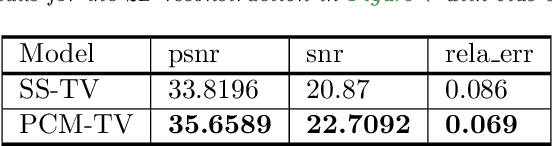
We propose in this paper a novel two-stage Projection Correction Modeling (PCM) framework for image reconstruction from (non-uniform) Fourier measurements. PCM consists of a projection stage (P-stage) motivated by the multi-scale Galerkin method and a correction stage (C-stage) with an edge guided regularity fusing together the advantages of total variation (TV) and total fractional variation (TFV). The P-stage allows for continuous modeling of the underlying image of interest. The given measurements are projected onto a space in which the image is well represented. We then enhance the reconstruction result at the C-stage that minimizes an energy functional consisting of a fidelity in the transformed domain and a novel edge guided regularity. We further develop efficient proximal algorithms to solve the corresponding optimization problem. Various numerical results in both 1D signals and 2D images have also been presented to demonstrate the superior performance of the proposed two-stage method to other classical one-stage methods.

Single image super-resolution by approximated Heaviside functions

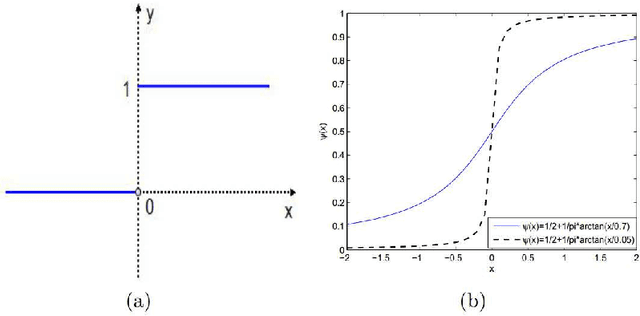
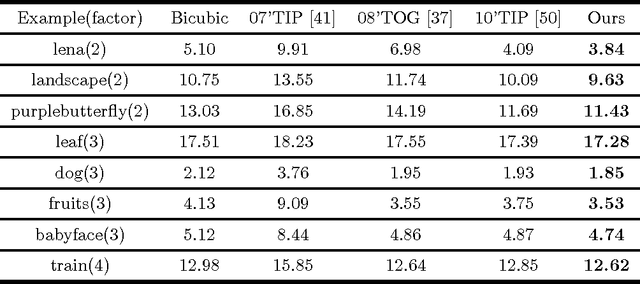
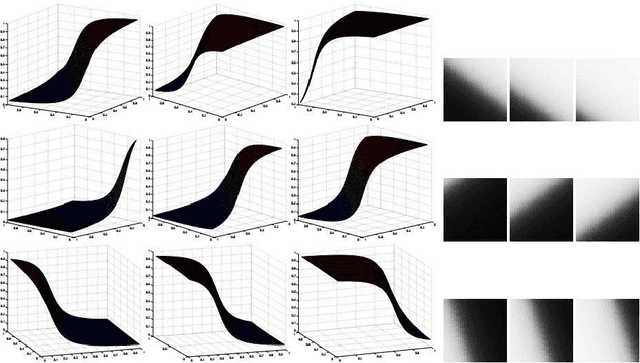
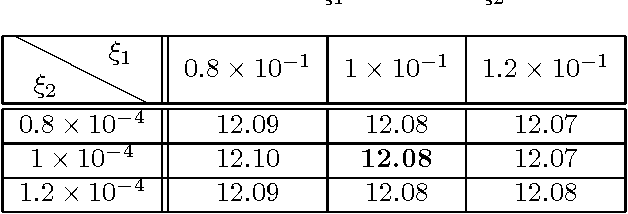
Image super-resolution is a process to enhance image resolution. It is widely used in medical imaging, satellite imaging, target recognition, etc. In this paper, we conduct continuous modeling and assume that the unknown image intensity function is defined on a continuous domain and belongs to a space with a redundant basis. We propose a new iterative model for single image super-resolution based on an observation: an image is consisted of smooth components and non-smooth components, and we use two classes of approximated Heaviside functions (AHFs) to represent them respectively. Due to sparsity of the non-smooth components, a $L_{1}$ model is employed. In addition, we apply the proposed iterative model to image patches to reduce computation and storage. Comparisons with some existing competitive methods show the effectiveness of the proposed method.

Two-stage Geometric Information Guided Image Reconstruction

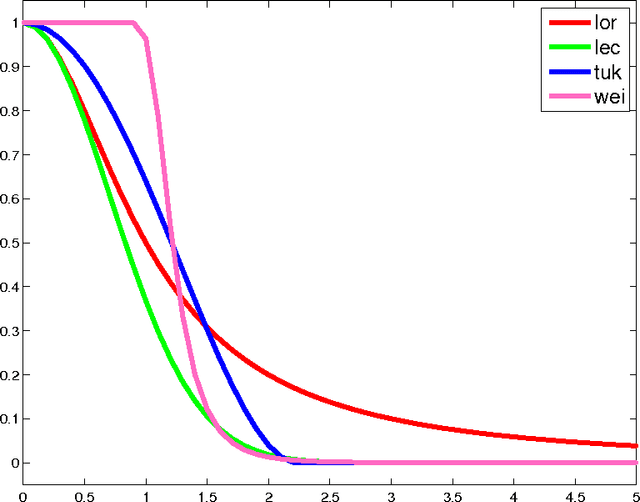
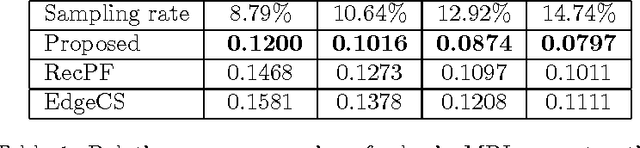
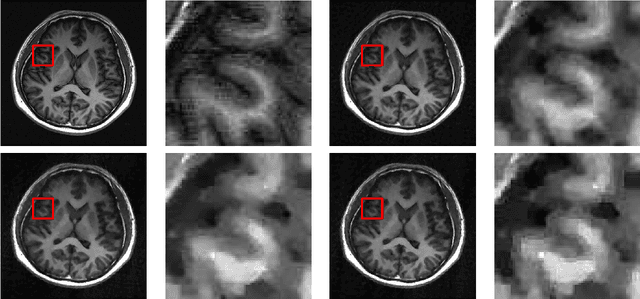
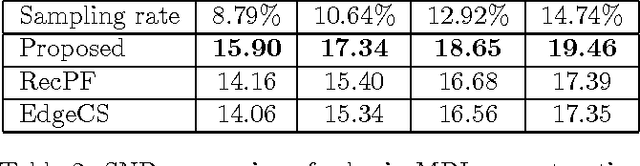
In compressive sensing, it is challenging to reconstruct image of high quality from very few noisy linear projections. Existing methods mostly work well on piecewise constant images but not so well on piecewise smooth images such as natural images, medical images that contain a lot of details. We propose a two-stage method called GeoCS to recover images with rich geometric information from very limited amount of noisy measurements. The method adopts the shearlet transform that is mathematically proven to be optimal in sparsely representing images containing anisotropic features such as edges, corners, spikes etc. It also uses the weighted total variation (TV) sparsity with spatially variant weights to preserve sharp edges but to reduce the staircase effects of TV. Geometric information extracted from the results of stage I serves as an initial prior for stage II which alternates image reconstruction and geometric information update in a mutually beneficial way. GeoCS has been tested on incomplete spectral Fourier samples. It is applicable to other types of measurements as well. Experimental results on various complicated images show that GeoCS is efficient and generates high-quality images.