Guohui Song
Hyperparameter Estimation for Sparse Bayesian Learning Models
Jan 04, 2024Abstract:Sparse Bayesian Learning (SBL) models are extensively used in signal processing and machine learning for promoting sparsity through hierarchical priors. The hyperparameters in SBL models are crucial for the model's performance, but they are often difficult to estimate due to the non-convexity and the high-dimensionality of the associated objective function. This paper presents a comprehensive framework for hyperparameter estimation in SBL models, encompassing well-known algorithms such as the expectation-maximization (EM), MacKay, and convex bounding (CB) algorithms. These algorithms are cohesively interpreted within an alternating minimization and linearization (AML) paradigm, distinguished by their unique linearized surrogate functions. Additionally, a novel algorithm within the AML framework is introduced, showing enhanced efficiency, especially under low signal noise ratios. This is further improved by a new alternating minimization and quadratic approximation (AMQ) paradigm, which includes a proximal regularization term. The paper substantiates these advancements with thorough convergence analysis and numerical experiments, demonstrating the algorithm's effectiveness in various noise conditions and signal-to-noise ratios.
Sequential edge detection using joint hierarchical Bayesian learning
Feb 28, 2023Abstract:This paper introduces a new sparse Bayesian learning (SBL) algorithm that jointly recovers a temporal sequence of edge maps from noisy and under-sampled Fourier data. The new method is cast in a Bayesian framework and uses a prior that simultaneously incorporates intra-image information to promote sparsity in each individual edge map with inter-image information to promote similarities in any unchanged regions. By treating both the edges as well as the similarity between adjacent images as random variables, there is no need to separately form regions of change. Thus we avoid both additional computational cost as well as any information loss resulting from pre-processing the image. Our numerical examples demonstrate that our new method compares favorably with more standard SBL approaches.
A Divide-and-Conquer Algorithm for Distributed Optimization on Networks
Dec 03, 2021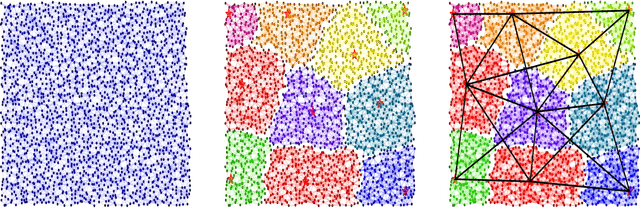
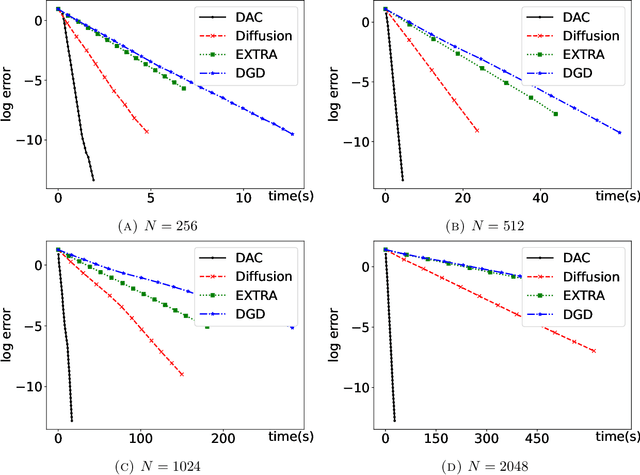
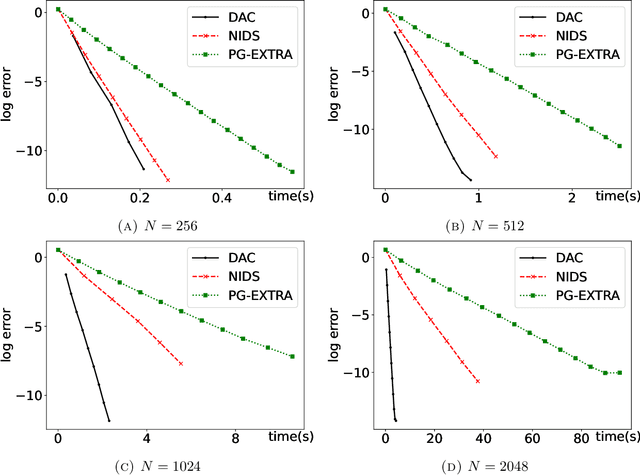
Abstract:In this paper, we consider networks with topologies described by some connected undirected graph ${\mathcal{G}}=(V, E)$ and with some agents (fusion centers) equipped with processing power and local peer-to-peer communication, and optimization problem $\min_{{\boldsymbol x}}\big\{F({\boldsymbol x})=\sum_{i\in V}f_i({\boldsymbol x})\big\}$ with local objective functions $f_i$ depending only on neighboring variables of the vertex $i\in V$. We introduce a divide-and-conquer algorithm to solve the above optimization problem in a distributed and decentralized manner. The proposed divide-and-conquer algorithm has exponential convergence, its computational cost is almost linear with respect to the size of the network, and it can be fully implemented at fusion centers of the network. Our numerical demonstrations also indicate that the proposed divide-and-conquer algorithm has superior performance than popular decentralized optimization methods do for the least squares problem with/without $\ell^1$ penalty.
PCM-TV-TFV: A Novel Two Stage Framework for Image Reconstruction from Fourier Data
May 29, 2017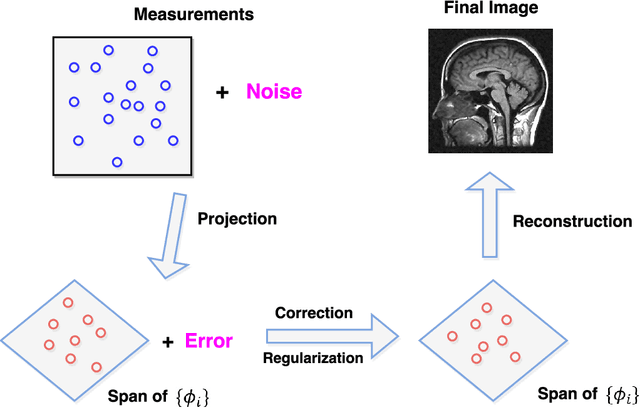
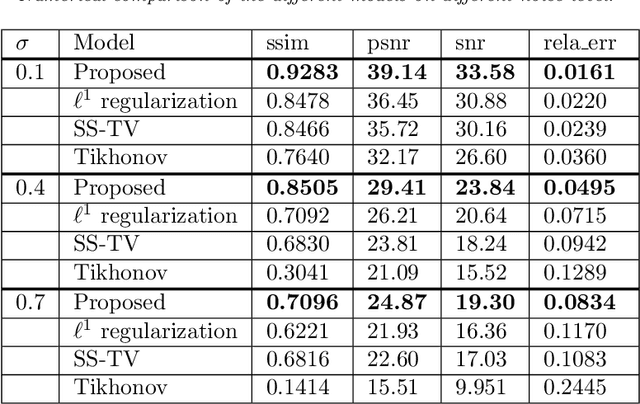
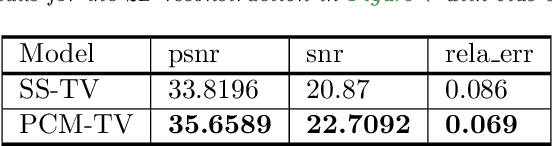
Abstract:We propose in this paper a novel two-stage Projection Correction Modeling (PCM) framework for image reconstruction from (non-uniform) Fourier measurements. PCM consists of a projection stage (P-stage) motivated by the multi-scale Galerkin method and a correction stage (C-stage) with an edge guided regularity fusing together the advantages of total variation (TV) and total fractional variation (TFV). The P-stage allows for continuous modeling of the underlying image of interest. The given measurements are projected onto a space in which the image is well represented. We then enhance the reconstruction result at the C-stage that minimizes an energy functional consisting of a fidelity in the transformed domain and a novel edge guided regularity. We further develop efficient proximal algorithms to solve the corresponding optimization problem. Various numerical results in both 1D signals and 2D images have also been presented to demonstrate the superior performance of the proposed two-stage method to other classical one-stage methods.
Reproducing Kernel Banach Spaces with the l1 Norm
Mar 28, 2012
Abstract:Targeting at sparse learning, we construct Banach spaces B of functions on an input space X with the properties that (1) B possesses an l1 norm in the sense that it is isometrically isomorphic to the Banach space of integrable functions on X with respect to the counting measure; (2) point evaluations are continuous linear functionals on B and are representable through a bilinear form with a kernel function; (3) regularized learning schemes on B satisfy the linear representer theorem. Examples of kernel functions admissible for the construction of such spaces are given.
* 28 pages, an extra section was added
Reproducing Kernel Banach Spaces with the l1 Norm II: Error Analysis for Regularized Least Square Regression
Jan 27, 2011Abstract:A typical approach in estimating the learning rate of a regularized learning scheme is to bound the approximation error by the sum of the sampling error, the hypothesis error and the regularization error. Using a reproducing kernel space that satisfies the linear representer theorem brings the advantage of discarding the hypothesis error from the sum automatically. Following this direction, we illustrate how reproducing kernel Banach spaces with the l1 norm can be applied to improve the learning rate estimate of l1-regularization in machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge