PCM-TV-TFV: A Novel Two Stage Framework for Image Reconstruction from Fourier Data
Paper and Code
May 29, 2017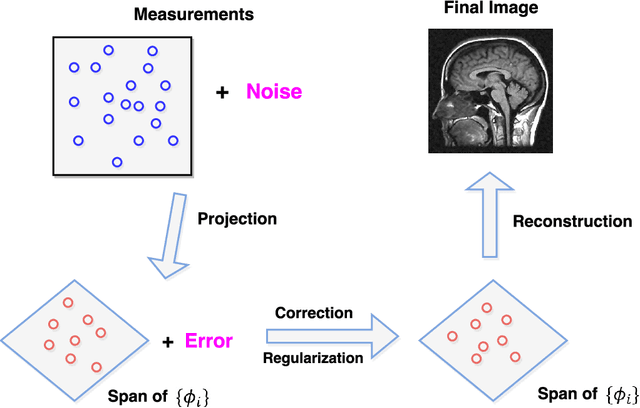
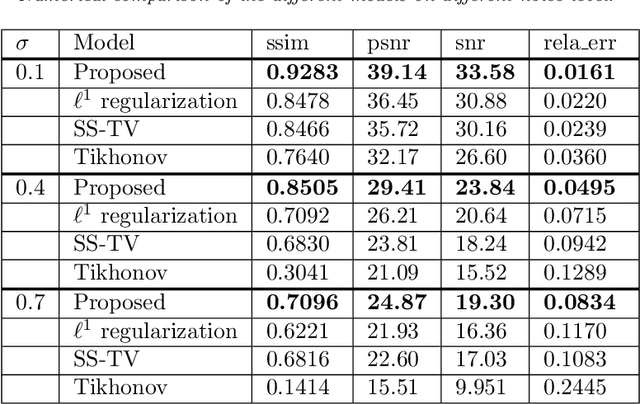
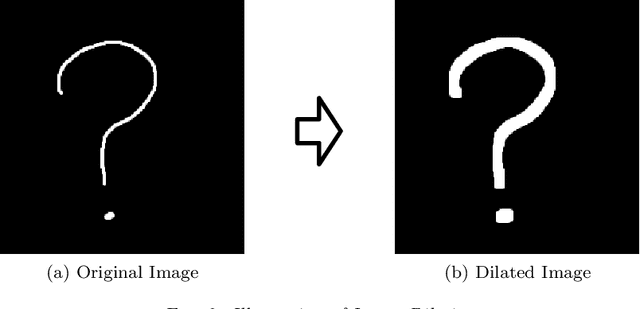
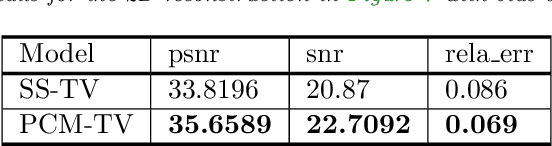
We propose in this paper a novel two-stage Projection Correction Modeling (PCM) framework for image reconstruction from (non-uniform) Fourier measurements. PCM consists of a projection stage (P-stage) motivated by the multi-scale Galerkin method and a correction stage (C-stage) with an edge guided regularity fusing together the advantages of total variation (TV) and total fractional variation (TFV). The P-stage allows for continuous modeling of the underlying image of interest. The given measurements are projected onto a space in which the image is well represented. We then enhance the reconstruction result at the C-stage that minimizes an energy functional consisting of a fidelity in the transformed domain and a novel edge guided regularity. We further develop efficient proximal algorithms to solve the corresponding optimization problem. Various numerical results in both 1D signals and 2D images have also been presented to demonstrate the superior performance of the proposed two-stage method to other classical one-stage methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge