MG-SpaIR: Multi-grade Sparse-guided Implicit Representation for Training-Data-Free Image Restoration

MG-SpaIR is a training-data-free framework for restoring a clean image from a single observation corrupted by a mixture of blur, downsampling, noise, and missing pixels. Building on implicit neural representations (INRs), we introduce a multi-grade coarse-to-fine residual hierarchy that progressively refines the reconstruction across resolution grades, improving representational fidelity and mitigating spectral limitations. To stabilize reconstruction optimization and suppress INR-induced artifacts, we further propose an explicit sparse proximal regularization (e.g., $\ell_0$-type) applied directly in the high-resolution image domain, which discourages spurious high-frequency patterns while preserving sharp structures. The resulting optimization is solved efficiently via a multi-grade proximal alternating scheme, and we establish convergence guarantees for the associated updates under standard regularity conditions. Experiments on mixed-degradation benchmarks demonstrate that MG-SpaIR consistently outperforms strong training-data-free baselines such as Deep Image Prior, providing a stable, interpretable, and data-efficient alternative to conventional learning-based restoration methods.

Oracle Supervision Transfers for Hyperparameter Prediction in Model-Based Image Denoising

Hyperparameter prediction is a critical practical bottleneck for model-based image denoisers, ranging from classical TV/TGV variational solvers to modern diffusion-based models such as DiffPIR. While existing learned predictors can achieve near-oracle performance, this approach scales poorly: each new configuration conventionally requires its own oracle-labeled training set, and each label requires a hierarchical grid search evaluated against clean ground truth. We therefore ask whether oracle supervision collected on source configurations can transfer to target configurations with few or no target oracle labels. We propose HyperDn, a single configuration-conditioned predictor that pools oracle supervision across source configurations and predicts heterogeneous hyperparameters for new denoiser--noise configurations. In a cross-paradigm experiment, HyperDn transfers from relatively cheap TV/TGV variational sources to more expensive diffusion-based DiffPIR. With only $2$ target oracle labels, it reaches $30.23$\,dB, within $0.90$\,dB of the oracle, and outperforms the $64$-label per-configuration predictor trained from scratch, using $1/32$ as many target labels as that baseline point. Without any target oracle labels, HyperDn also reaches near-oracle PSNR on two unseen mixtures of seen noise types and on transfer from relatively cheap $96\times 96$ source images to $512\times 768$ targets. Together, these results show that expensive oracle supervision for hyperparameter prediction can be transferred from source to new target configurations, reducing the need to rebuild oracle labels for each new denoising configuration.

Signal and Image Recovery with Scale and Signed Permutation Invariant Sparsity-Promoting Functions

Sparse signal recovery has been a cornerstone of advancements in data processing and imaging. Recently, the squared ratio of $\ell_1$ to $\ell_2$ norms, $(\ell_1/\ell_2)^2$, has been introduced as a sparsity-prompting function, showing superior performance compared to traditional $\ell_1$ minimization, particularly in challenging scenarios with high coherence and dynamic range. This paper explores the integration of the proximity operator of $(\ell_1/\ell_2)^2$ and $\ell_1/\ell_2$ into efficient optimization frameworks, including the Accelerated Proximal Gradient (APG) and Alternating Direction Method of Multipliers (ADMM). We rigorously analyze the convergence properties of these algorithms and demonstrate their effectiveness in compressed sensing and image restoration applications. Numerical experiments highlight the advantages of our proposed methods in terms of recovery accuracy and computational efficiency, particularly under noise and high-coherence conditions.

Sparse Deep Learning Models with the $\ell_1$ Regularization

Sparse neural networks are highly desirable in deep learning in reducing its complexity. The goal of this paper is to study how choices of regularization parameters influence the sparsity level of learned neural networks. We first derive the $\ell_1$-norm sparsity-promoting deep learning models including single and multiple regularization parameters models, from a statistical viewpoint. We then characterize the sparsity level of a regularized neural network in terms of the choice of the regularization parameters. Based on the characterizations, we develop iterative algorithms for selecting regularization parameters so that the weight parameters of the resulting deep neural network enjoy prescribed sparsity levels. Numerical experiments are presented to demonstrate the effectiveness of the proposed algorithms in choosing desirable regularization parameters and obtaining corresponding neural networks having both of predetermined sparsity levels and satisfactory approximation accuracy.

Large-Scale Non-convex Stochastic Constrained Distributionally Robust Optimization

Distributionally robust optimization (DRO) is a powerful framework for training robust models against data distribution shifts. This paper focuses on constrained DRO, which has an explicit characterization of the robustness level. Existing studies on constrained DRO mostly focus on convex loss function, and exclude the practical and challenging case with non-convex loss function, e.g., neural network. This paper develops a stochastic algorithm and its performance analysis for non-convex constrained DRO. The computational complexity of our stochastic algorithm at each iteration is independent of the overall dataset size, and thus is suitable for large-scale applications. We focus on the general Cressie-Read family divergence defined uncertainty set which includes $\chi^2$-divergences as a special case. We prove that our algorithm finds an $\epsilon$-stationary point with a computational complexity of $\mathcal O(\epsilon^{-3k_*-5})$, where $k_*$ is the parameter of the Cressie-Read divergence. The numerical results indicate that our method outperforms existing methods.} Our method also applies to the smoothed conditional value at risk (CVaR) DRO.

Hyperparameter Estimation for Sparse Bayesian Learning Models

Sparse Bayesian Learning (SBL) models are extensively used in signal processing and machine learning for promoting sparsity through hierarchical priors. The hyperparameters in SBL models are crucial for the model's performance, but they are often difficult to estimate due to the non-convexity and the high-dimensionality of the associated objective function. This paper presents a comprehensive framework for hyperparameter estimation in SBL models, encompassing well-known algorithms such as the expectation-maximization (EM), MacKay, and convex bounding (CB) algorithms. These algorithms are cohesively interpreted within an alternating minimization and linearization (AML) paradigm, distinguished by their unique linearized surrogate functions. Additionally, a novel algorithm within the AML framework is introduced, showing enhanced efficiency, especially under low signal noise ratios. This is further improved by a new alternating minimization and quadratic approximation (AMQ) paradigm, which includes a proximal regularization term. The paper substantiates these advancements with thorough convergence analysis and numerical experiments, demonstrating the algorithm's effectiveness in various noise conditions and signal-to-noise ratios.

Finding Dantzig selectors with a proximity operator based fixed-point algorithm

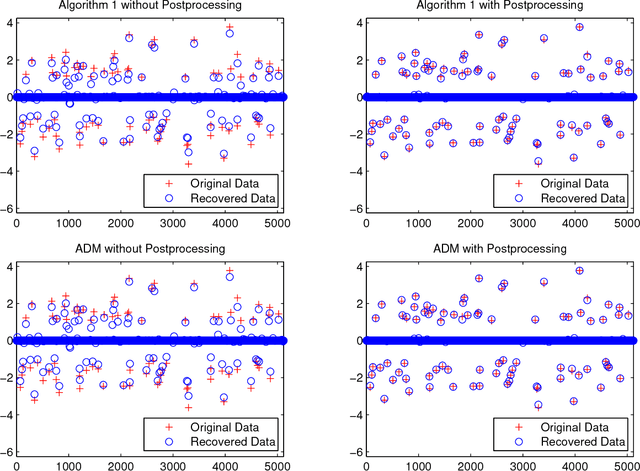
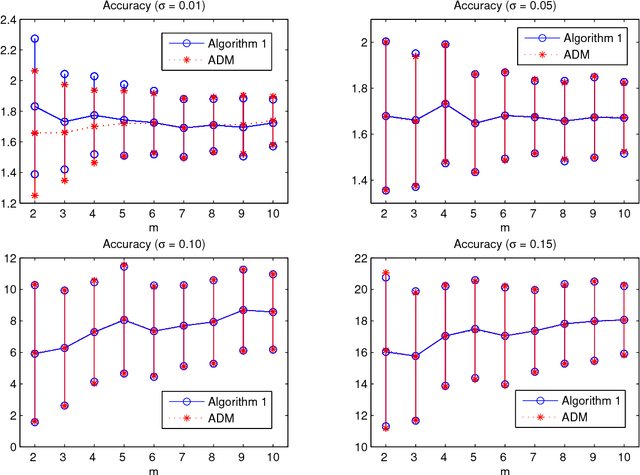
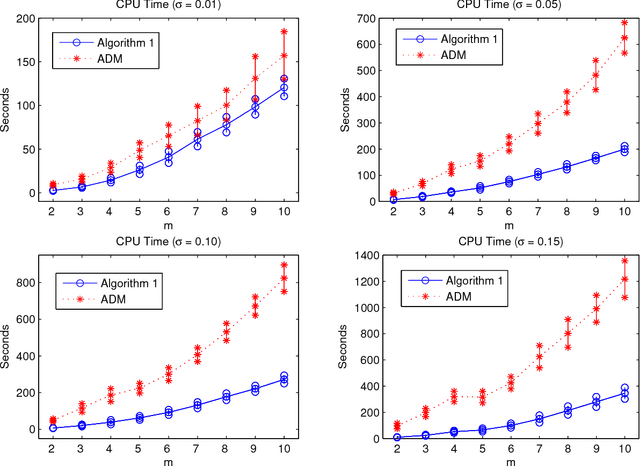
In this paper, we study a simple iterative method for finding the Dantzig selector, which was designed for linear regression problems. The method consists of two main stages. The first stage is to approximate the Dantzig selector through a fixed-point formulation of solutions to the Dantzig selector problem. The second stage is to construct a new estimator by regressing data onto the support of the approximated Dantzig selector. We compare our method to an alternating direction method, and present the results of numerical simulations using both the proposed method and the alternating direction method on synthetic and real data sets. The numerical simulations demonstrate that the two methods produce results of similar quality, however the proposed method tends to be significantly faster.

Separation of undersampled composite signals using the Dantzig selector with overcomplete dictionaries

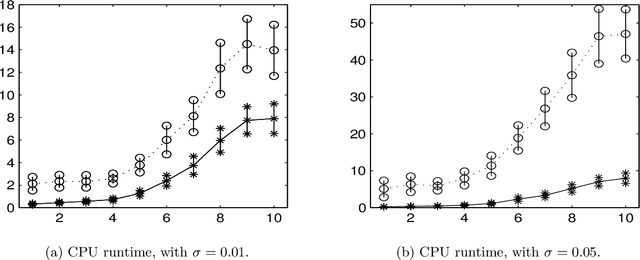
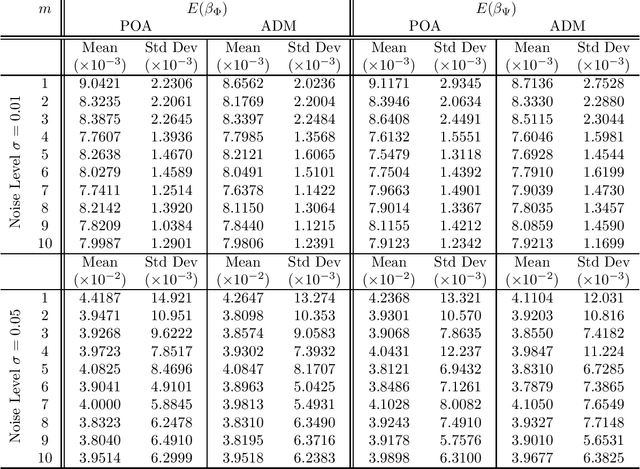
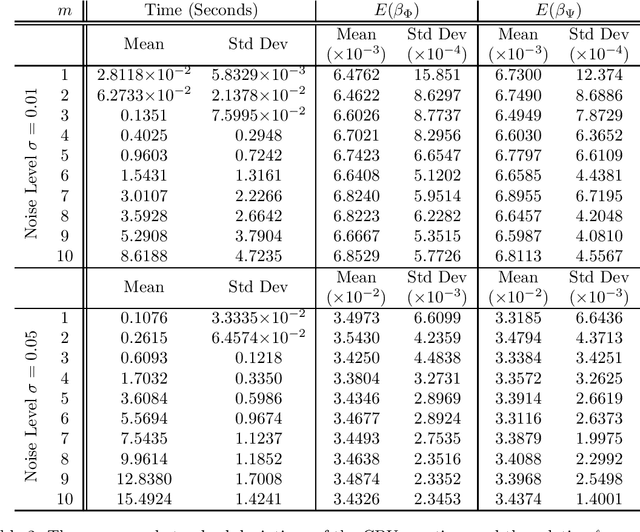
In many applications one may acquire a composition of several signals that may be corrupted by noise, and it is a challenging problem to reliably separate the components from one another without sacrificing significant details. Adding to the challenge, in a compressive sensing framework, one is given only an undersampled set of linear projections of the composite signal. In this paper, we propose using the Dantzig selector model incorporating an overcomplete dictionary to separate a noisy undersampled collection of composite signals, and present an algorithm to efficiently solve the model. The Dantzig selector is a statistical approach to finding a solution to a noisy linear regression problem by minimizing the $\ell_1$ norm of candidate coefficient vectors while constraining the scope of the residuals. If the underlying coefficient vector is sparse, then the Dantzig selector performs well in the recovery and separation of the unknown composite signal. In the following, we propose a proximity operator based algorithm to recover and separate unknown noisy undersampled composite signals through the Dantzig selector. We present numerical simulations comparing the proposed algorithm with the competing Alternating Direction Method, and the proposed algorithm is found to be faster, while producing similar quality results. Additionally, we demonstrate the utility of the proposed algorithm in several experiments by applying it in various domain applications including the recovery of complex-valued coefficient vectors, the removal of impulse noise from smooth signals, and the separation and classification of a composition of handwritten digits.

Efficient First Order Methods for Linear Composite Regularizers

A wide class of regularization problems in machine learning and statistics employ a regularization term which is obtained by composing a simple convex function \omega with a linear transformation. This setting includes Group Lasso methods, the Fused Lasso and other total variation methods, multi-task learning methods and many more. In this paper, we present a general approach for computing the proximity operator of this class of regularizers, under the assumption that the proximity operator of the function \omega is known in advance. Our approach builds on a recent line of research on optimal first order optimization methods and uses fixed point iterations for numerically computing the proximity operator. It is more general than current approaches and, as we show with numerical simulations, computationally more efficient than available first order methods which do not achieve the optimal rate. In particular, our method outperforms state of the art O(1/T) methods for overlapping Group Lasso and matches optimal O(1/T^2) methods for the Fused Lasso and tree structured Group Lasso.