Classification via Tensor Decompositions of Echo State Networks

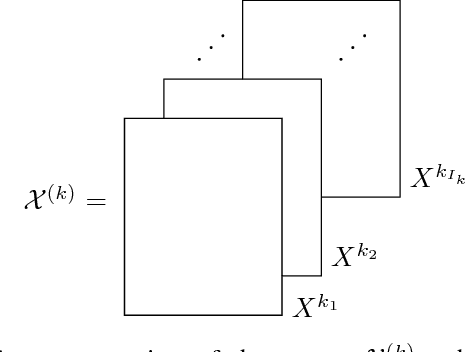
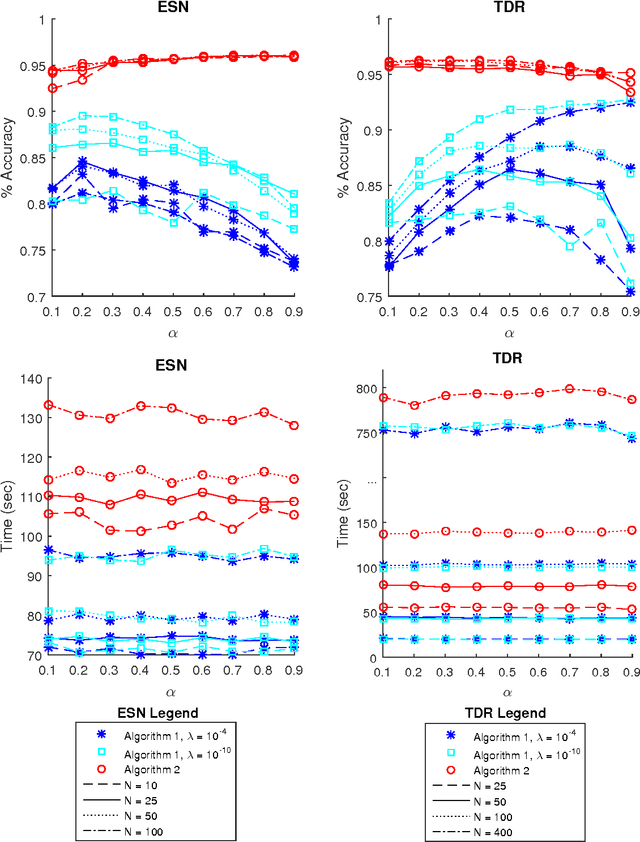
This work introduces a tensor-based method to perform supervised classification on spatiotemporal data processed in an echo state network. Typically when performing supervised classification tasks on data processed in an echo state network, the entire collection of hidden layer node states from the training dataset is shaped into a matrix, allowing one to use standard linear algebra techniques to train the output layer. However, the collection of hidden layer states is multidimensional in nature, and representing it as a matrix may lead to undesirable numerical conditions or loss of spatial and temporal correlations in the data. This work proposes a tensor-based supervised classification method on echo state network data that preserves and exploits the multidimensional nature of the hidden layer states. The method, which is based on orthogonal Tucker decompositions of tensors, is compared with the standard linear output weight approach in several numerical experiments on both synthetic and natural data. The results show that the tensor-based approach tends to outperform the standard approach in terms of classification accuracy.

Comparison of echo state network output layer classification methods on noisy data

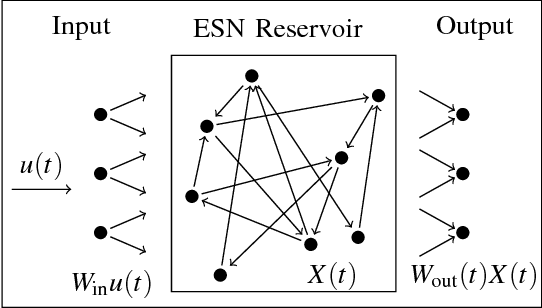
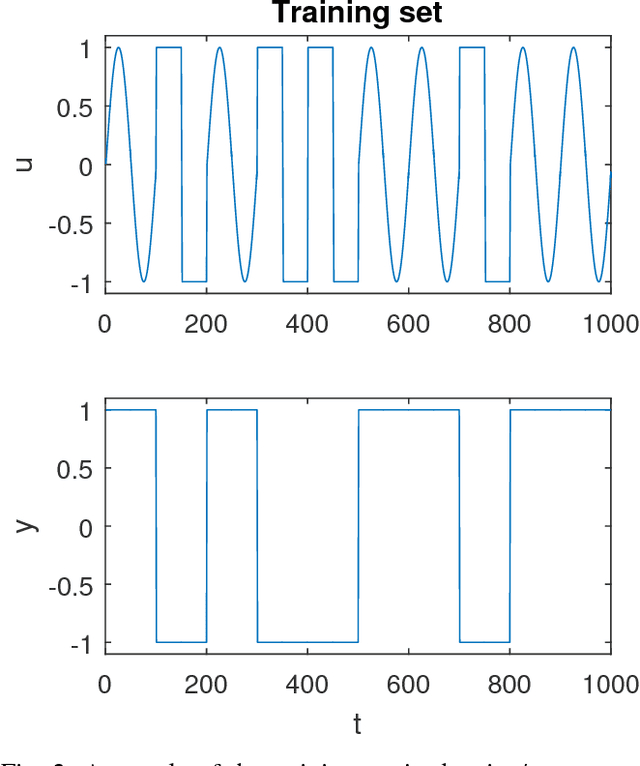
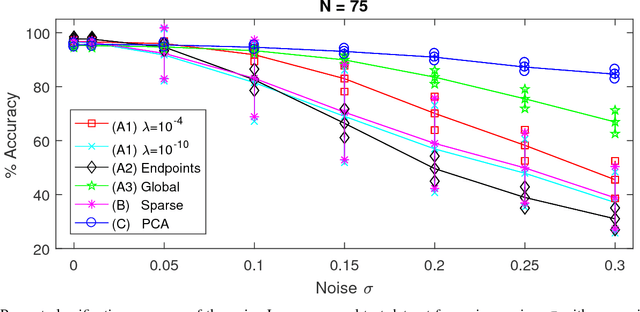
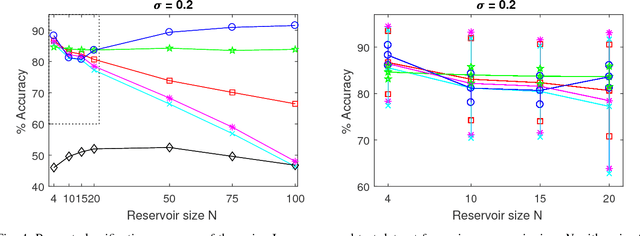
Echo state networks are a recently developed type of recurrent neural network where the internal layer is fixed with random weights, and only the output layer is trained on specific data. Echo state networks are increasingly being used to process spatiotemporal data in real-world settings, including speech recognition, event detection, and robot control. A strength of echo state networks is the simple method used to train the output layer - typically a collection of linear readout weights found using a least squares approach. Although straightforward to train and having a low computational cost to use, this method may not yield acceptable accuracy performance on noisy data. This study compares the performance of three echo state network output layer methods to perform classification on noisy data: using trained linear weights, using sparse trained linear weights, and using trained low-rank approximations of reservoir states. The methods are investigated experimentally on both synthetic and natural datasets. The experiments suggest that using regularized least squares to train linear output weights is superior on data with low noise, but using the low-rank approximations may significantly improve accuracy on datasets contaminated with higher noise levels.

Reservoir computing for spatiotemporal signal classification without trained output weights

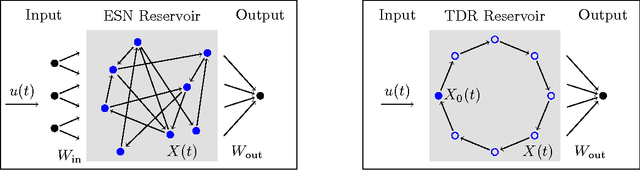
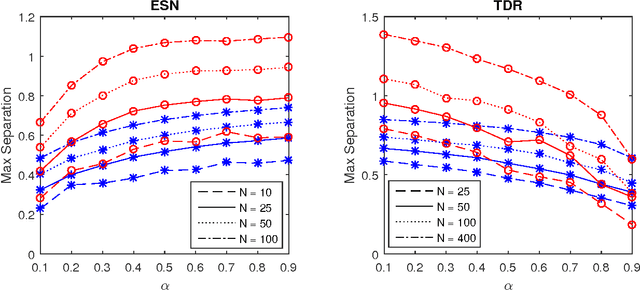
Reservoir computing is a recently introduced machine learning paradigm that has been shown to be well-suited for the processing of spatiotemporal data. Rather than training the network node connections and weights via backpropagation in traditional recurrent neural networks, reservoirs instead have fixed connections and weights among the `hidden layer' nodes, and traditionally only the weights to the output layer of neurons are trained using linear regression. We claim that for signal classification tasks one may forgo the weight training step entirely and instead use a simple supervised clustering method based upon principal components of norms of reservoir states. The proposed method is mathematically analyzed and explored through numerical experiments on real-world data. The examples demonstrate that the proposed may outperform the traditional trained output weight approach in terms of classification accuracy and sensitivity to reservoir parameters.

Finding Dantzig selectors with a proximity operator based fixed-point algorithm

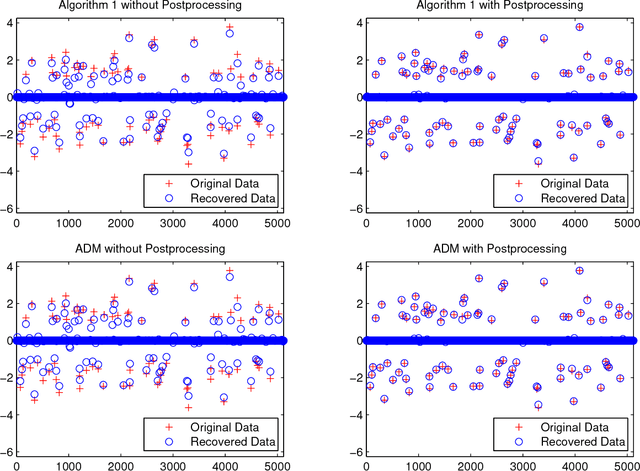
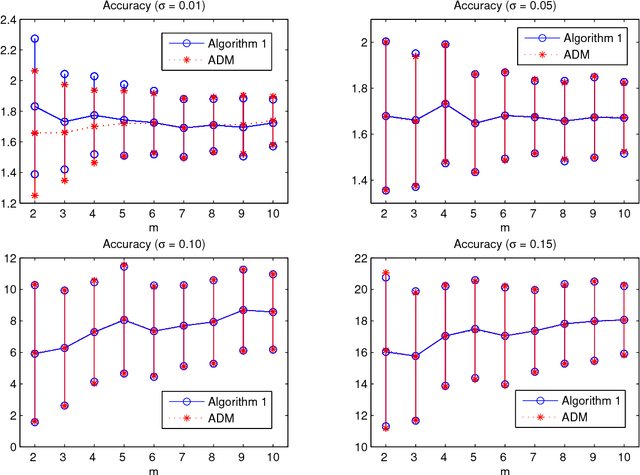
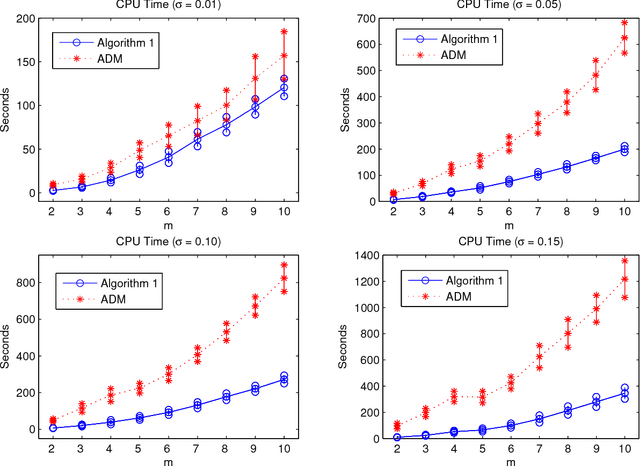
In this paper, we study a simple iterative method for finding the Dantzig selector, which was designed for linear regression problems. The method consists of two main stages. The first stage is to approximate the Dantzig selector through a fixed-point formulation of solutions to the Dantzig selector problem. The second stage is to construct a new estimator by regressing data onto the support of the approximated Dantzig selector. We compare our method to an alternating direction method, and present the results of numerical simulations using both the proposed method and the alternating direction method on synthetic and real data sets. The numerical simulations demonstrate that the two methods produce results of similar quality, however the proposed method tends to be significantly faster.

Separation of undersampled composite signals using the Dantzig selector with overcomplete dictionaries

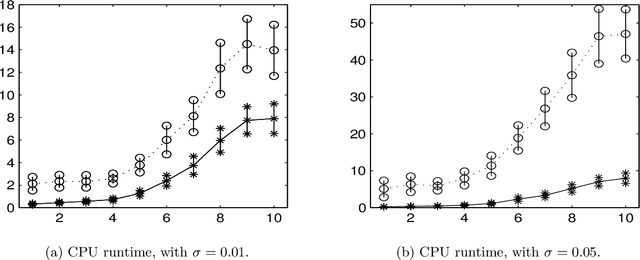
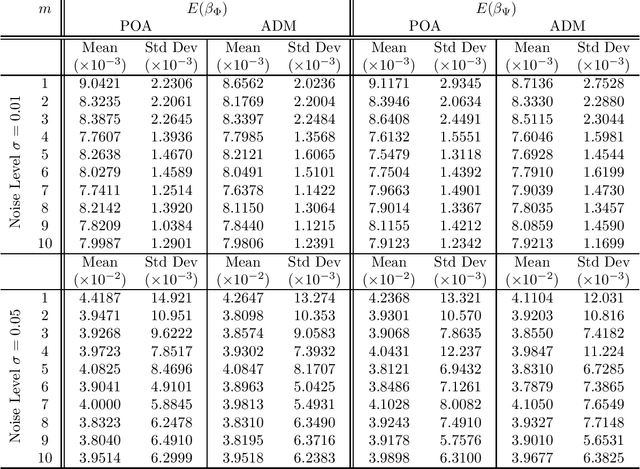
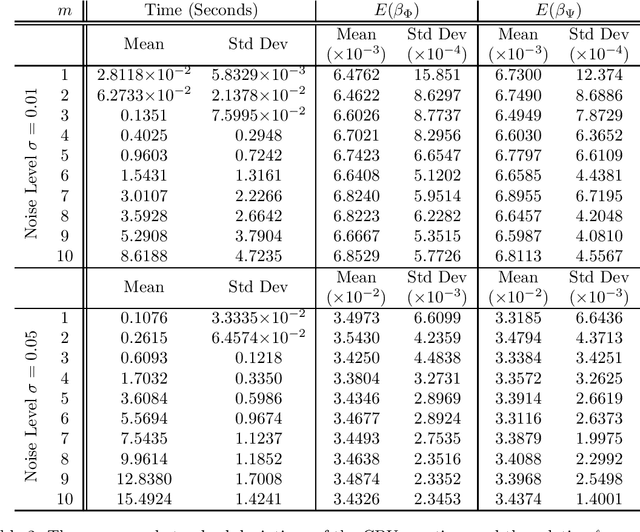
In many applications one may acquire a composition of several signals that may be corrupted by noise, and it is a challenging problem to reliably separate the components from one another without sacrificing significant details. Adding to the challenge, in a compressive sensing framework, one is given only an undersampled set of linear projections of the composite signal. In this paper, we propose using the Dantzig selector model incorporating an overcomplete dictionary to separate a noisy undersampled collection of composite signals, and present an algorithm to efficiently solve the model. The Dantzig selector is a statistical approach to finding a solution to a noisy linear regression problem by minimizing the $\ell_1$ norm of candidate coefficient vectors while constraining the scope of the residuals. If the underlying coefficient vector is sparse, then the Dantzig selector performs well in the recovery and separation of the unknown composite signal. In the following, we propose a proximity operator based algorithm to recover and separate unknown noisy undersampled composite signals through the Dantzig selector. We present numerical simulations comparing the proposed algorithm with the competing Alternating Direction Method, and the proposed algorithm is found to be faster, while producing similar quality results. Additionally, we demonstrate the utility of the proposed algorithm in several experiments by applying it in various domain applications including the recovery of complex-valued coefficient vectors, the removal of impulse noise from smooth signals, and the separation and classification of a composition of handwritten digits.