Separation of undersampled composite signals using the Dantzig selector with overcomplete dictionaries

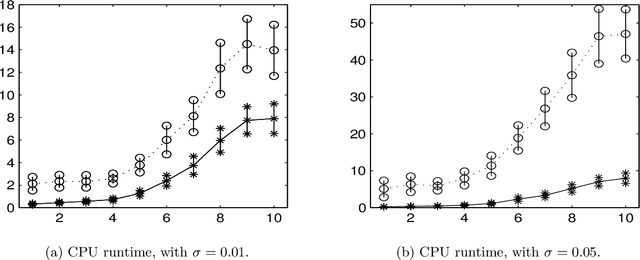
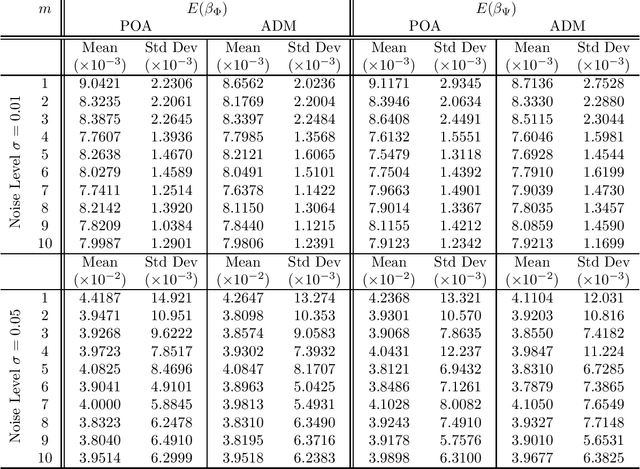
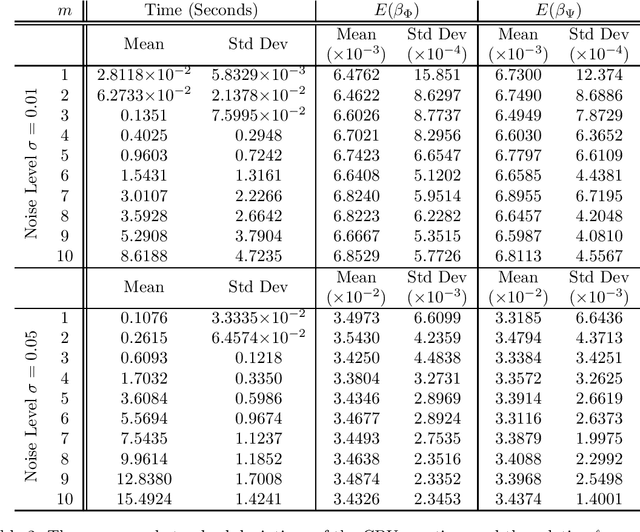
In many applications one may acquire a composition of several signals that may be corrupted by noise, and it is a challenging problem to reliably separate the components from one another without sacrificing significant details. Adding to the challenge, in a compressive sensing framework, one is given only an undersampled set of linear projections of the composite signal. In this paper, we propose using the Dantzig selector model incorporating an overcomplete dictionary to separate a noisy undersampled collection of composite signals, and present an algorithm to efficiently solve the model. The Dantzig selector is a statistical approach to finding a solution to a noisy linear regression problem by minimizing the $\ell_1$ norm of candidate coefficient vectors while constraining the scope of the residuals. If the underlying coefficient vector is sparse, then the Dantzig selector performs well in the recovery and separation of the unknown composite signal. In the following, we propose a proximity operator based algorithm to recover and separate unknown noisy undersampled composite signals through the Dantzig selector. We present numerical simulations comparing the proposed algorithm with the competing Alternating Direction Method, and the proposed algorithm is found to be faster, while producing similar quality results. Additionally, we demonstrate the utility of the proposed algorithm in several experiments by applying it in various domain applications including the recovery of complex-valued coefficient vectors, the removal of impulse noise from smooth signals, and the separation and classification of a composition of handwritten digits.