Finding Dantzig selectors with a proximity operator based fixed-point algorithm
Paper and Code
Feb 19, 2015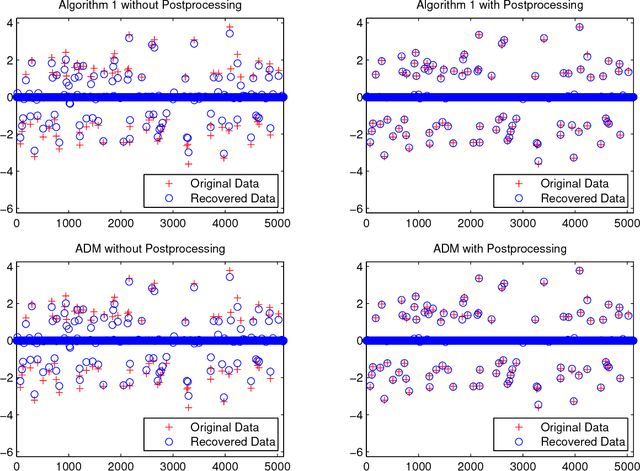
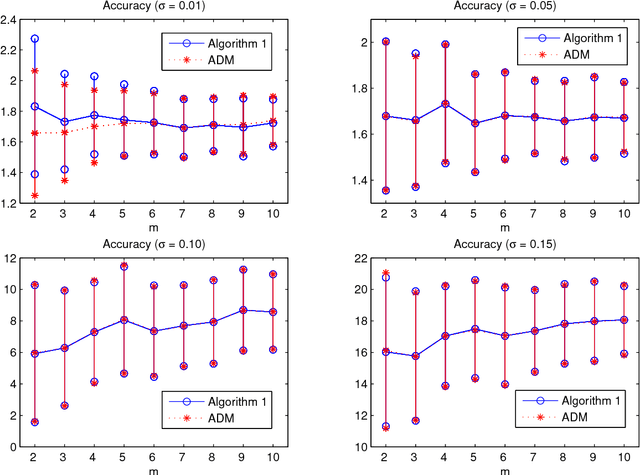
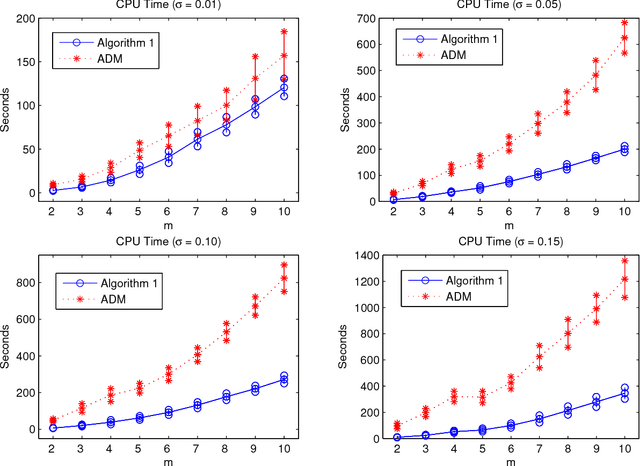

In this paper, we study a simple iterative method for finding the Dantzig selector, which was designed for linear regression problems. The method consists of two main stages. The first stage is to approximate the Dantzig selector through a fixed-point formulation of solutions to the Dantzig selector problem. The second stage is to construct a new estimator by regressing data onto the support of the approximated Dantzig selector. We compare our method to an alternating direction method, and present the results of numerical simulations using both the proposed method and the alternating direction method on synthetic and real data sets. The numerical simulations demonstrate that the two methods produce results of similar quality, however the proposed method tends to be significantly faster.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge