A Divide-and-Conquer Algorithm for Distributed Optimization on Networks
Paper and Code
Dec 03, 2021
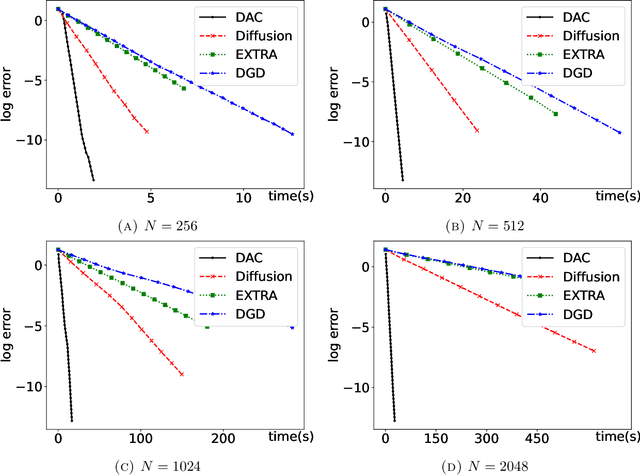
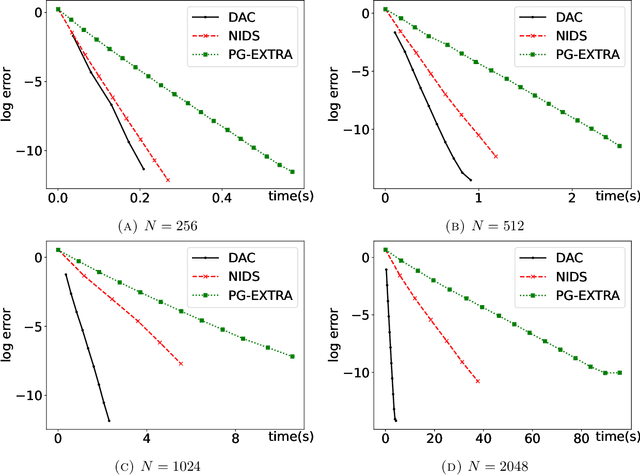
In this paper, we consider networks with topologies described by some connected undirected graph ${\mathcal{G}}=(V, E)$ and with some agents (fusion centers) equipped with processing power and local peer-to-peer communication, and optimization problem $\min_{{\boldsymbol x}}\big\{F({\boldsymbol x})=\sum_{i\in V}f_i({\boldsymbol x})\big\}$ with local objective functions $f_i$ depending only on neighboring variables of the vertex $i\in V$. We introduce a divide-and-conquer algorithm to solve the above optimization problem in a distributed and decentralized manner. The proposed divide-and-conquer algorithm has exponential convergence, its computational cost is almost linear with respect to the size of the network, and it can be fully implemented at fusion centers of the network. Our numerical demonstrations also indicate that the proposed divide-and-conquer algorithm has superior performance than popular decentralized optimization methods do for the least squares problem with/without $\ell^1$ penalty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge