Entropy stable conservative flux form neural networks

We propose an entropy-stable conservative flux form neural network (CFN) that integrates classical numerical conservation laws into a data-driven framework using the entropy-stable, second-order, and non-oscillatory Kurganov-Tadmor (KT) scheme. The proposed entropy-stable CFN uses slope limiting as a denoising mechanism, ensuring accurate predictions in both noisy and sparse observation environments, as well as in both smooth and discontinuous regions. Numerical experiments demonstrate that the entropy-stable CFN achieves both stability and conservation while maintaining accuracy over extended time domains. Furthermore, it successfully predicts shock propagation speeds in long-term simulations, {\it without} oracle knowledge of later-time profiles in the training data.

Learning In-between Imagery Dynamics via Physical Latent Spaces

We present a framework designed to learn the underlying dynamics between two images observed at consecutive time steps. The complex nature of image data and the lack of temporal information pose significant challenges in capturing the unique evolving patterns. Our proposed method focuses on estimating the intermediary stages of image evolution, allowing for interpretability through latent dynamics while preserving spatial correlations with the image. By incorporating a latent variable that follows a physical model expressed in partial differential equations (PDEs), our approach ensures the interpretability of the learned model and provides insight into corresponding image dynamics. We demonstrate the robustness and effectiveness of our learning framework through a series of numerical tests using geoscientific imagery data.

Leveraging joint sparsity in hierarchical Bayesian learning

We present a hierarchical Bayesian learning approach to infer jointly sparse parameter vectors from multiple measurement vectors. Our model uses separate conditionally Gaussian priors for each parameter vector and common gamma-distributed hyper-parameters to enforce joint sparsity. The resulting joint-sparsity-promoting priors are combined with existing Bayesian inference methods to generate a new family of algorithms. Our numerical experiments, which include a multi-coil magnetic resonance imaging application, demonstrate that our new approach consistently outperforms commonly used hierarchical Bayesian methods.

Sequential edge detection using joint hierarchical Bayesian learning

This paper introduces a new sparse Bayesian learning (SBL) algorithm that jointly recovers a temporal sequence of edge maps from noisy and under-sampled Fourier data. The new method is cast in a Bayesian framework and uses a prior that simultaneously incorporates intra-image information to promote sparsity in each individual edge map with inter-image information to promote similarities in any unchanged regions. By treating both the edges as well as the similarity between adjacent images as random variables, there is no need to separately form regions of change. Thus we avoid both additional computational cost as well as any information loss resulting from pre-processing the image. Our numerical examples demonstrate that our new method compares favorably with more standard SBL approaches.

Sub-aperture SAR Imaging with Uncertainty Quantification

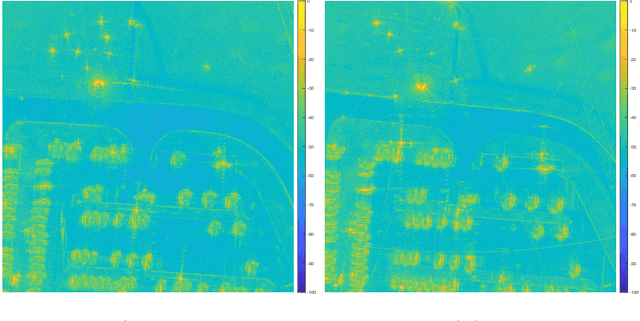
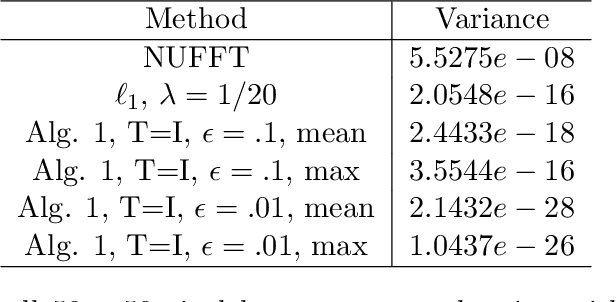
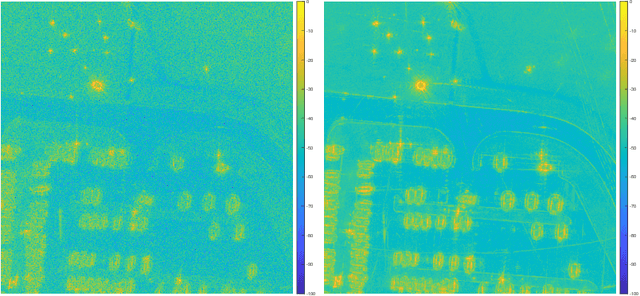
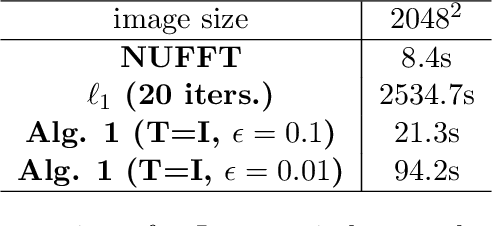
In the problem of spotlight mode airborne synthetic aperture radar (SAR) image formation, it is well-known that data collected over a wide azimuthal angle violate the isotropic scattering property typically assumed. Many techniques have been proposed to account for this issue, including both full-aperture and sub-aperture methods based on filtering, regularized least squares, and Bayesian methods. A full-aperture method that uses a hierarchical Bayesian prior to incorporate appropriate speckle modeling and reduction was recently introduced to produce samples of the posterior density rather than a single image estimate. This uncertainty quantification information is more robust as it can generate a variety of statistics for the scene. As proposed, the method was not well-suited for large problems, however, as the sampling was inefficient. Moreover, the method was not explicitly designed to mitigate the effects of the faulty isotropic scattering assumption. In this work we therefore propose a new sub-aperture SAR imaging method that uses a sparse Bayesian learning-type algorithm to more efficiently produce approximate posterior densities for each sub-aperture window. These estimates may be useful in and of themselves, or when of interest, the statistics from these distributions can be combined to form a composite image. Furthermore, unlike the often-employed lp-regularized least squares methods, no user-defined parameters are required. Application-specific adjustments are made to reduce the typically burdensome runtime and storage requirements so that appropriately large images can be generated. Finally, this paper focuses on incorporating these techniques into SAR image formation process. That is, for the problem starting with SAR phase history data, so that no additional processing errors are incurred.

Using Frame Theoretic Convolutional Gridding for Robust Synthetic Aperture Sonar Imaging

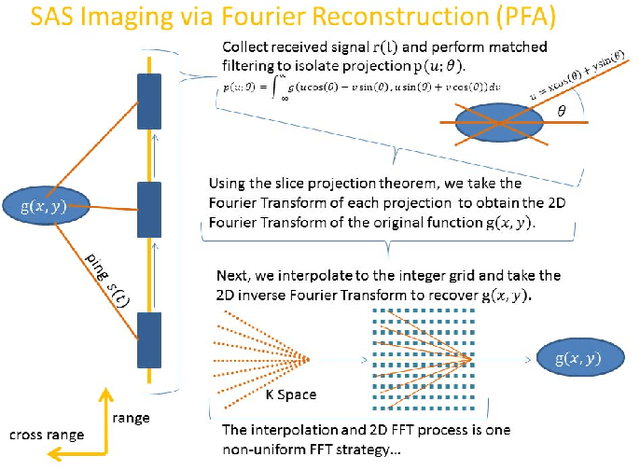
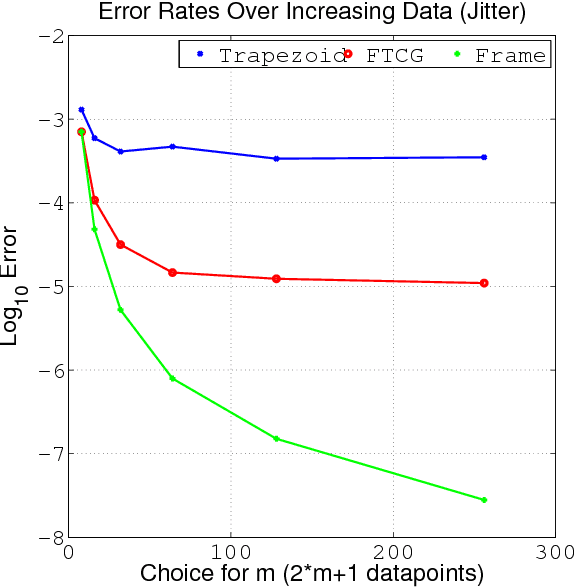
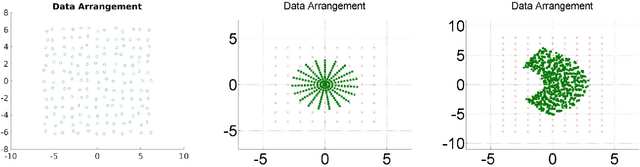
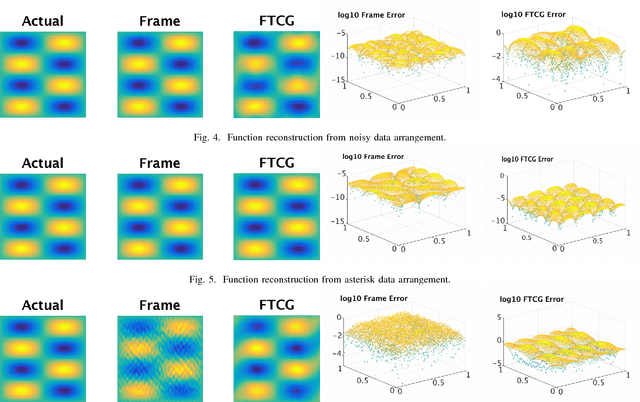
Recent progress in synthetic aperture sonar (SAS) technology and processing has led to significant advances in underwater imaging, outperforming previously common approaches in both accuracy and efficiency. There are, however, inherent limitations to current SAS reconstruction methodology. In particular, popular and efficient Fourier domain SAS methods require a 2D interpolation which is often ill conditioned and inaccurate, inevitably reducing robustness with regard to speckle and inaccurate sound-speed estimation. To overcome these issues, we propose using the frame theoretic convolution gridding (FTCG) algorithm to handle the non-uniform Fourier data. FTCG extends upon non-uniform fast Fourier transform (NUFFT) algorithms by casting the NUFFT as an approximation problem given Fourier frame data. The FTCG has been show to yield improved accuracy at little more computational cost. Using simulated data, we outline how the FTCG can be used to enhance current SAS processing.