Scoop-and-Toss: Dynamic Object Collection for Quadrupedal Systems

Quadruped robots have made significant advances in locomotion, extending their capabilities from controlled environments to real-world applications. Beyond movement, recent work has explored loco-manipulation using the legs to perform tasks such as pressing buttons or opening doors. While these efforts demonstrate the feasibility of leg-based manipulation, most have focused on relatively static tasks. In this work, we propose a framework that enables quadruped robots to collect objects without additional actuators by leveraging the agility of their legs. By attaching a simple scoop-like add-on to one leg, the robot can scoop objects and toss them into a collection tray mounted on its back. Our method employs a hierarchical policy structure comprising two expert policies-one for scooping and tossing, and one for approaching object positions-and a meta-policy that dynamically switches between them. The expert policies are trained separately, followed by meta-policy training for coordinated multi-object collection. This approach demonstrates how quadruped legs can be effectively utilized for dynamic object manipulation, expanding their role beyond locomotion.

Invariant Representations via Wasserstein Correlation Maximization

This work investigates the use of Wasserstein correlation -- a normalized measure of statistical dependence based on the Wasserstein distance between a joint distribution and the product of its marginals -- for unsupervised representation learning. Unlike, for example, contrastive methods, which naturally cluster classes in the latent space, we find that an (auto)encoder trained to maximize Wasserstein correlation between the input and encoded distributions instead acts as a compressor, reducing dimensionality while approximately preserving the topological and geometric properties of the input distribution. More strikingly, we show that Wasserstein correlation maximization can be used to arrive at an (auto)encoder -- either trained from scratch, or else one that extends a frozen, pretrained model -- that is approximately invariant to a chosen augmentation, or collection of augmentations, and that still approximately preserves the structural properties of the non-augmented input distribution. To do this, we first define the notion of an augmented encoder using the machinery of Markov-Wasserstein kernels. When the maximization objective is then applied to the augmented encoder, as opposed to the underlying, deterministic encoder, the resulting model exhibits the desired invariance properties. Finally, besides our experimental results, which show that even simple feedforward networks can be imbued with invariants or can, alternatively, be used to impart invariants to pretrained models under this training process, we additionally establish various theoretical results for optimal transport-based dependence measures. Code is available at https://github.com/keenan-eikenberry/wasserstein_correlation_maximization .

PhysicsFC: Learning User-Controlled Skills for a Physics-Based Football Player Controller

We propose PhysicsFC, a method for controlling physically simulated football player characters to perform a variety of football skills--such as dribbling, trapping, moving, and kicking--based on user input, while seamlessly transitioning between these skills. Our skill-specific policies, which generate latent variables for each football skill, are trained using an existing physics-based motion embedding model that serves as a foundation for reproducing football motions. Key features include a tailored reward design for the Dribble policy, a two-phase reward structure combined with projectile dynamics-based initialization for the Trap policy, and a Data-Embedded Goal-Conditioned Latent Guidance (DEGCL) method for the Move policy. Using the trained skill policies, the proposed football player finite state machine (PhysicsFC FSM) allows users to interactively control the character. To ensure smooth and agile transitions between skill policies, as defined in the FSM, we introduce the Skill Transition-Based Initialization (STI), which is applied during the training of each skill policy. We develop several interactive scenarios to showcase PhysicsFC's effectiveness, including competitive trapping and dribbling, give-and-go plays, and 11v11 football games, where multiple PhysicsFC agents produce natural and controllable physics-based football player behaviors. Quantitative evaluations further validate the performance of individual skill policies and the transitions between them, using the presented metrics and experimental designs.

Nonlinear Bayesian Update via Ensemble Kernel Regression with Clustering and Subsampling

Nonlinear Bayesian update for a prior ensemble is proposed to extend traditional ensemble Kalman filtering to settings characterized by non-Gaussian priors and nonlinear measurement operators. In this framework, the observed component is first denoised via a standard Kalman update, while the unobserved component is estimated using a nonlinear regression approach based on kernel density estimation. The method incorporates a subsampling strategy to ensure stability and, when necessary, employs unsupervised clustering to refine the conditional estimate. Numerical experiments on Lorenz systems and a PDE-constrained inverse problem illustrate that the proposed nonlinear update can reduce estimation errors compared to standard linear updates, especially in highly nonlinear scenarios.

Entropy stable conservative flux form neural networks

We propose an entropy-stable conservative flux form neural network (CFN) that integrates classical numerical conservation laws into a data-driven framework using the entropy-stable, second-order, and non-oscillatory Kurganov-Tadmor (KT) scheme. The proposed entropy-stable CFN uses slope limiting as a denoising mechanism, ensuring accurate predictions in both noisy and sparse observation environments, as well as in both smooth and discontinuous regions. Numerical experiments demonstrate that the entropy-stable CFN achieves both stability and conservation while maintaining accuracy over extended time domains. Furthermore, it successfully predicts shock propagation speeds in long-term simulations, {\it without} oracle knowledge of later-time profiles in the training data.

RARe: Retrieval Augmented Retrieval with In-Context Examples

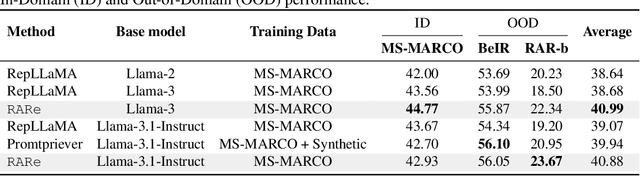
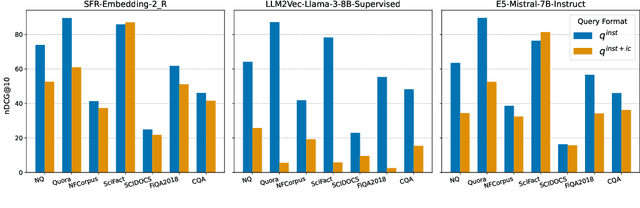
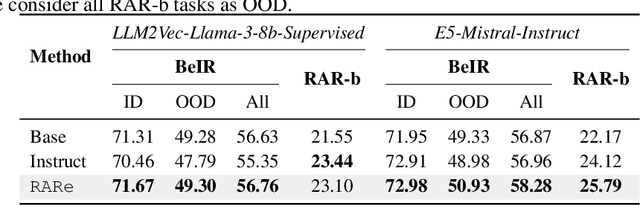
We investigate whether in-context examples, widely used in decoder-only language models (LLMs), can improve embedding model performance in retrieval tasks. Unlike in LLMs, naively prepending in-context examples (query-document pairs) to the target query at inference time does not work out of the box. We introduce a simple approach to enable retrievers to use in-context examples. Our approach, RARe, finetunes a pre-trained model with in-context examples whose query is semantically similar to the target query. This can be applied to adapt various base architectures (i.e., decoder-only language models, retriever models) and consistently achieves performance gains of up to +2.72% nDCG across various open-domain retrieval datasets (BeIR, RAR-b). In particular, we find RARe exhibits stronger out-of-domain generalization compared to models using queries without in-context examples, similar to what is seen for in-context learning in LLMs. We further provide analysis on the design choices of in-context example augmentation and lay the foundation for future work in this space.

Disentangling Questions from Query Generation for Task-Adaptive Retrieval

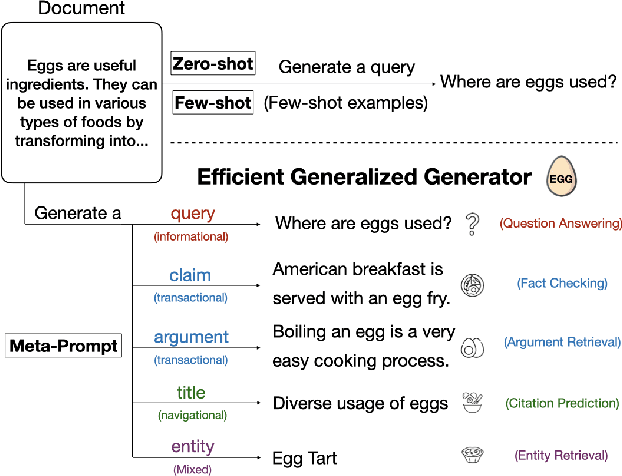
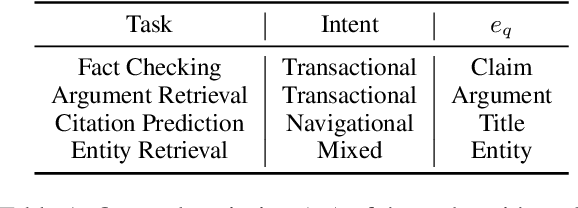
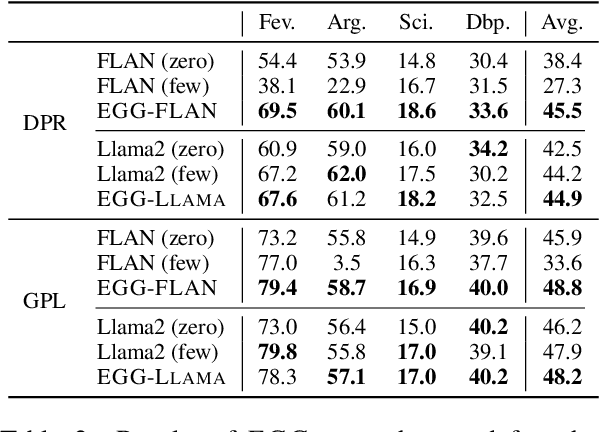
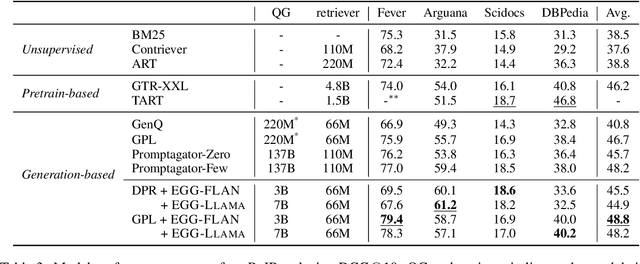
This paper studies the problem of information retrieval, to adapt to unseen tasks. Existing work generates synthetic queries from domain-specific documents to jointly train the retriever. However, the conventional query generator assumes the query as a question, thus failing to accommodate general search intents. A more lenient approach incorporates task-adaptive elements, such as few-shot learning with an 137B LLM. In this paper, we challenge a trend equating query and question, and instead conceptualize query generation task as a "compilation" of high-level intent into task-adaptive query. Specifically, we propose EGG, a query generator that better adapts to wide search intents expressed in the BeIR benchmark. Our method outperforms baselines and existing models on four tasks with underexplored intents, while utilizing a query generator 47 times smaller than the previous state-of-the-art. Our findings reveal that instructing the LM with explicit search intent is a key aspect of modeling an effective query generator.

AmbigDocs: Reasoning across Documents on Different Entities under the Same Name

Different entities with the same name can be difficult to distinguish. Handling confusing entity mentions is a crucial skill for language models (LMs). For example, given the question "Where was Michael Jordan educated?" and a set of documents discussing different people named Michael Jordan, can LMs distinguish entity mentions to generate a cohesive answer to the question? To test this ability, we introduce a new benchmark, AmbigDocs. By leveraging Wikipedia's disambiguation pages, we identify a set of documents, belonging to different entities who share an ambiguous name. From these documents, we generate questions containing an ambiguous name and their corresponding sets of answers. Our analysis reveals that current state-of-the-art models often yield ambiguous answers or incorrectly merge information belonging to different entities. We establish an ontology categorizing four types of incomplete answers and automatic evaluation metrics to identify such categories. We lay the foundation for future work on reasoning across multiple documents with ambiguous entities.

Stochastic approach for elliptic problems in perforated domains

A wide range of applications in science and engineering involve a PDE model in a domain with perforations, such as perforated metals or air filters. Solving such perforated domain problems suffers from computational challenges related to resolving the scale imposed by the geometries of perforations. We propose a neural network-based mesh-free approach for perforated domain problems. The method is robust and efficient in capturing various configuration scales, including the averaged macroscopic behavior of the solution that involves a multiscale nature induced by small perforations. The new approach incorporates the derivative-free loss method that uses a stochastic representation or the Feynman-Kac formulation. In particular, we implement the Neumann boundary condition for the derivative-free loss method to handle the interface between the domain and perforations. A suite of stringent numerical tests is provided to support the proposed method's efficacy in handling various perforation scales.

Crafting In-context Examples according to LMs' Parametric Knowledge

In-context learning has been applied to knowledge-rich tasks such as question answering. In such scenarios, in-context examples are used to trigger a behaviour in the language model: namely, it should surface information stored in its parametric knowledge. We study the construction of in-context example sets, with a focus on the parametric knowledge of the model regarding in-context examples. We identify 'known' examples, where models can correctly answer from its parametric knowledge, and 'unknown' ones. Our experiments show that prompting with 'unknown' examples decreases the performance, potentially as it encourages hallucination rather than searching its parametric knowledge. Constructing an in-context example set that presents both known and unknown information performs the best across diverse settings. We perform analysis on three multi-answer question answering datasets, which allows us to further study answer set ordering strategies based on the LM's knowledge about each answer. Together, our study sheds lights on how to best construct in-context example sets for knowledge-rich tasks.