Neural Entropy-stable conservative flux form neural networks for learning hyperbolic conservation laws

We propose a neural entropy-stable conservative flux form neural network (NESCFN) for learning hyperbolic conservation laws and their associated entropy functions directly from solution trajectories, without requiring any predefined numerical discretization. While recent neural network architectures have successfully integrated classical numerical principles into learned models, most rely on prior knowledge of the governing equations or assume a fixed discretization. Our approach removes this dependency by embedding entropy-stable design principles into the learning process itself, enabling the discovery of physically consistent dynamics in a fully data-driven setting. By jointly learning both the numerical flux function and a corresponding entropy, the proposed method ensures conservation and entropy dissipation, critical for long-term stability and fidelity in the system of hyperbolic conservation laws. Numerical results demonstrate that the method achieves stability and conservation over extended time horizons and accurately captures shock propagation speeds, even without oracle access to future-time solution profiles in the training data.

Invariant Representations via Wasserstein Correlation Maximization

This work investigates the use of Wasserstein correlation -- a normalized measure of statistical dependence based on the Wasserstein distance between a joint distribution and the product of its marginals -- for unsupervised representation learning. Unlike, for example, contrastive methods, which naturally cluster classes in the latent space, we find that an (auto)encoder trained to maximize Wasserstein correlation between the input and encoded distributions instead acts as a compressor, reducing dimensionality while approximately preserving the topological and geometric properties of the input distribution. More strikingly, we show that Wasserstein correlation maximization can be used to arrive at an (auto)encoder -- either trained from scratch, or else one that extends a frozen, pretrained model -- that is approximately invariant to a chosen augmentation, or collection of augmentations, and that still approximately preserves the structural properties of the non-augmented input distribution. To do this, we first define the notion of an augmented encoder using the machinery of Markov-Wasserstein kernels. When the maximization objective is then applied to the augmented encoder, as opposed to the underlying, deterministic encoder, the resulting model exhibits the desired invariance properties. Finally, besides our experimental results, which show that even simple feedforward networks can be imbued with invariants or can, alternatively, be used to impart invariants to pretrained models under this training process, we additionally establish various theoretical results for optimal transport-based dependence measures. Code is available at https://github.com/keenan-eikenberry/wasserstein_correlation_maximization .

Multi-scale DeepOnet (Mscale-DeepOnet) for Mitigating Spectral Bias in Learning High Frequency Operators of Oscillatory Functions

In this paper, a multi-scale DeepOnet (Mscale-DeepOnet) is proposed to reduce the spectral bias of the DeepOnet in learning high-frequency mapping between highly oscillatory functions, with an application to the nonlinear mapping between the coefficient of the Helmholtz equation and its solution. The Mscale-DeepOnet introduces the multiscale neural network in the branch and trunk networks of the original DeepOnet, the resulting Mscale-DeepOnet is shown to be able to capture various high-frequency components of the mapping itself and its image. Numerical results demonstrate the substantial improvement of the Mscale-DeepOnet for the problem of wave scattering in the high-frequency regime over the normal DeepOnet with a similar number of network parameters.

Entropy stable conservative flux form neural networks

We propose an entropy-stable conservative flux form neural network (CFN) that integrates classical numerical conservation laws into a data-driven framework using the entropy-stable, second-order, and non-oscillatory Kurganov-Tadmor (KT) scheme. The proposed entropy-stable CFN uses slope limiting as a denoising mechanism, ensuring accurate predictions in both noisy and sparse observation environments, as well as in both smooth and discontinuous regions. Numerical experiments demonstrate that the entropy-stable CFN achieves both stability and conservation while maintaining accuracy over extended time domains. Furthermore, it successfully predicts shock propagation speeds in long-term simulations, {\it without} oracle knowledge of later-time profiles in the training data.

A Phase Shift Deep Neural Network for High Frequency Wave Equations in Inhomogeneous Media

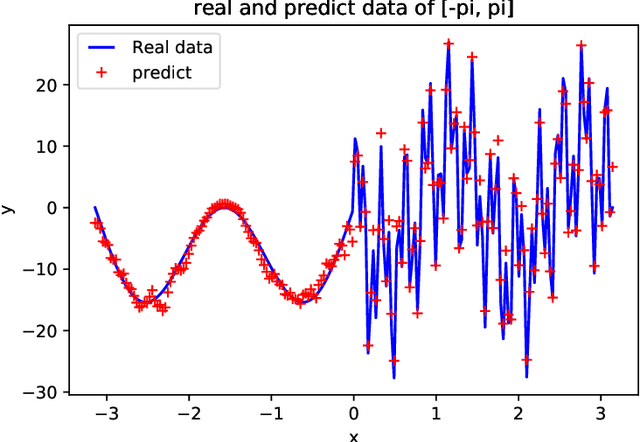
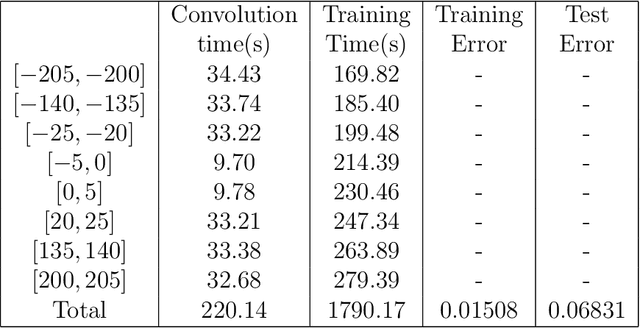
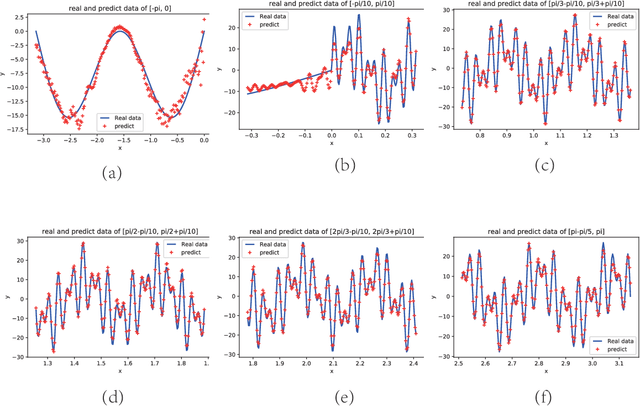
In this paper, we propose a phase shift deep neural network (PhaseDNN) which provides a wideband convergence in approximating high frequency solutions of wave equations. The PhaseDNN accounts for the fact that many DNN achieves convergence in the low frequency range first, a series of moderately-sized of DNNs are constructed and trained for selected high frequency ranges. With the help of phase shifts in the frequency domain, each DNN will be trained to approximate the target solution's higher frequency content over a specific range. Due to the phase shift, each DNN achieves the speed of convergence as in the low frequency range. As a result, the proposed PhaseDNN is able to convert high frequency learning to low frequency learning, thus allowing a uniform learning to wideband high frequency functions. The PhaseDNN will then be applied to find the solution of high frequency wave equations in inhomogeneous media. Numerical results have demonstrated the capability of PhaseDNN in learning high frequency functions and oscillatory solutions of Helmholtz equations.

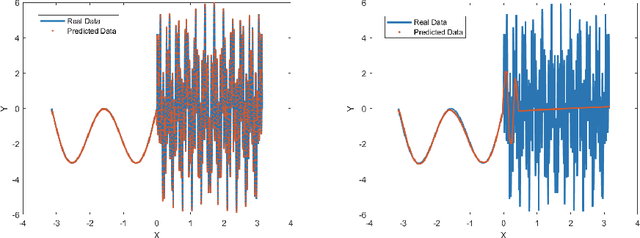
PhaseDNN - A Parallel Phase Shift Deep Neural Network for Adaptive Wideband Learning

In this paper, we propose a phase shift deep neural network (PhaseDNN) which provides a wideband convergence in approximating a high dimensional function during its training of the network. The PhaseDNN utilizes the fact that many DNN achieves convergence in the low frequency range first, thus, a series of moderately-sized of DNNs are constructed and trained in parallel for ranges of higher frequencies. With the help of phase shifts in the frequency domain, implemented through a simple phase factor multiplication on the training data, each DNN in the series will be trained to approximate the target function's higher frequency content over a specific range. Due to the phase shift, each DNN achieves the speed of convergence as in the low frequency range. As a result, the proposed PhaseDNN system is able to convert wideband frequency learning to low frequency learning, thus allowing a uniform learning to wideband high dimensional functions with frequency adaptive training. Numerical results have demonstrated the capability of PhaseDNN in learning information of a target function from low to high frequency uniformly.