A Phase Shift Deep Neural Network for High Frequency Wave Equations in Inhomogeneous Media

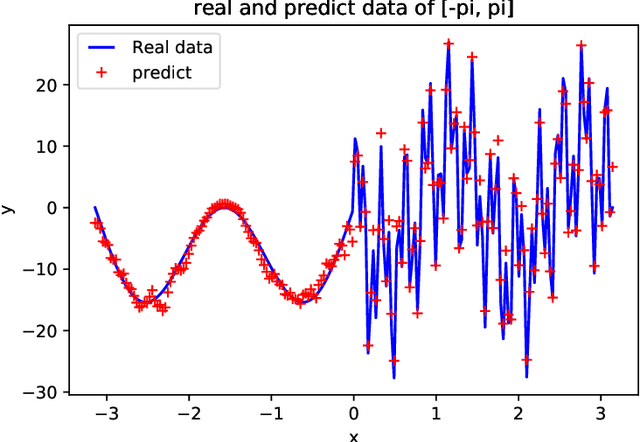
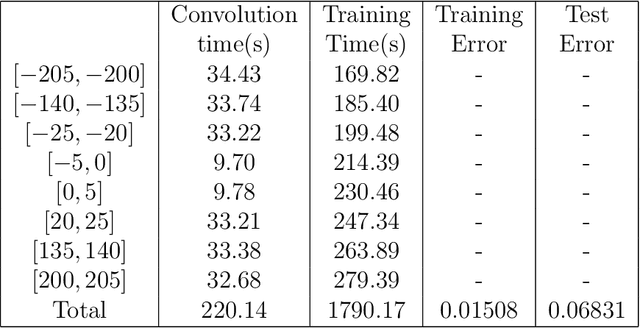
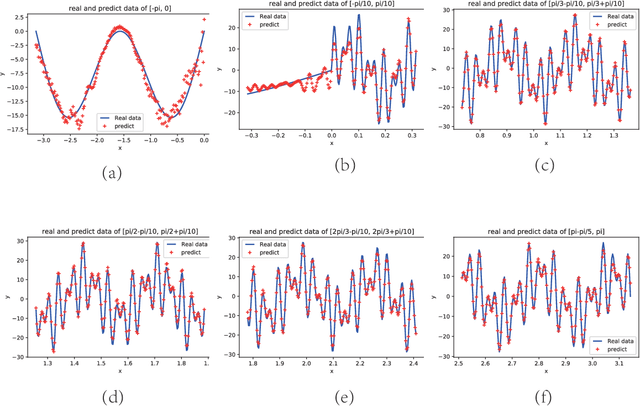
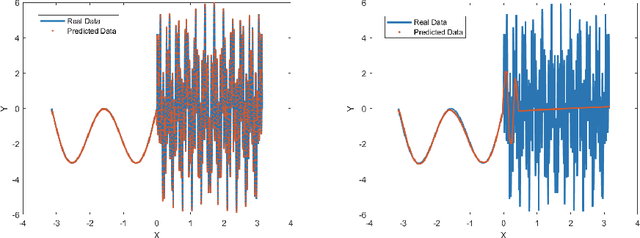
In this paper, we propose a phase shift deep neural network (PhaseDNN) which provides a wideband convergence in approximating high frequency solutions of wave equations. The PhaseDNN accounts for the fact that many DNN achieves convergence in the low frequency range first, a series of moderately-sized of DNNs are constructed and trained for selected high frequency ranges. With the help of phase shifts in the frequency domain, each DNN will be trained to approximate the target solution's higher frequency content over a specific range. Due to the phase shift, each DNN achieves the speed of convergence as in the low frequency range. As a result, the proposed PhaseDNN is able to convert high frequency learning to low frequency learning, thus allowing a uniform learning to wideband high frequency functions. The PhaseDNN will then be applied to find the solution of high frequency wave equations in inhomogeneous media. Numerical results have demonstrated the capability of PhaseDNN in learning high frequency functions and oscillatory solutions of Helmholtz equations.