Robust Fourier Neural Networks

Fourier embedding has shown great promise in removing spectral bias during neural network training. However, it can still suffer from high generalization errors, especially when the labels or measurements are noisy. We demonstrate that introducing a simple diagonal layer after the Fourier embedding layer makes the network more robust to measurement noise, effectively prompting it to learn sparse Fourier features. We provide theoretical justifications for this Fourier feature learning, leveraging recent developments in diagonal networks and implicit regularization in neural networks. Under certain conditions, our proposed approach can also learn functions that are noisy mixtures of nonlinear functions of Fourier features. Numerical experiments validate the effectiveness of our proposed architecture, supporting our theory.

Stochastic approach for elliptic problems in perforated domains

A wide range of applications in science and engineering involve a PDE model in a domain with perforations, such as perforated metals or air filters. Solving such perforated domain problems suffers from computational challenges related to resolving the scale imposed by the geometries of perforations. We propose a neural network-based mesh-free approach for perforated domain problems. The method is robust and efficient in capturing various configuration scales, including the averaged macroscopic behavior of the solution that involves a multiscale nature induced by small perforations. The new approach incorporates the derivative-free loss method that uses a stochastic representation or the Feynman-Kac formulation. In particular, we implement the Neumann boundary condition for the derivative-free loss method to handle the interface between the domain and perforations. A suite of stringent numerical tests is provided to support the proposed method's efficacy in handling various perforation scales.

Learning In-between Imagery Dynamics via Physical Latent Spaces

We present a framework designed to learn the underlying dynamics between two images observed at consecutive time steps. The complex nature of image data and the lack of temporal information pose significant challenges in capturing the unique evolving patterns. Our proposed method focuses on estimating the intermediary stages of image evolution, allowing for interpretability through latent dynamics while preserving spatial correlations with the image. By incorporating a latent variable that follows a physical model expressed in partial differential equations (PDEs), our approach ensures the interpretability of the learned model and provides insight into corresponding image dynamics. We demonstrate the robustness and effectiveness of our learning framework through a series of numerical tests using geoscientific imagery data.

An analysis of the derivative-free loss method for solving PDEs

This study analyzes the derivative-free loss method to solve a certain class of elliptic PDEs using neural networks. The derivative-free loss method uses the Feynman-Kac formulation, incorporating stochastic walkers and their corresponding average values. We investigate the effect of the time interval related to the Feynman-Kac formulation and the walker size in the context of computational efficiency, trainability, and sampling errors. Our analysis shows that the training loss bias is proportional to the time interval and the spatial gradient of the neural network while inversely proportional to the walker size. We also show that the time interval must be sufficiently long to train the network. These analytic results tell that we can choose the walker size as small as possible based on the optimal lower bound of the time interval. We also provide numerical tests supporting our analysis.

A Neural Network Approach for Homogenization of Multiscale Problems

We propose a neural network-based approach to the homogenization of multiscale problems. The proposed method uses a derivative-free formulation of a training loss, which incorporates Brownian walkers to find the macroscopic description of a multiscale PDE solution. Compared with other network-based approaches for multiscale problems, the proposed method is free from the design of hand-crafted neural network architecture and the cell problem to calculate the homogenization coefficient. The exploration neighborhood of the Brownian walkers affects the overall learning trajectory. We determine the bounds of micro- and macro-time steps that capture the local heterogeneous and global homogeneous solution behaviors, respectively, through a neural network. The bounds imply that the computational cost of the proposed method is independent of the microscale periodic structure for the standard periodic problems. We validate the efficiency and robustness of the proposed method through a suite of linear and nonlinear multiscale problems with periodic and random field coefficients.

Hierarchical Learning to Solve Partial Differential Equations Using Physics-Informed Neural Networks

The neural network-based approach to solving partial differential equations has attracted considerable attention due to its simplicity and flexibility in representing the solution of the partial differential equation. In training a neural network, the network learns global features corresponding to low-frequency components while high-frequency components are approximated at a much slower rate. For a class of equations in which the solution contains a wide range of scales, the network training process can suffer from slow convergence and low accuracy due to its inability to capture the high-frequency components. In this work, we propose a hierarchical approach to improve the convergence rate and accuracy of the neural network solution to partial differential equations. The proposed method comprises multi-training levels in which a newly introduced neural network is guided to learn the residual of the previous level approximation. By the nature of neural networks' training process, the high-level correction is inclined to capture the high-frequency components. We validate the efficiency and robustness of the proposed hierarchical approach through a suite of linear and nonlinear partial differential equations.

A Derivative-Free Method for Solving Elliptic Partial Differential Equations with Deep Neural Networks

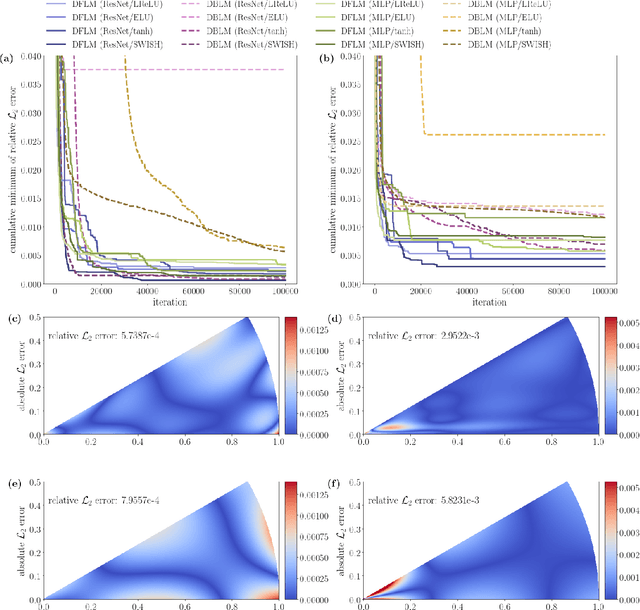
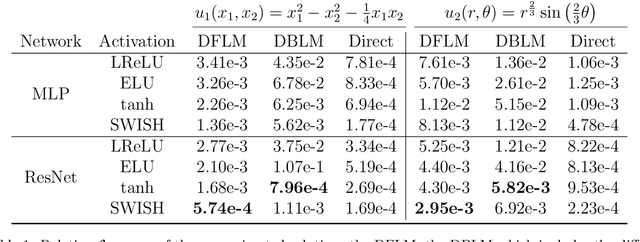
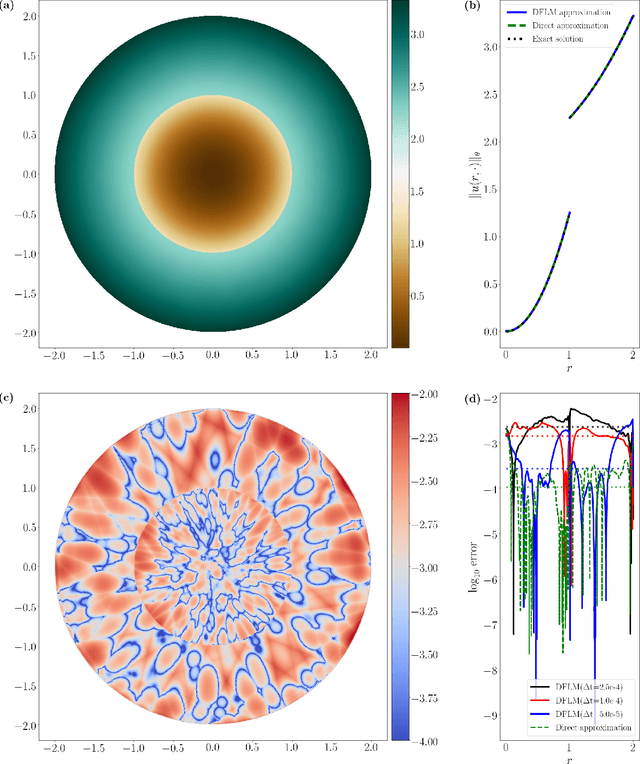
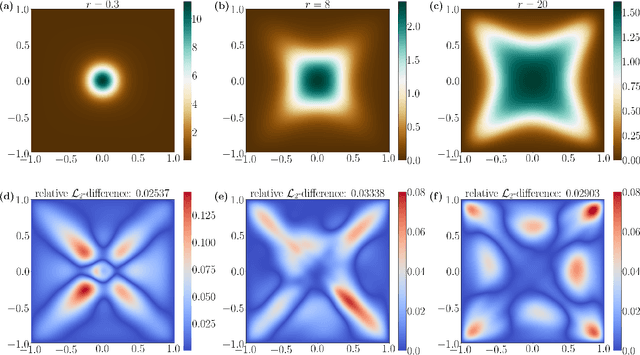
We introduce a deep neural network based method for solving a class of elliptic partial differential equations. We approximate the solution of the PDE with a deep neural network which is trained under the guidance of a probabilistic representation of the PDE in the spirit of the Feynman-Kac formula. The solution is given by an expectation of a martingale process driven by a Brownian motion. As Brownian walkers explore the domain, the deep neural network is iteratively trained using a form of reinforcement learning. Our method is a 'Derivative-Free Loss Method' since it does not require the explicit calculation of the derivatives of the neural network with respect to the input neurons in order to compute the training loss. The advantages of our method are showcased in a series of test problems: a corner singularity problem, an interface problem, and an application to a chemotaxis population model.