Adam R Stinchcombe
A Derivative-Free Method for Solving Elliptic Partial Differential Equations with Deep Neural Networks
Jan 17, 2020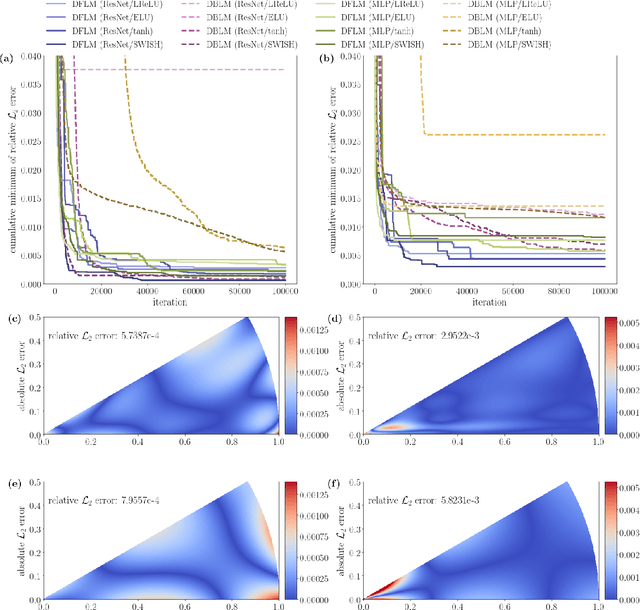
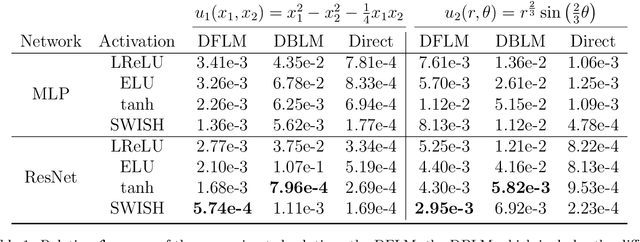
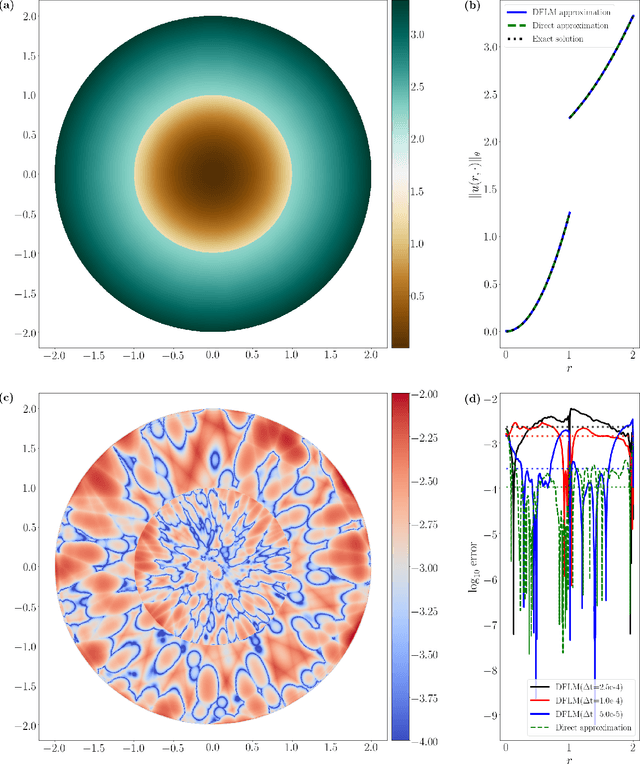
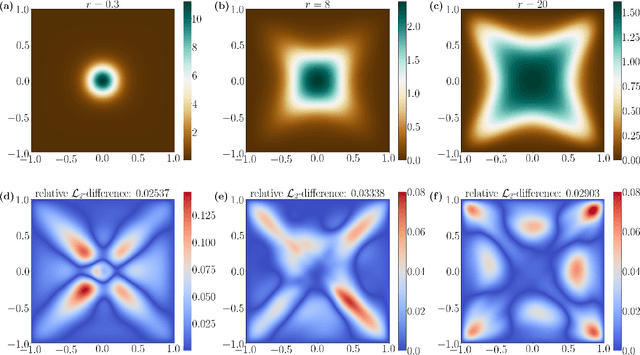
Abstract:We introduce a deep neural network based method for solving a class of elliptic partial differential equations. We approximate the solution of the PDE with a deep neural network which is trained under the guidance of a probabilistic representation of the PDE in the spirit of the Feynman-Kac formula. The solution is given by an expectation of a martingale process driven by a Brownian motion. As Brownian walkers explore the domain, the deep neural network is iteratively trained using a form of reinforcement learning. Our method is a 'Derivative-Free Loss Method' since it does not require the explicit calculation of the derivatives of the neural network with respect to the input neurons in order to compute the training loss. The advantages of our method are showcased in a series of test problems: a corner singularity problem, an interface problem, and an application to a chemotaxis population model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge