Bandit-Driven Batch Selection for Robust Learning under Label Noise

We introduce a novel approach for batch selection in Stochastic Gradient Descent (SGD) training, leveraging combinatorial bandit algorithms. Our methodology focuses on optimizing the learning process in the presence of label noise, a prevalent issue in real-world datasets. Experimental evaluations on the CIFAR-10 dataset reveal that our approach consistently outperforms existing methods across various levels of label corruption. Importantly, we achieve this superior performance without incurring the computational overhead commonly associated with auxiliary neural network models. This work presents a balanced trade-off between computational efficiency and model efficacy, offering a scalable solution for complex machine learning applications.

Differential Equation Scaling Limits of Shaped and Unshaped Neural Networks

Recent analyses of neural networks with shaped activations (i.e. the activation function is scaled as the network size grows) have led to scaling limits described by differential equations. However, these results do not a priori tell us anything about "ordinary" unshaped networks, where the activation is unchanged as the network size grows. In this article, we find similar differential equation based asymptotic characterization for two types of unshaped networks. Firstly, we show that the following two architectures converge to the same infinite-depth-and-width limit at initialization: (i) a fully connected ResNet with a $d^{-1/2}$ factor on the residual branch, where $d$ is the network depth. (ii) a multilayer perceptron (MLP) with depth $d \ll$ width $n$ and shaped ReLU activation at rate $d^{-1/2}$. Secondly, for an unshaped MLP at initialization, we derive the first order asymptotic correction to the layerwise correlation. In particular, if $\rho_\ell$ is the correlation at layer $\ell$, then $q_t = \ell^2 (1 - \rho_\ell)$ with $t = \frac{\ell}{n}$ converges to an SDE with a singularity at $t=0$. These results together provide a connection between shaped and unshaped network architectures, and opens up the possibility of studying the effect of normalization methods and how it connects with shaping activation functions.

Diffusion on the Probability Simplex

Diffusion models learn to reverse the progressive noising of a data distribution to create a generative model. However, the desired continuous nature of the noising process can be at odds with discrete data. To deal with this tension between continuous and discrete objects, we propose a method of performing diffusion on the probability simplex. Using the probability simplex naturally creates an interpretation where points correspond to categorical probability distributions. Our method uses the softmax function applied to an Ornstein-Unlenbeck Process, a well-known stochastic differential equation. We find that our methodology also naturally extends to include diffusion on the unit cube which has applications for bounded image generation.

Network Degeneracy as an Indicator of Training Performance: Comparing Finite and Infinite Width Angle Predictions

Neural networks are powerful functions with widespread use, but the theoretical behaviour of these functions is not fully understood. Creating deep neural networks by stacking many layers has achieved exceptional performance in many applications and contributed to the recent explosion of these methods. Previous works have shown that depth can exponentially increase the expressibility of the network. However, as networks get deeper and deeper, they are more susceptible to becoming degenerate. We observe this degeneracy in the sense that on initialization, inputs tend to become more and more correlated as they travel through the layers of the network. If a network has too many layers, it tends to approximate a (random) constant function, making it effectively incapable of distinguishing between inputs. This seems to affect the training of the network and cause it to perform poorly, as we empirically investigate in this paper. We use a simple algorithm that can accurately predict the level of degeneracy for any given fully connected ReLU network architecture, and demonstrate how the predicted degeneracy relates to training dynamics of the network. We also compare this prediction to predictions derived using infinite width networks.

Dynamic Sparse Training with Structured Sparsity

DST methods achieve state-of-the-art results in sparse neural network training, matching the generalization of dense models while enabling sparse training and inference. Although the resulting models are highly sparse and theoretically cheaper to train, achieving speedups with unstructured sparsity on real-world hardware is challenging. In this work we propose a DST method to learn a variant of structured N:M sparsity, the acceleration of which in general is commonly supported in commodity hardware. Furthermore, we motivate with both a theoretical analysis and empirical results, the generalization performance of our specific N:M sparsity (constant fan-in), present a condensed representation with a reduced parameter and memory footprint, and demonstrate reduced inference time compared to dense models with a naive PyTorch CPU implementation of the condensed representation Our source code is available at https://github.com/calgaryml/condensed-sparsity

Depth Degeneracy in Neural Networks: Vanishing Angles in Fully Connected ReLU Networks on Initialization

Stacking many layers to create truly deep neural networks is arguably what has led to the recent explosion of these methods. However, many properties of deep neural networks are not yet understood. One such mystery is the depth degeneracy phenomenon: the deeper you make your network, the closer your network is to a constant function on initialization. In this paper, we examine the evolution of the angle between two inputs to a ReLU neural network as a function of the number of layers. By using combinatorial expansions, we find precise formulas for how fast this angle goes to zero as depth increases. Our formulas capture microscopic fluctuations that are not visible in the popular framework of infinite width limits, and yet have a significant effect on predicted behaviour. The formulas are given in terms of the mixed moments of correlated Gaussians passed through the ReLU function. We also find a surprising combinatorial connection between these mixed moments and the Bessel numbers.

Bounding generalization error with input compression: An empirical study with infinite-width networks

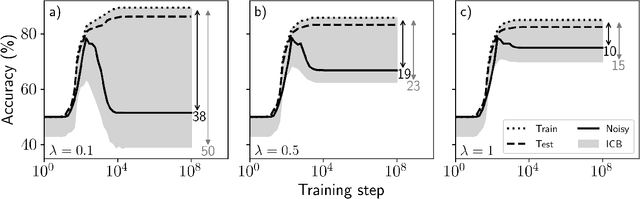
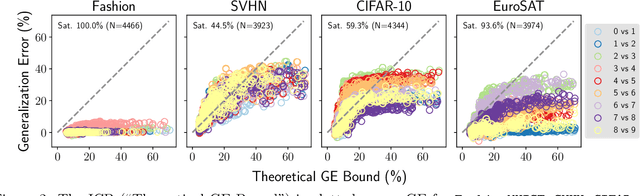
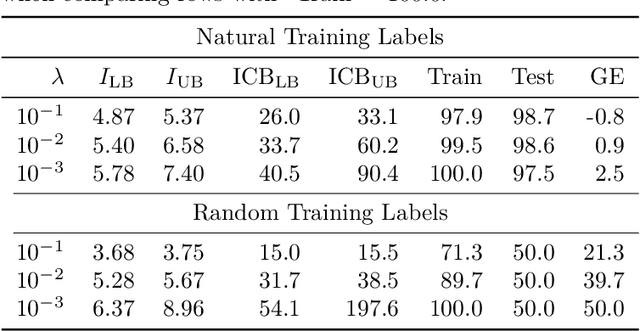
Estimating the Generalization Error (GE) of Deep Neural Networks (DNNs) is an important task that often relies on availability of held-out data. The ability to better predict GE based on a single training set may yield overarching DNN design principles to reduce a reliance on trial-and-error, along with other performance assessment advantages. In search of a quantity relevant to GE, we investigate the Mutual Information (MI) between the input and final layer representations, using the infinite-width DNN limit to bound MI. An existing input compression-based GE bound is used to link MI and GE. To the best of our knowledge, this represents the first empirical study of this bound. In our attempt to empirically falsify the theoretical bound, we find that it is often tight for best-performing models. Furthermore, it detects randomization of training labels in many cases, reflects test-time perturbation robustness, and works well given only few training samples. These results are promising given that input compression is broadly applicable where MI can be estimated with confidence.

The Neural Covariance SDE: Shaped Infinite Depth-and-Width Networks at Initialization

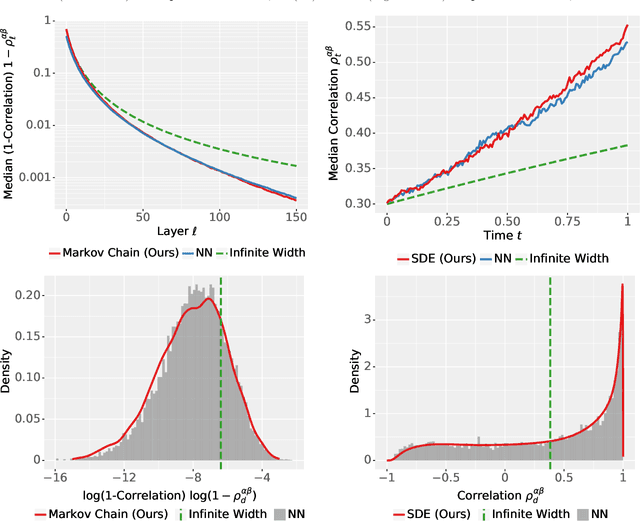
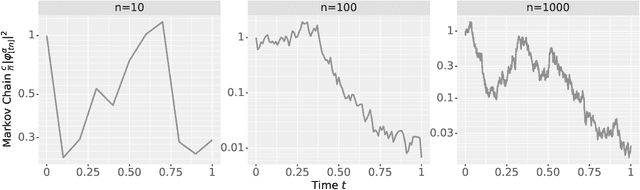
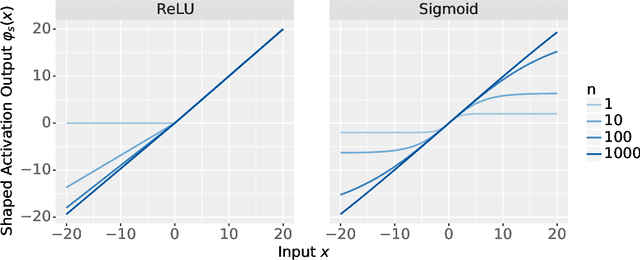
The logit outputs of a feedforward neural network at initialization are conditionally Gaussian, given a random covariance matrix defined by the penultimate layer. In this work, we study the distribution of this random matrix. Recent work has shown that shaping the activation function as network depth grows large is necessary for this covariance matrix to be non-degenerate. However, the current infinite-width-style understanding of this shaping method is unsatisfactory for large depth: infinite-width analyses ignore the microscopic fluctuations from layer to layer, but these fluctuations accumulate over many layers. To overcome this shortcoming, we study the random covariance matrix in the shaped infinite-depth-and-width limit. We identify the precise scaling of the activation function necessary to arrive at a non-trivial limit, and show that the random covariance matrix is governed by a stochastic differential equation (SDE) that we call the Neural Covariance SDE. Using simulations, we show that the SDE closely matches the distribution of the random covariance matrix of finite networks. Additionally, we recover an if-and-only-if condition for exploding and vanishing norms of large shaped networks based on the activation function.

Exponentially Tilted Gaussian Prior for Variational Autoencoder

An important propertyfor deep neural networks to possess is the ability to perform robust out of distribution detection (OOD) on previously unseen data. This property is essential for safety purposes when deploying models for real world applications. Recent studies show that probabilistic generative models can perform poorly on this task, which is surprising given that they seek to estimate the likelihood of training data. To alleviate this issue, we propose the exponentially tilted Gaussian prior distribution for the Variational Autoencoder (VAE). With this prior, we are able to achieve state-of-the art results using just the negative log likelihood that the VAE naturally assigns, while being orders of magnitude faster than some competitive methods. We also show that our model produces high quality image samples which are more crisp than that of a standard Gaussian VAE. The new prior distribution has a very simple implementation which uses a Kullback Leibler divergence that compares the difference between a latent vector's length, and the radius of a sphere.

Finding Critical Scenarios for Automated Driving Systems: A Systematic Literature Review

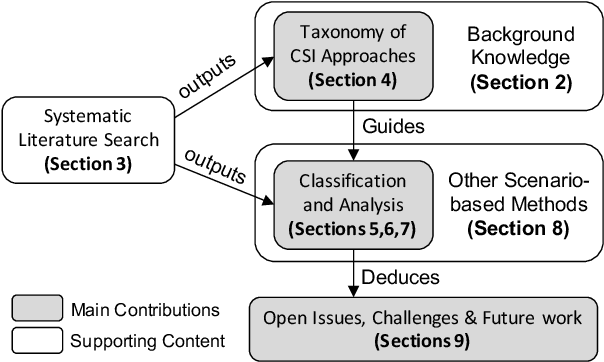
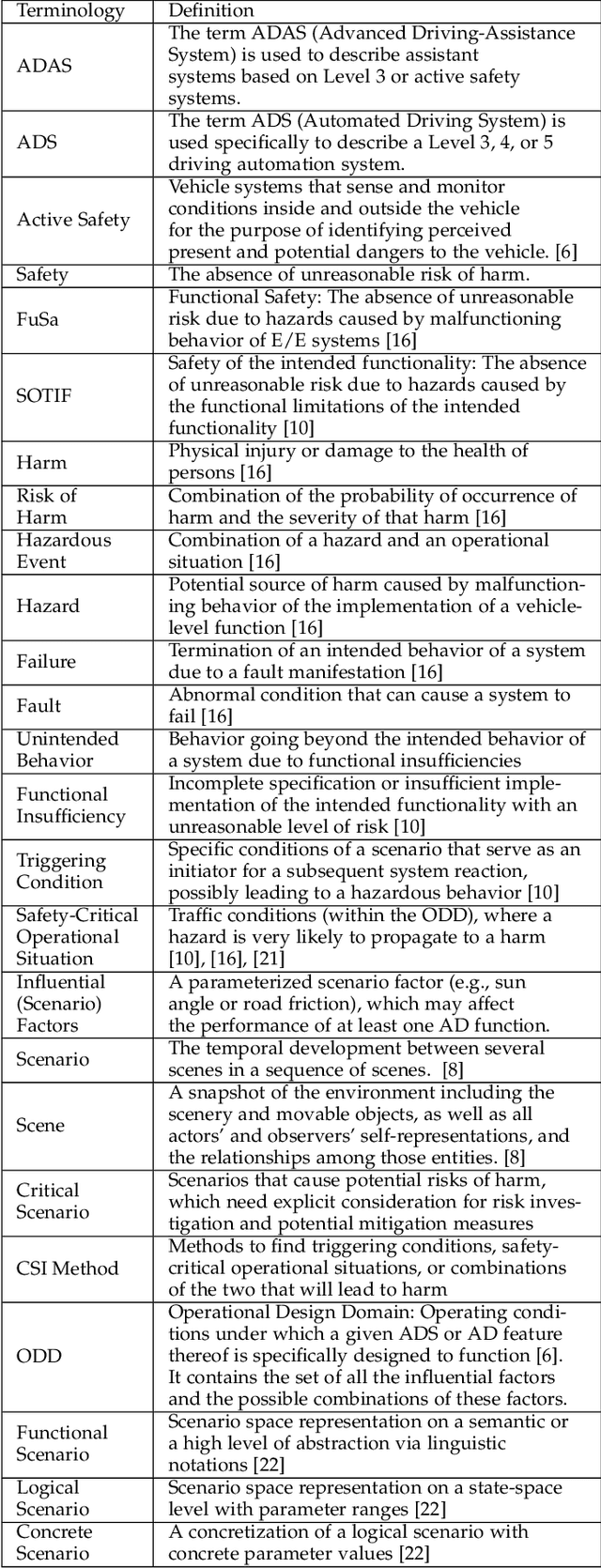
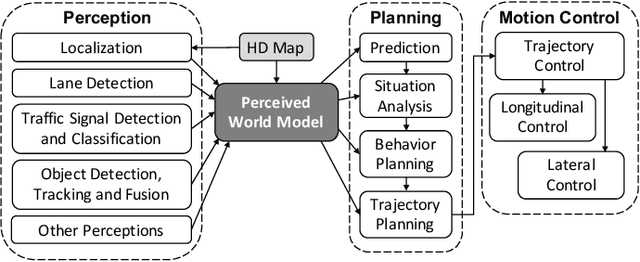
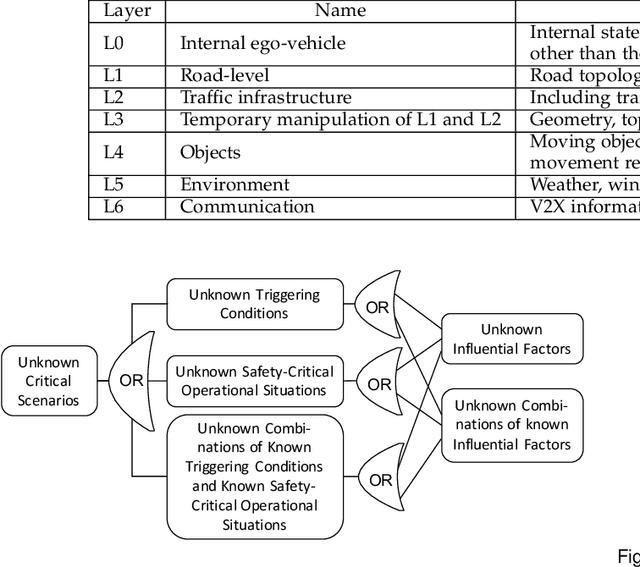
Scenario-based approaches have been receiving a huge amount of attention in research and engineering of automated driving systems. Due to the complexity and uncertainty of the driving environment, and the complexity of the driving task itself, the number of possible driving scenarios that an ADS or ADAS may encounter is virtually infinite. Therefore it is essential to be able to reason about the identification of scenarios and in particular critical ones that may impose unacceptable risk if not considered. Critical scenarios are particularly important to support design, verification and validation efforts, and as a basis for a safety case. In this paper, we present the results of a systematic literature review in the context of autonomous driving. The main contributions are: (i) introducing a comprehensive taxonomy for critical scenario identification methods; (ii) giving an overview of the state-of-the-art research based on the taxonomy encompassing 86 papers between 2017 and 2020; and (iii) identifying open issues and directions for further research. The provided taxonomy comprises three main perspectives encompassing the problem definition (the why), the solution (the methods to derive scenarios), and the assessment of the established scenarios. In addition, we discuss open research issues considering the perspectives of coverage, practicability, and scenario space explosion.