The Zamba2 Suite: Technical Report

In this technical report, we present the Zamba2 series -- a suite of 1.2B, 2.7B, and 7.4B parameter hybrid Mamba2-transformer models that achieve state of the art performance against the leading open-weights models of their class, while achieving substantial gains in inference latency, throughput, and memory efficiency. The Zamba2 series builds upon our initial work with Zamba1-7B, optimizing its architecture, training and annealing datasets, and training for up to three trillion tokens. We provide open-source weights for all models of the Zamba2 series as well as instruction-tuned variants that are strongly competitive against comparable instruct-tuned models of their class. We additionally open-source the pretraining dataset, which we call Zyda-2, used to train the Zamba2 series of models. The models and datasets used in this work are openly available at https://huggingface.co/Zyphra

Dynamic Sparse Training with Structured Sparsity

DST methods achieve state-of-the-art results in sparse neural network training, matching the generalization of dense models while enabling sparse training and inference. Although the resulting models are highly sparse and theoretically cheaper to train, achieving speedups with unstructured sparsity on real-world hardware is challenging. In this work we propose a DST method to learn a variant of structured N:M sparsity, the acceleration of which in general is commonly supported in commodity hardware. Furthermore, we motivate with both a theoretical analysis and empirical results, the generalization performance of our specific N:M sparsity (constant fan-in), present a condensed representation with a reduced parameter and memory footprint, and demonstrate reduced inference time compared to dense models with a naive PyTorch CPU implementation of the condensed representation Our source code is available at https://github.com/calgaryml/condensed-sparsity

Bounding generalization error with input compression: An empirical study with infinite-width networks

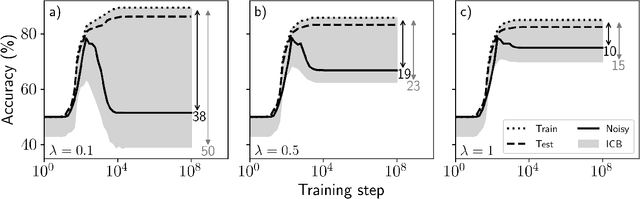
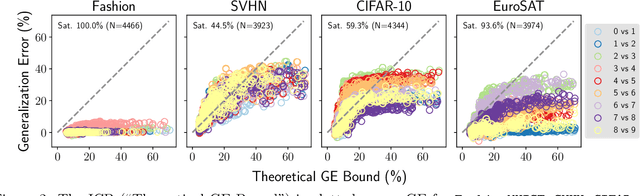
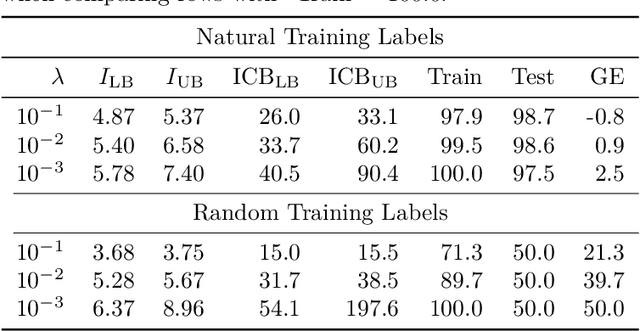
Estimating the Generalization Error (GE) of Deep Neural Networks (DNNs) is an important task that often relies on availability of held-out data. The ability to better predict GE based on a single training set may yield overarching DNN design principles to reduce a reliance on trial-and-error, along with other performance assessment advantages. In search of a quantity relevant to GE, we investigate the Mutual Information (MI) between the input and final layer representations, using the infinite-width DNN limit to bound MI. An existing input compression-based GE bound is used to link MI and GE. To the best of our knowledge, this represents the first empirical study of this bound. In our attempt to empirically falsify the theoretical bound, we find that it is often tight for best-performing models. Furthermore, it detects randomization of training labels in many cases, reflects test-time perturbation robustness, and works well given only few training samples. These results are promising given that input compression is broadly applicable where MI can be estimated with confidence.

Are wider nets better given the same number of parameters?

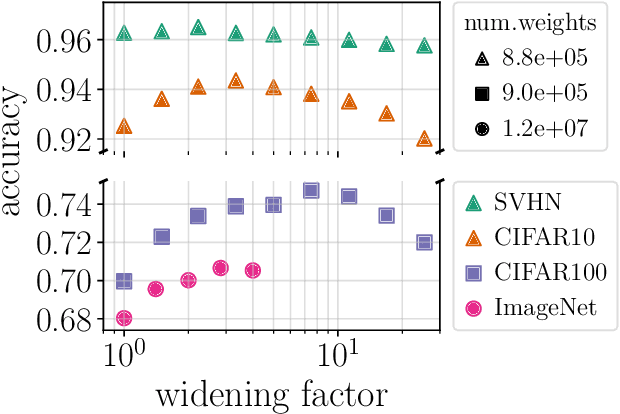
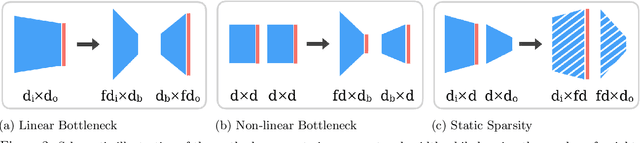
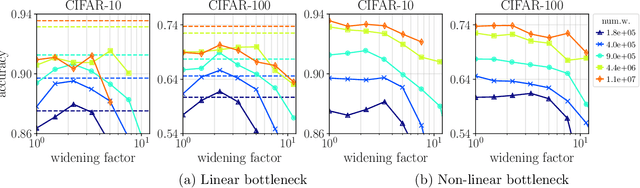
Empirical studies demonstrate that the performance of neural networks improves with increasing number of parameters. In most of these studies, the number of parameters is increased by increasing the network width. This begs the question: Is the observed improvement due to the larger number of parameters, or is it due to the larger width itself? We compare different ways of increasing model width while keeping the number of parameters constant. We show that for models initialized with a random, static sparsity pattern in the weight tensors, network width is the determining factor for good performance, while the number of weights is secondary, as long as trainability is ensured. As a step towards understanding this effect, we analyze these models in the framework of Gaussian Process kernels. We find that the distance between the sparse finite-width model kernel and the infinite-width kernel at initialization is indicative of model performance.

Batch Normalization is a Cause of Adversarial Vulnerability

Batch normalization (batch norm) is often used in an attempt to stabilize and accelerate training in deep neural networks. In many cases it indeed decreases the number of parameter updates required to achieve low training error. However, it also reduces robustness to small adversarial input perturbations and noise by double-digit percentages, as we show on five standard datasets. Furthermore, substituting weight decay for batch norm is sufficient to nullify the relationship between adversarial vulnerability and the input dimension. Our work is consistent with a mean-field analysis that found that batch norm causes exploding gradients.

Adversarial Examples as an Input-Fault Tolerance Problem

We analyze the adversarial examples problem in terms of a model's fault tolerance with respect to its input. Whereas previous work focuses on arbitrarily strict threat models, i.e., $\epsilon$-perturbations, we consider arbitrary valid inputs and propose an information-based characteristic for evaluating tolerance to diverse input faults.