Towards Understanding Inductive Bias in Transformers: A View From Infinity

We study inductive bias in Transformers in the infinitely over-parameterized Gaussian process limit and argue transformers tend to be biased towards more permutation symmetric functions in sequence space. We show that the representation theory of the symmetric group can be used to give quantitative analytical predictions when the dataset is symmetric to permutations between tokens. We present a simplified transformer block and solve the model at the limit, including accurate predictions for the learning curves and network outputs. We show that in common setups, one can derive tight bounds in the form of a scaling law for the learnability as a function of the context length. Finally, we argue WikiText dataset, does indeed possess a degree of permutation symmetry.

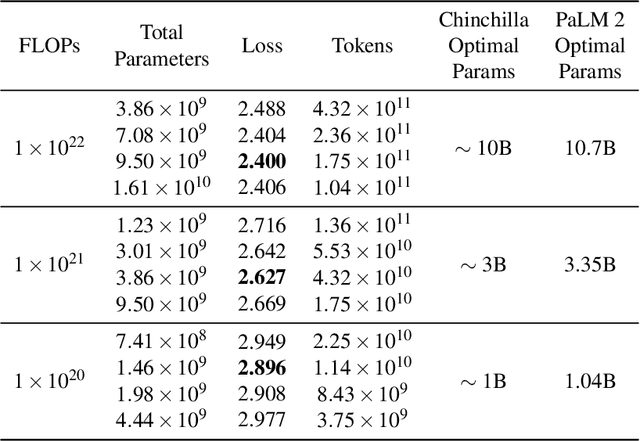
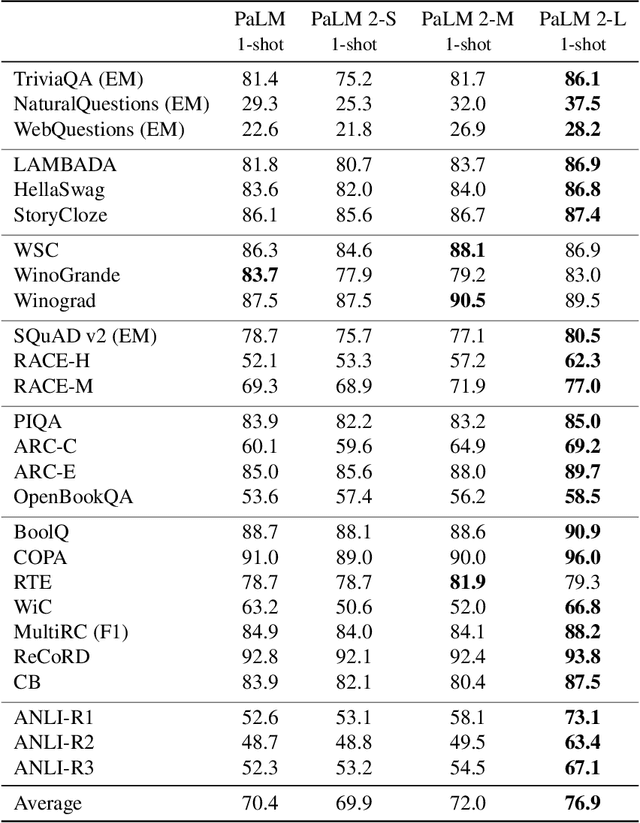
PaLM 2 Technical Report

We introduce PaLM 2, a new state-of-the-art language model that has better multilingual and reasoning capabilities and is more compute-efficient than its predecessor PaLM. PaLM 2 is a Transformer-based model trained using a mixture of objectives. Through extensive evaluations on English and multilingual language, and reasoning tasks, we demonstrate that PaLM 2 has significantly improved quality on downstream tasks across different model sizes, while simultaneously exhibiting faster and more efficient inference compared to PaLM. This improved efficiency enables broader deployment while also allowing the model to respond faster, for a more natural pace of interaction. PaLM 2 demonstrates robust reasoning capabilities exemplified by large improvements over PaLM on BIG-Bench and other reasoning tasks. PaLM 2 exhibits stable performance on a suite of responsible AI evaluations, and enables inference-time control over toxicity without additional overhead or impact on other capabilities. Overall, PaLM 2 achieves state-of-the-art performance across a diverse set of tasks and capabilities. When discussing the PaLM 2 family, it is important to distinguish between pre-trained models (of various sizes), fine-tuned variants of these models, and the user-facing products that use these models. In particular, user-facing products typically include additional pre- and post-processing steps. Additionally, the underlying models may evolve over time. Therefore, one should not expect the performance of user-facing products to exactly match the results reported in this report.

Exploring Length Generalization in Large Language Models

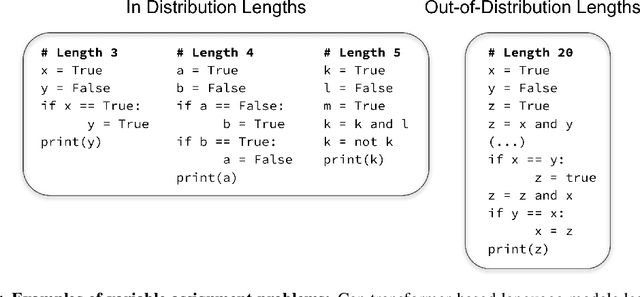
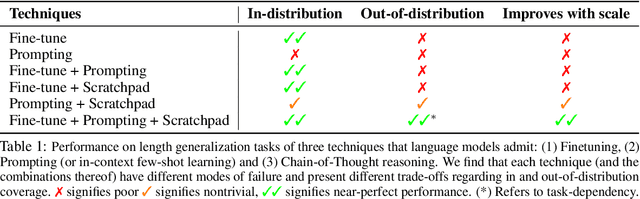
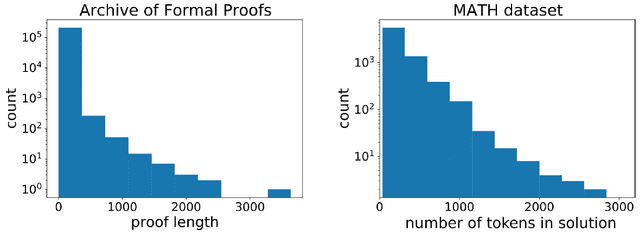
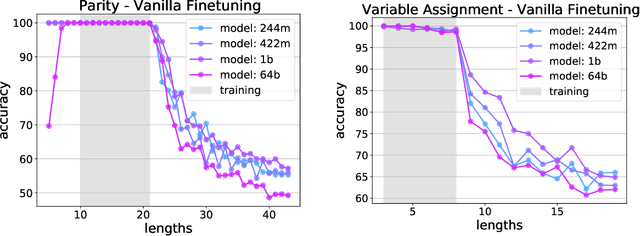
The ability to extrapolate from short problem instances to longer ones is an important form of out-of-distribution generalization in reasoning tasks, and is crucial when learning from datasets where longer problem instances are rare. These include theorem proving, solving quantitative mathematics problems, and reading/summarizing novels. In this paper, we run careful empirical studies exploring the length generalization capabilities of transformer-based language models. We first establish that naively finetuning transformers on length generalization tasks shows significant generalization deficiencies independent of model scale. We then show that combining pretrained large language models' in-context learning abilities with scratchpad prompting (asking the model to output solution steps before producing an answer) results in a dramatic improvement in length generalization. We run careful failure analyses on each of the learning modalities and identify common sources of mistakes that highlight opportunities in equipping language models with the ability to generalize to longer problems.

Solving Quantitative Reasoning Problems with Language Models

Language models have achieved remarkable performance on a wide range of tasks that require natural language understanding. Nevertheless, state-of-the-art models have generally struggled with tasks that require quantitative reasoning, such as solving mathematics, science, and engineering problems at the college level. To help close this gap, we introduce Minerva, a large language model pretrained on general natural language data and further trained on technical content. The model achieves state-of-the-art performance on technical benchmarks without the use of external tools. We also evaluate our model on over two hundred undergraduate-level problems in physics, biology, chemistry, economics, and other sciences that require quantitative reasoning, and find that the model can correctly answer nearly a third of them.

Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models

Language models demonstrate both quantitative improvement and new qualitative capabilities with increasing scale. Despite their potentially transformative impact, these new capabilities are as yet poorly characterized. In order to inform future research, prepare for disruptive new model capabilities, and ameliorate socially harmful effects, it is vital that we understand the present and near-future capabilities and limitations of language models. To address this challenge, we introduce the Beyond the Imitation Game benchmark (BIG-bench). BIG-bench currently consists of 204 tasks, contributed by 442 authors across 132 institutions. Task topics are diverse, drawing problems from linguistics, childhood development, math, common-sense reasoning, biology, physics, social bias, software development, and beyond. BIG-bench focuses on tasks that are believed to be beyond the capabilities of current language models. We evaluate the behavior of OpenAI's GPT models, Google-internal dense transformer architectures, and Switch-style sparse transformers on BIG-bench, across model sizes spanning millions to hundreds of billions of parameters. In addition, a team of human expert raters performed all tasks in order to provide a strong baseline. Findings include: model performance and calibration both improve with scale, but are poor in absolute terms (and when compared with rater performance); performance is remarkably similar across model classes, though with benefits from sparsity; tasks that improve gradually and predictably commonly involve a large knowledge or memorization component, whereas tasks that exhibit "breakthrough" behavior at a critical scale often involve multiple steps or components, or brittle metrics; social bias typically increases with scale in settings with ambiguous context, but this can be improved with prompting.

PaLM: Scaling Language Modeling with Pathways

Large language models have been shown to achieve remarkable performance across a variety of natural language tasks using few-shot learning, which drastically reduces the number of task-specific training examples needed to adapt the model to a particular application. To further our understanding of the impact of scale on few-shot learning, we trained a 540-billion parameter, densely activated, Transformer language model, which we call Pathways Language Model PaLM. We trained PaLM on 6144 TPU v4 chips using Pathways, a new ML system which enables highly efficient training across multiple TPU Pods. We demonstrate continued benefits of scaling by achieving state-of-the-art few-shot learning results on hundreds of language understanding and generation benchmarks. On a number of these tasks, PaLM 540B achieves breakthrough performance, outperforming the finetuned state-of-the-art on a suite of multi-step reasoning tasks, and outperforming average human performance on the recently released BIG-bench benchmark. A significant number of BIG-bench tasks showed discontinuous improvements from model scale, meaning that performance steeply increased as we scaled to our largest model. PaLM also has strong capabilities in multilingual tasks and source code generation, which we demonstrate on a wide array of benchmarks. We additionally provide a comprehensive analysis on bias and toxicity, and study the extent of training data memorization with respect to model scale. Finally, we discuss the ethical considerations related to large language models and discuss potential mitigation strategies.

Show Your Work: Scratchpads for Intermediate Computation with Language Models

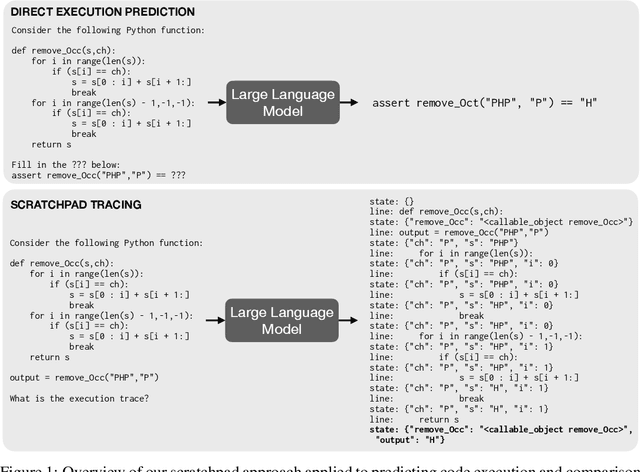
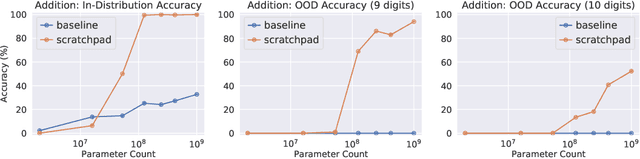
Large pre-trained language models perform remarkably well on tasks that can be done "in one pass", such as generating realistic text or synthesizing computer programs. However, they struggle with tasks that require unbounded multi-step computation, such as adding integers or executing programs. Surprisingly, we find that these same models are able to perform complex multi-step computations -- even in the few-shot regime -- when asked to perform the operation "step by step", showing the results of intermediate computations. In particular, we train transformers to perform multi-step computations by asking them to emit intermediate computation steps into a "scratchpad". On a series of increasingly complex tasks ranging from long addition to the execution of arbitrary programs, we show that scratchpads dramatically improve the ability of language models to perform multi-step computations.

Are wider nets better given the same number of parameters?

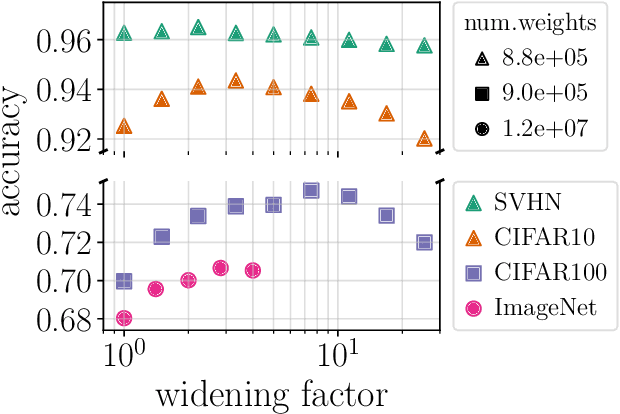
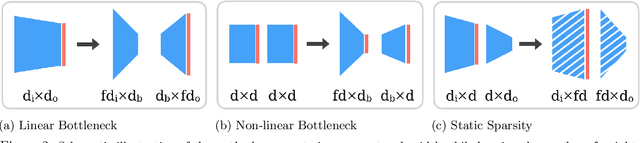
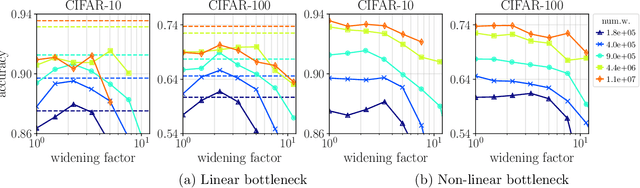
Empirical studies demonstrate that the performance of neural networks improves with increasing number of parameters. In most of these studies, the number of parameters is increased by increasing the network width. This begs the question: Is the observed improvement due to the larger number of parameters, or is it due to the larger width itself? We compare different ways of increasing model width while keeping the number of parameters constant. We show that for models initialized with a random, static sparsity pattern in the weight tensors, network width is the determining factor for good performance, while the number of weights is secondary, as long as trainability is ensured. As a step towards understanding this effect, we analyze these models in the framework of Gaussian Process kernels. We find that the distance between the sparse finite-width model kernel and the infinite-width kernel at initialization is indicative of model performance.

On the training dynamics of deep networks with $L_2$ regularization

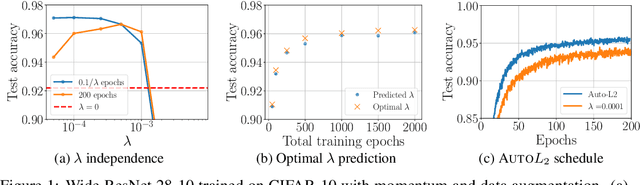
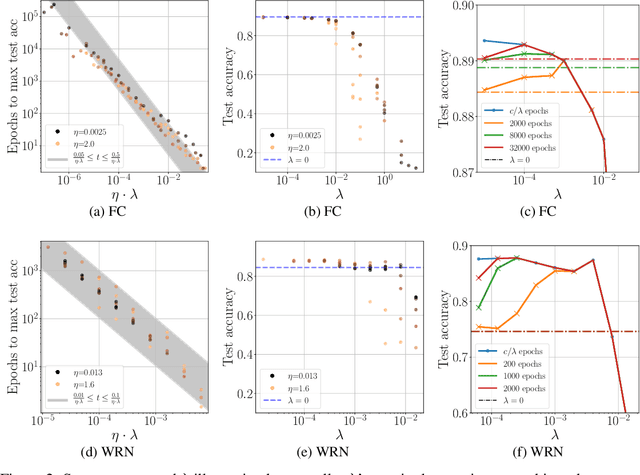
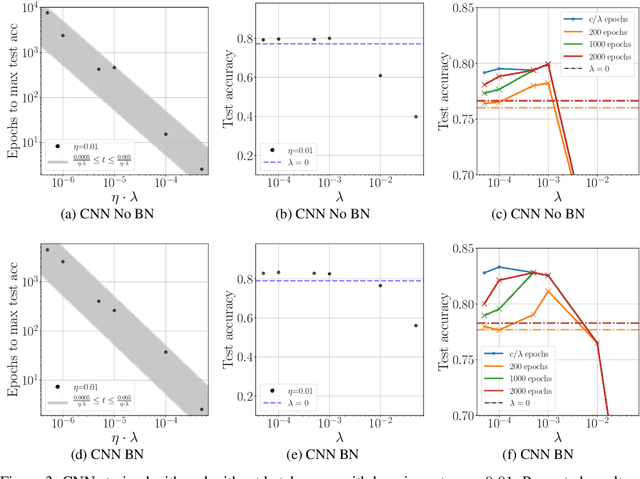
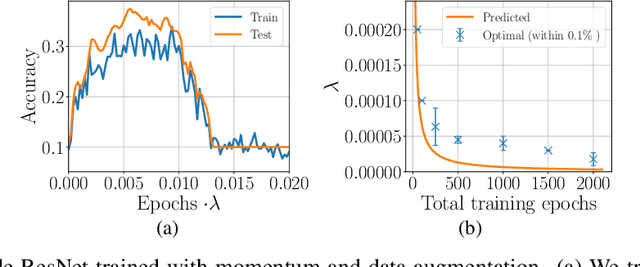
We study the role of $L_2$ regularization in deep learning, and uncover simple relations between the performance of the model, the $L_2$ coefficient, the learning rate, and the number of training steps. These empirical relations hold when the network is overparameterized. They can be used to predict the optimal regularization parameter of a given model. In addition, based on these observations we propose a dynamical schedule for the regularization parameter that improves performance and speeds up training. We test these proposals in modern image classification settings. Finally, we show that these empirical relations can be understood theoretically in the context of infinitely wide networks. We derive the gradient flow dynamics of such networks, and compare the role of $L_2$ regularization in this context with that of linear models.

On the asymptotics of wide networks with polynomial activations

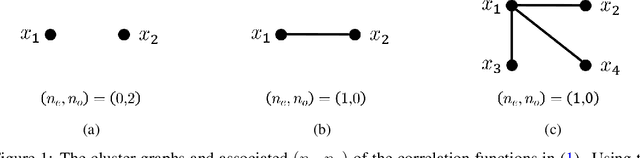
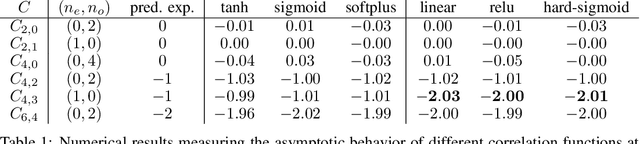
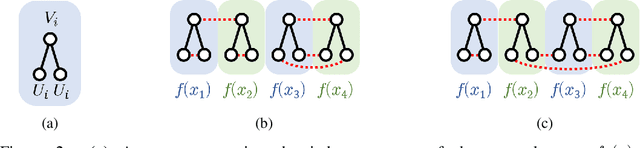
We consider an existing conjecture addressing the asymptotic behavior of neural networks in the large width limit. The results that follow from this conjecture include tight bounds on the behavior of wide networks during stochastic gradient descent, and a derivation of their finite-width dynamics. We prove the conjecture for deep networks with polynomial activation functions, greatly extending the validity of these results. Finally, we point out a difference in the asymptotic behavior of networks with analytic (and non-linear) activation functions and those with piecewise-linear activations such as ReLU.