Zohar Ringel
Applications of Statistical Field Theory in Deep Learning
Feb 25, 2025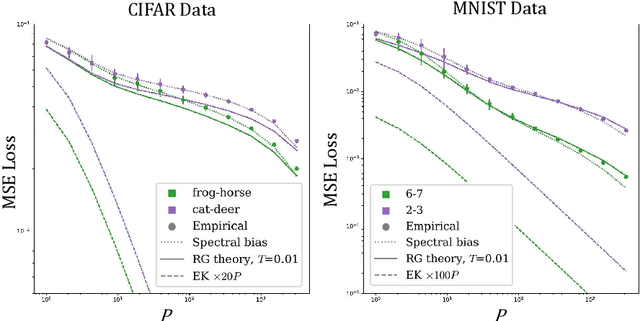
Abstract:Deep learning algorithms have made incredible strides in the past decade yet due to the complexity of these algorithms, the science of deep learning remains in its early stages. Being an experimentally driven field, it is natural to seek a theory of deep learning within the physics paradigm. As deep learning is largely about learning functions and distributions over functions, statistical field theory, a rich and versatile toolbox for tackling complex distributions over functions (fields) is an obvious choice of formalism. Research efforts carried out in the past few years have demonstrated the ability of field theory to provide useful insights on generalization, implicit bias, and feature learning effects. Here we provide a pedagogical review of this emerging line of research.
From Kernels to Features: A Multi-Scale Adaptive Theory of Feature Learning
Feb 05, 2025Abstract:Theoretically describing feature learning in neural networks is crucial for understanding their expressive power and inductive biases, motivating various approaches. Some approaches describe network behavior after training through a simple change in kernel scale from initialization, resulting in a generalization power comparable to a Gaussian process. Conversely, in other approaches training results in the adaptation of the kernel to the data, involving complex directional changes to the kernel. While these approaches capture different facets of network behavior, their relationship and respective strengths across scaling regimes remains an open question. This work presents a theoretical framework of multi-scale adaptive feature learning bridging these approaches. Using methods from statistical mechanics, we derive analytical expressions for network output statistics which are valid across scaling regimes and in the continuum between them. A systematic expansion of the network's probability distribution reveals that mean-field scaling requires only a saddle-point approximation, while standard scaling necessitates additional correction terms. Remarkably, we find across regimes that kernel adaptation can be reduced to an effective kernel rescaling when predicting the mean network output of a linear network. However, even in this case, the multi-scale adaptive approach captures directional feature learning effects, providing richer insights than what could be recovered from a rescaling of the kernel alone.
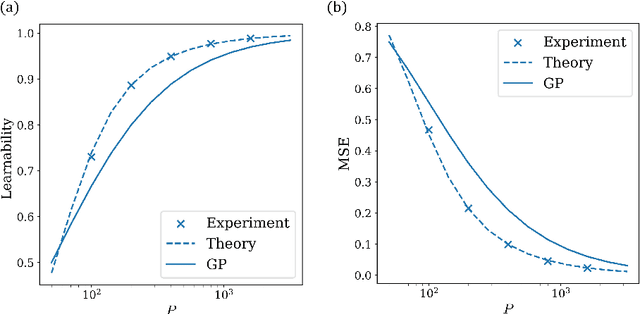
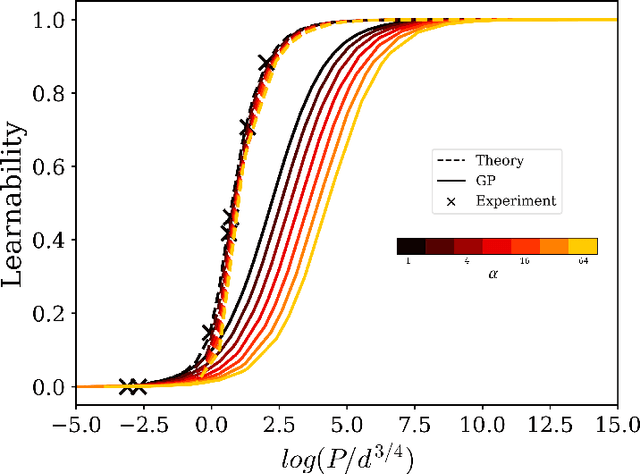
Symmetric Kernels with Non-Symmetric Data: A Data-Agnostic Learnability Bound
Jun 04, 2024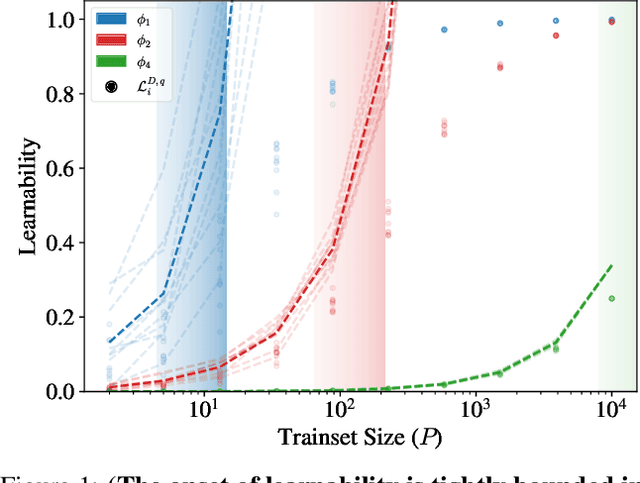
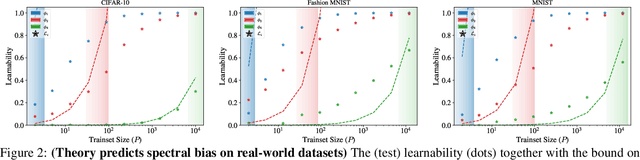
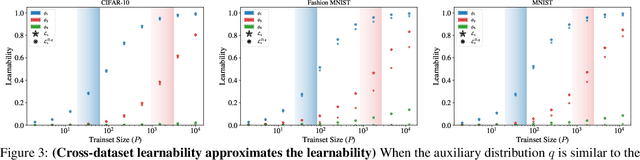
Abstract:Kernel ridge regression (KRR) and Gaussian processes (GPs) are fundamental tools in statistics and machine learning with recent applications to highly over-parameterized deep neural networks. The ability of these tools to learn a target function is directly related to the eigenvalues of their kernel sampled on the input data. Targets having support on higher eigenvalues are more learnable. While kernels are often highly symmetric objects, the data is often not. Thus kernel symmetry seems to have little to no bearing on the above eigenvalues or learnability, making spectral analysis on real-world data challenging. Here, we show that contrary to this common lure, one may use eigenvalues and eigenfunctions associated with highly idealized data-measures to bound learnability on realistic data. As a demonstration, we give a theoretical lower bound on the sample complexity of copying heads for kernels associated with generic transformers acting on natural language.
Wilsonian Renormalization of Neural Network Gaussian Processes
May 09, 2024Abstract:Separating relevant and irrelevant information is key to any modeling process or scientific inquiry. Theoretical physics offers a powerful tool for achieving this in the form of the renormalization group (RG). Here we demonstrate a practical approach to performing Wilsonian RG in the context of Gaussian Process (GP) Regression. We systematically integrate out the unlearnable modes of the GP kernel, thereby obtaining an RG flow of the Gaussian Process in which the data plays the role of the energy scale. In simple cases, this results in a universal flow of the ridge parameter, which becomes input-dependent in the richer scenario in which non-Gaussianities are included. In addition to being analytically tractable, this approach goes beyond structural analogies between RG and neural networks by providing a natural connection between RG flow and learnable vs. unlearnable modes. Studying such flows may improve our understanding of feature learning in deep neural networks, and identify potential universality classes in these models.
Towards Understanding Inductive Bias in Transformers: A View From Infinity
Feb 07, 2024Abstract:We study inductive bias in Transformers in the infinitely over-parameterized Gaussian process limit and argue transformers tend to be biased towards more permutation symmetric functions in sequence space. We show that the representation theory of the symmetric group can be used to give quantitative analytical predictions when the dataset is symmetric to permutations between tokens. We present a simplified transformer block and solve the model at the limit, including accurate predictions for the learning curves and network outputs. We show that in common setups, one can derive tight bounds in the form of a scaling law for the learnability as a function of the context length. Finally, we argue WikiText dataset, does indeed possess a degree of permutation symmetry.
Droplets of Good Representations: Grokking as a First Order Phase Transition in Two Layer Networks
Oct 05, 2023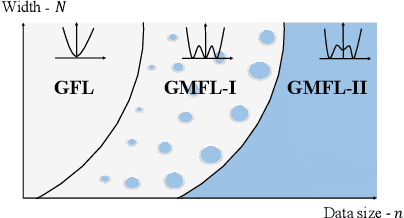

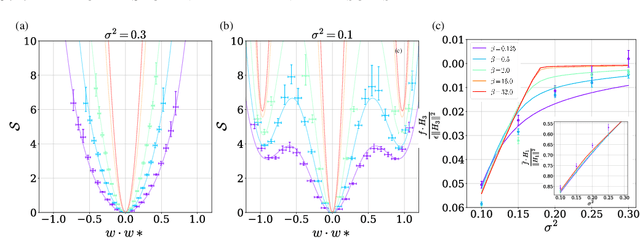
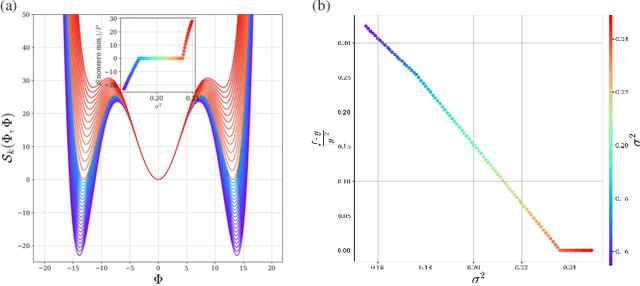
Abstract:A key property of deep neural networks (DNNs) is their ability to learn new features during training. This intriguing aspect of deep learning stands out most clearly in recently reported Grokking phenomena. While mainly reflected as a sudden increase in test accuracy, Grokking is also believed to be a beyond lazy-learning/Gaussian Process (GP) phenomenon involving feature learning. Here we apply a recent development in the theory of feature learning, the adaptive kernel approach, to two teacher-student models with cubic-polynomial and modular addition teachers. We provide analytical predictions on feature learning and Grokking properties of these models and demonstrate a mapping between Grokking and the theory of phase transitions. We show that after Grokking, the state of the DNN is analogous to the mixed phase following a first-order phase transition. In this mixed phase, the DNN generates useful internal representations of the teacher that are sharply distinct from those before the transition.
Speed Limits for Deep Learning
Jul 27, 2023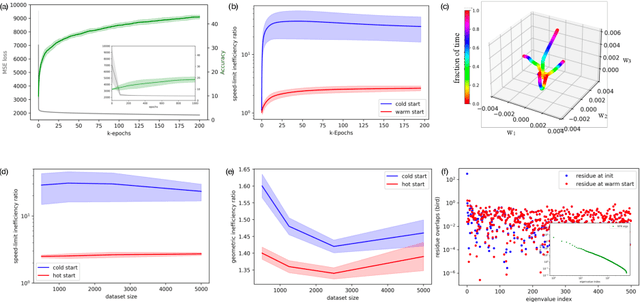
Abstract:State-of-the-art neural networks require extreme computational power to train. It is therefore natural to wonder whether they are optimally trained. Here we apply a recent advancement in stochastic thermodynamics which allows bounding the speed at which one can go from the initial weight distribution to the final distribution of the fully trained network, based on the ratio of their Wasserstein-2 distance and the entropy production rate of the dynamical process connecting them. Considering both gradient-flow and Langevin training dynamics, we provide analytical expressions for these speed limits for linear and linearizable neural networks e.g. Neural Tangent Kernel (NTK). Remarkably, given some plausible scaling assumptions on the NTK spectra and spectral decomposition of the labels -- learning is optimal in a scaling sense. Our results are consistent with small-scale experiments with Convolutional Neural Networks (CNNs) and Fully Connected Neural networks (FCNs) on CIFAR-10, showing a short highly non-optimal regime followed by a longer optimal regime.
Spectral-Bias and Kernel-Task Alignment in Physically Informed Neural Networks
Jul 12, 2023Abstract:Physically informed neural networks (PINNs) are a promising emerging method for solving differential equations. As in many other deep learning approaches, the choice of PINN design and training protocol requires careful craftsmanship. Here, we suggest a comprehensive theoretical framework that sheds light on this important problem. Leveraging an equivalence between infinitely over-parameterized neural networks and Gaussian process regression (GPR), we derive an integro-differential equation that governs PINN prediction in the large data-set limit -- the Neurally-Informed Equation (NIE). This equation augments the original one by a kernel term reflecting architecture choices and allows quantifying implicit bias induced by the network via a spectral decomposition of the source term in the original differential equation.
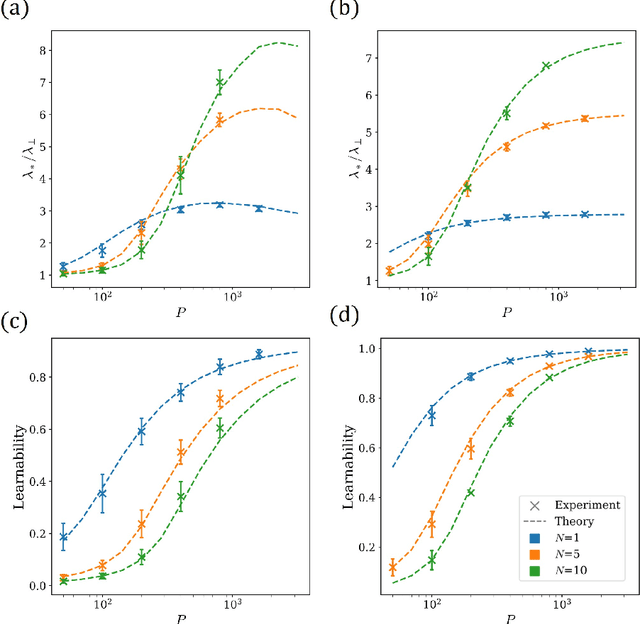
Separation of scales and a thermodynamic description of feature learning in some CNNs
Dec 31, 2021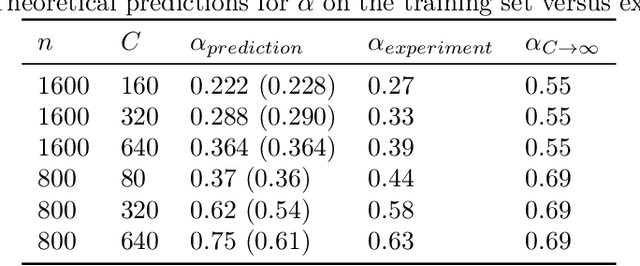
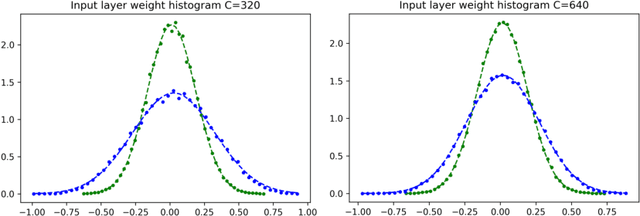
Abstract:Deep neural networks (DNNs) are powerful tools for compressing and distilling information. Due to their scale and complexity, often involving billions of inter-dependent internal degrees of freedom, exact analysis approaches often fall short. A common strategy in such cases is to identify slow degrees of freedom that average out the erratic behavior of the underlying fast microscopic variables. Here, we identify such a separation of scales occurring in over-parameterized deep convolutional neural networks (CNNs) at the end of training. It implies that neuron pre-activations fluctuate in a nearly Gaussian manner with a deterministic latent kernel. While for CNNs with infinitely many channels these kernels are inert, for finite CNNs they adapt and learn from data in an analytically tractable manner. The resulting thermodynamic theory of deep learning yields accurate predictions on several deep non-linear CNN toy models. In addition, it provides new ways of analyzing and understanding CNNs.
A self consistent theory of Gaussian Processes captures feature learning effects in finite CNNs
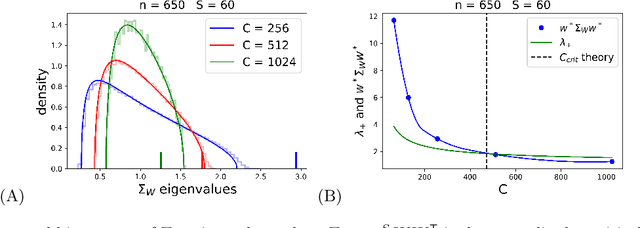
Jun 08, 2021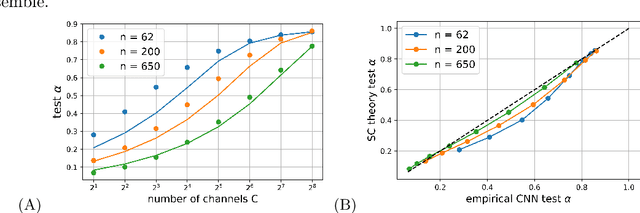
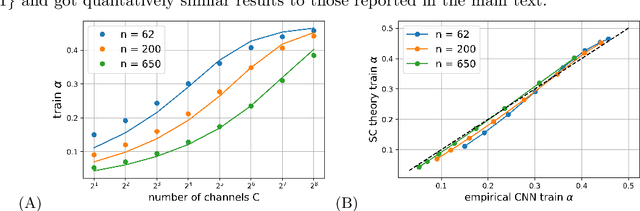
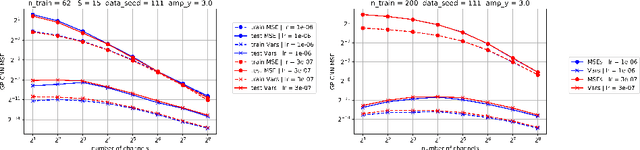
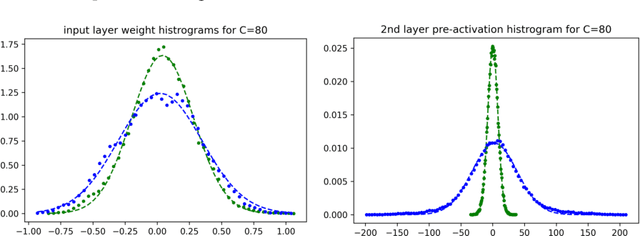
Abstract:Deep neural networks (DNNs) in the infinite width/channel limit have received much attention recently, as they provide a clear analytical window to deep learning via mappings to Gaussian Processes (GPs). Despite its theoretical appeal, this viewpoint lacks a crucial ingredient of deep learning in finite DNNs, laying at the heart of their success -- feature learning. Here we consider DNNs trained with noisy gradient descent on a large training set and derive a self consistent Gaussian Process theory accounting for strong finite-DNN and feature learning effects. Applying this to a toy model of a two-layer linear convolutional neural network (CNN) shows good agreement with experiments. We further identify, both analytical and numerically, a sharp transition between a feature learning regime and a lazy learning regime in this model. Strong finite-DNN effects are also derived for a non-linear two-layer fully connected network. Our self consistent theory provides a rich and versatile analytical framework for studying feature learning and other non-lazy effects in finite DNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge