How to pick the best anomaly detector?

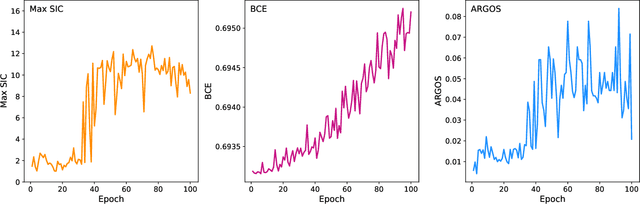
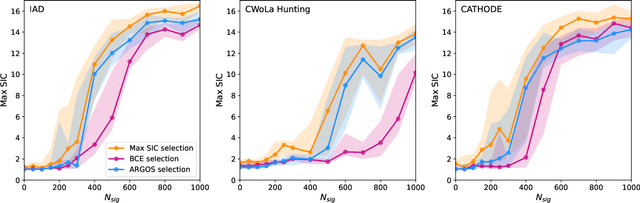
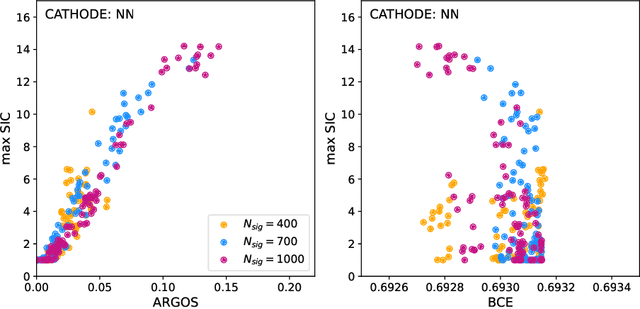
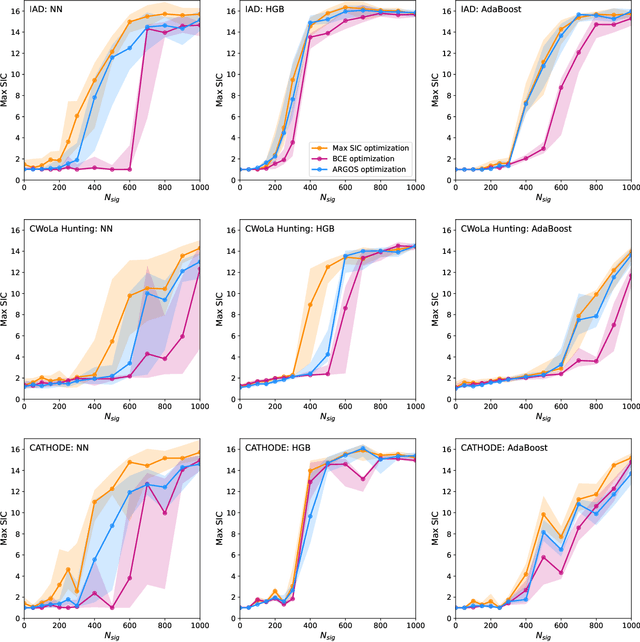
Anomaly detection has the potential to discover new physics in unexplored regions of the data. However, choosing the best anomaly detector for a given data set in a model-agnostic way is an important challenge which has hitherto largely been neglected. In this paper, we introduce the data-driven ARGOS metric, which has a sound theoretical foundation and is empirically shown to robustly select the most sensitive anomaly detection model given the data. Focusing on weakly-supervised, classifier-based anomaly detection methods, we show that the ARGOS metric outperforms other model selection metrics previously used in the literature, in particular the binary cross-entropy loss. We explore several realistic applications, including hyperparameter tuning as well as architecture and feature selection, and in all cases we demonstrate that ARGOS is robust to the noisy conditions of anomaly detection.

Agents of Discovery

The substantial data volumes encountered in modern particle physics and other domains of fundamental physics research allow (and require) the use of increasingly complex data analysis tools and workflows. While the use of machine learning (ML) tools for data analysis has recently proliferated, these tools are typically special-purpose algorithms that rely, for example, on encoded physics knowledge to reach optimal performance. In this work, we investigate a new and orthogonal direction: Using recent progress in large language models (LLMs) to create a team of agents -- instances of LLMs with specific subtasks -- that jointly solve data analysis-based research problems in a way similar to how a human researcher might: by creating code to operate standard tools and libraries (including ML systems) and by building on results of previous iterations. If successful, such agent-based systems could be deployed to automate routine analysis components to counteract the increasing complexity of modern tool chains. To investigate the capabilities of current-generation commercial LLMs, we consider the task of anomaly detection via the publicly available and highly-studied LHC Olympics dataset. Several current models by OpenAI (GPT-4o, o4-mini, GPT-4.1, and GPT-5) are investigated and their stability tested. Overall, we observe the capacity of the agent-based system to solve this data analysis problem. The best agent-created solutions mirror the performance of human state-of-the-art results.

From Kernels to Features: A Multi-Scale Adaptive Theory of Feature Learning

Theoretically describing feature learning in neural networks is crucial for understanding their expressive power and inductive biases, motivating various approaches. Some approaches describe network behavior after training through a simple change in kernel scale from initialization, resulting in a generalization power comparable to a Gaussian process. Conversely, in other approaches training results in the adaptation of the kernel to the data, involving complex directional changes to the kernel. While these approaches capture different facets of network behavior, their relationship and respective strengths across scaling regimes remains an open question. This work presents a theoretical framework of multi-scale adaptive feature learning bridging these approaches. Using methods from statistical mechanics, we derive analytical expressions for network output statistics which are valid across scaling regimes and in the continuum between them. A systematic expansion of the network's probability distribution reveals that mean-field scaling requires only a saddle-point approximation, while standard scaling necessitates additional correction terms. Remarkably, we find across regimes that kernel adaptation can be reduced to an effective kernel rescaling when predicting the mean network output of a linear network. However, even in this case, the multi-scale adaptive approach captures directional feature learning effects, providing richer insights than what could be recovered from a rescaling of the kernel alone.

Large Physics Models: Towards a collaborative approach with Large Language Models and Foundation Models

This paper explores ideas and provides a potential roadmap for the development and evaluation of physics-specific large-scale AI models, which we call Large Physics Models (LPMs). These models, based on foundation models such as Large Language Models (LLMs) - trained on broad data - are tailored to address the demands of physics research. LPMs can function independently or as part of an integrated framework. This framework can incorporate specialized tools, including symbolic reasoning modules for mathematical manipulations, frameworks to analyse specific experimental and simulated data, and mechanisms for synthesizing theories and scientific literature. We begin by examining whether the physics community should actively develop and refine dedicated models, rather than relying solely on commercial LLMs. We then outline how LPMs can be realized through interdisciplinary collaboration among experts in physics, computer science, and philosophy of science. To integrate these models effectively, we identify three key pillars: Development, Evaluation, and Philosophical Reflection. Development focuses on constructing models capable of processing physics texts, mathematical formulations, and diverse physical data. Evaluation assesses accuracy and reliability by testing and benchmarking. Finally, Philosophical Reflection encompasses the analysis of broader implications of LLMs in physics, including their potential to generate new scientific understanding and what novel collaboration dynamics might arise in research. Inspired by the organizational structure of experimental collaborations in particle physics, we propose a similarly interdisciplinary and collaborative approach to building and refining Large Physics Models. This roadmap provides specific objectives, defines pathways to achieve them, and identifies challenges that must be addressed to realise physics-specific large scale AI models.

Aspen Open Jets: Unlocking LHC Data for Foundation Models in Particle Physics

Foundation models are deep learning models pre-trained on large amounts of data which are capable of generalizing to multiple datasets and/or downstream tasks. This work demonstrates how data collected by the CMS experiment at the Large Hadron Collider can be useful in pre-training foundation models for HEP. Specifically, we introduce the AspenOpenJets dataset, consisting of approximately 180M high $p_T$ jets derived from CMS 2016 Open Data. We show how pre-training the OmniJet-$\alpha$ foundation model on AspenOpenJets improves performance on generative tasks with significant domain shift: generating boosted top and QCD jets from the simulated JetClass dataset. In addition to demonstrating the power of pre-training of a jet-based foundation model on actual proton-proton collision data, we provide the ML-ready derived AspenOpenJets dataset for further public use.

A theory of data variability in Neural Network Bayesian inference

Bayesian inference and kernel methods are well established in machine learning. The neural network Gaussian process in particular provides a concept to investigate neural networks in the limit of infinitely wide hidden layers by using kernel and inference methods. Here we build upon this limit and provide a field-theoretic formalism which covers the generalization properties of infinitely wide networks. We systematically compute generalization properties of linear, non-linear, and deep non-linear networks for kernel matrices with heterogeneous entries. In contrast to currently employed spectral methods we derive the generalization properties from the statistical properties of the input, elucidating the interplay of input dimensionality, size of the training data set, and variability of the data. We show that data variability leads to a non-Gaussian action reminiscent of a ($\varphi^3+\varphi^4$)-theory. Using our formalism on a synthetic task and on MNIST we obtain a homogeneous kernel matrix approximation for the learning curve as well as corrections due to data variability which allow the estimation of the generalization properties and exact results for the bounds of the learning curves in the case of infinitely many training data points.

Unified Field Theory for Deep and Recurrent Neural Networks

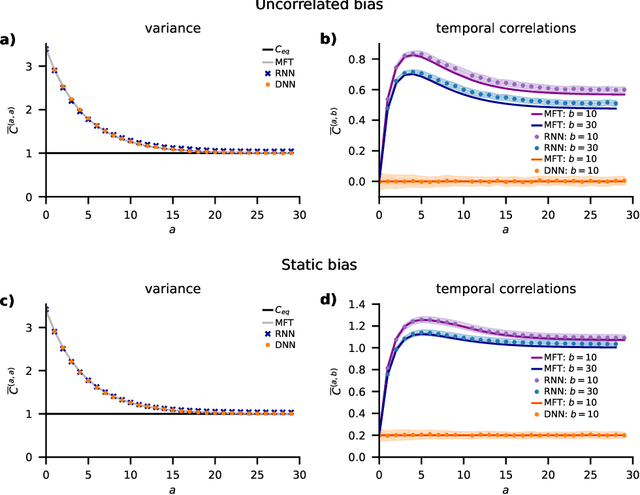
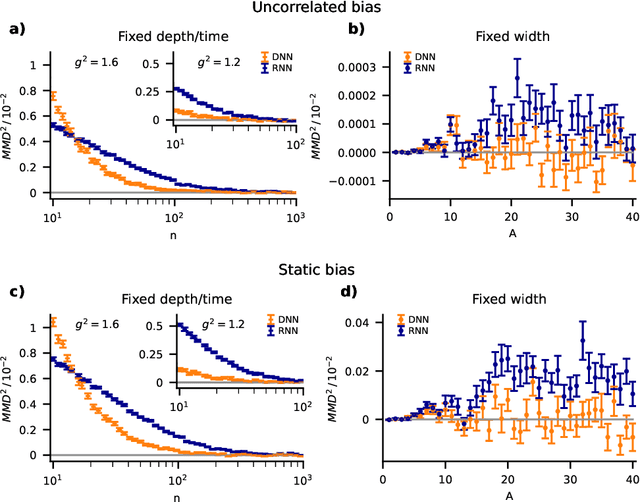
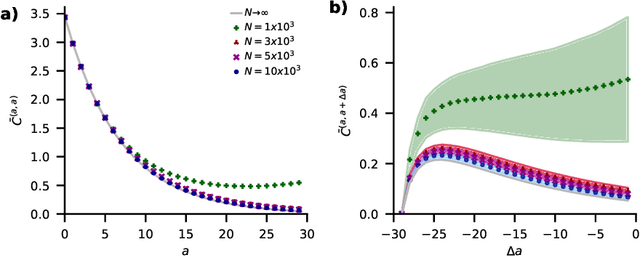
Understanding capabilities and limitations of different network architectures is of fundamental importance to machine learning. Bayesian inference on Gaussian processes has proven to be a viable approach for studying recurrent and deep networks in the limit of infinite layer width, $n\to\infty$. Here we present a unified and systematic derivation of the mean-field theory for both architectures that starts from first principles by employing established methods from statistical physics of disordered systems. The theory elucidates that while the mean-field equations are different with regard to their temporal structure, they yet yield identical Gaussian kernels when readouts are taken at a single time point or layer, respectively. Bayesian inference applied to classification then predicts identical performance and capabilities for the two architectures. Numerically, we find that convergence towards the mean-field theory is typically slower for recurrent networks than for deep networks and the convergence speed depends non-trivially on the parameters of the weight prior as well as the depth or number of time steps, respectively. Our method exposes that Gaussian processes are but the lowest order of a systematic expansion in $1/n$. The formalism thus paves the way to investigate the fundamental differences between recurrent and deep architectures at finite widths $n$.

Constraining dark matter annihilation with cosmic ray antiprotons using neural networks

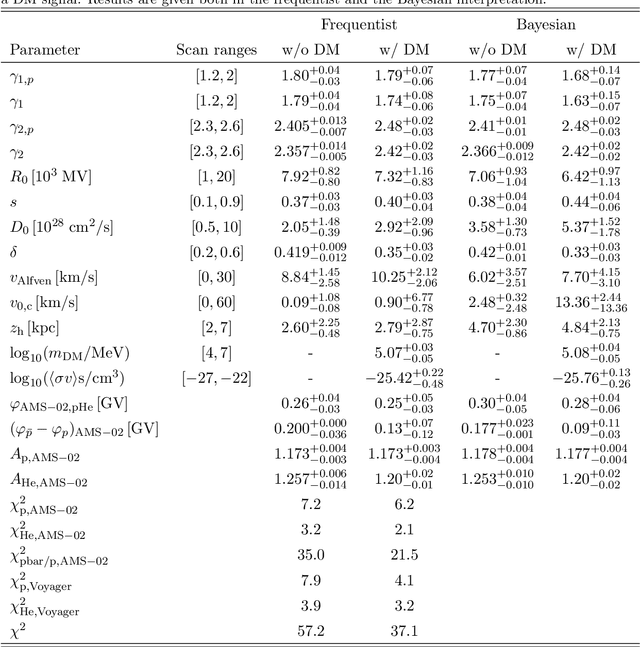
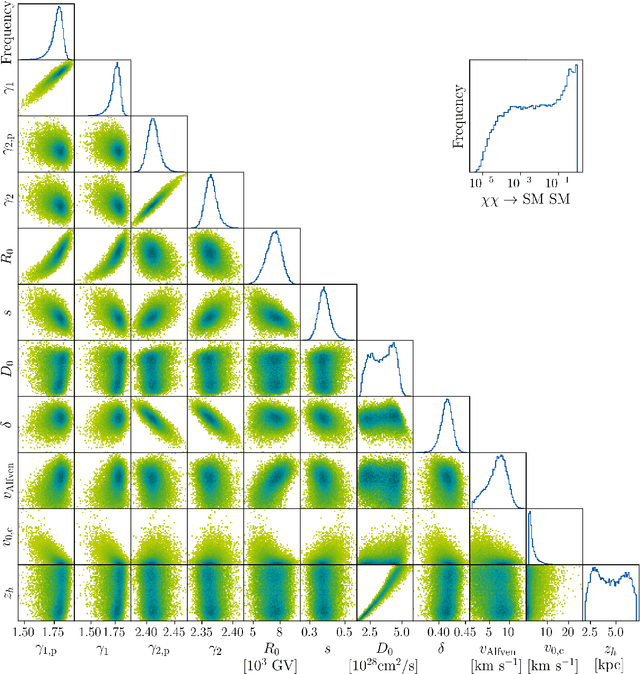
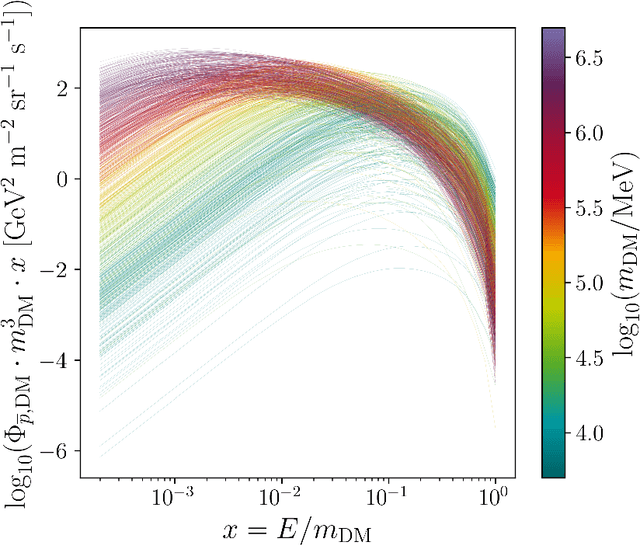
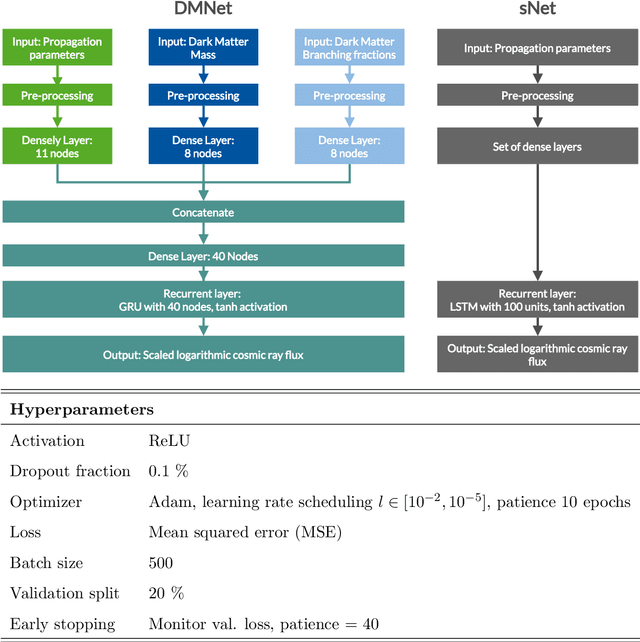
The interpretation of data from indirect detection experiments searching for dark matter annihilations requires computationally expensive simulations of cosmic-ray propagation. In this work we present a new method based on Recurrent Neural Networks that significantly accelerates simulations of secondary and dark matter Galactic cosmic ray antiprotons while achieving excellent accuracy. This approach allows for an efficient profiling or marginalisation over the nuisance parameters of a cosmic ray propagation model in order to perform parameter scans for a wide range of dark matter models. We identify importance sampling as particularly suitable for ensuring that the network is only evaluated in well-trained parameter regions. We present resulting constraints using the most recent AMS-02 antiproton data on several models of Weakly Interacting Massive Particles. The fully trained networks are released as DarkRayNet together with this work and achieve a speed-up of the runtime by at least two orders of magnitude compared to conventional approaches.

Autoencoders for unsupervised anomaly detection in high energy physics

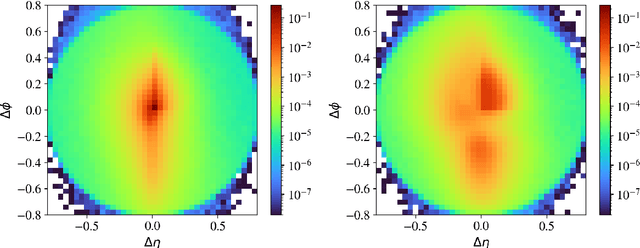
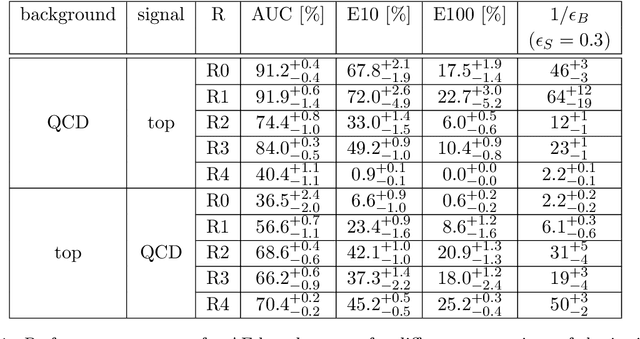
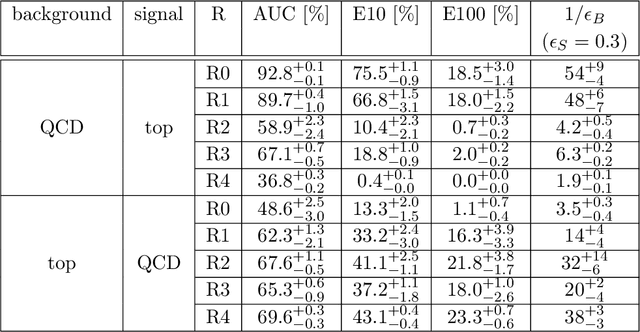
Autoencoders are widely used in machine learning applications, in particular for anomaly detection. Hence, they have been introduced in high energy physics as a promising tool for model-independent new physics searches. We scrutinize the usage of autoencoders for unsupervised anomaly detection based on reconstruction loss to show their capabilities, but also their limitations. As a particle physics benchmark scenario, we study the tagging of top jet images in a background of QCD jet images. Although we reproduce the positive results from the literature, we show that the standard autoencoder setup cannot be considered as a model-independent anomaly tagger by inverting the task: due to the sparsity and the specific structure of the jet images, the autoencoder fails to tag QCD jets if it is trained on top jets even in a semi-supervised setup. Since the same autoencoder architecture can be a good tagger for a specific example of an anomaly and a bad tagger for a different example, we suggest improved performance measures for the task of model-independent anomaly detection. We also improve the capability of the autoencoder to learn non-trivial features of the jet images, such that it is able to achieve both top jet tagging and the inverse task of QCD jet tagging with the same setup. However, we want to stress that a truly model-independent and powerful autoencoder-based unsupervised jet tagger still needs to be developed.