CaloChallenge 2022: A Community Challenge for Fast Calorimeter Simulation

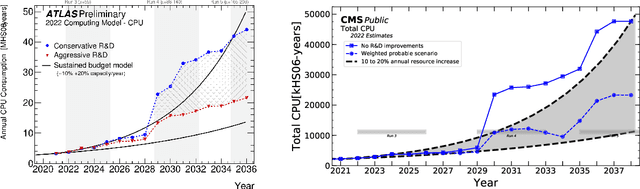
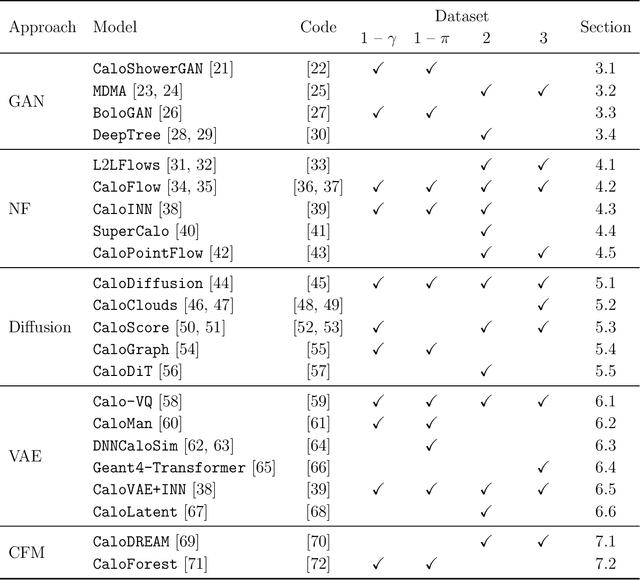
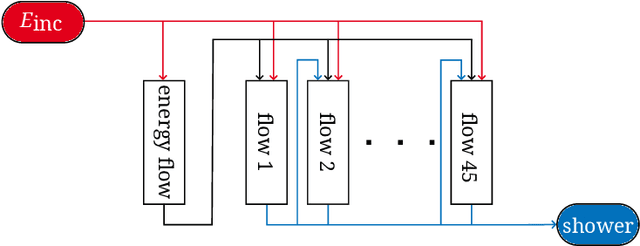
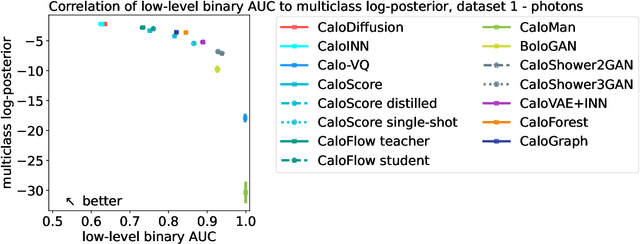
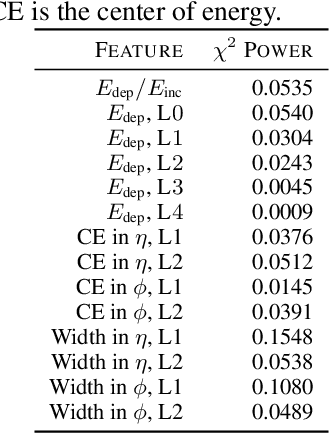
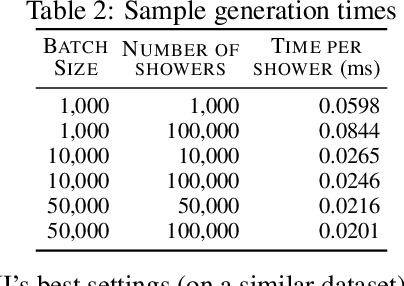
We present the results of the "Fast Calorimeter Simulation Challenge 2022" - the CaloChallenge. We study state-of-the-art generative models on four calorimeter shower datasets of increasing dimensionality, ranging from a few hundred voxels to a few tens of thousand voxels. The 31 individual submissions span a wide range of current popular generative architectures, including Variational AutoEncoders (VAEs), Generative Adversarial Networks (GANs), Normalizing Flows, Diffusion models, and models based on Conditional Flow Matching. We compare all submissions in terms of quality of generated calorimeter showers, as well as shower generation time and model size. To assess the quality we use a broad range of different metrics including differences in 1-dimensional histograms of observables, KPD/FPD scores, AUCs of binary classifiers, and the log-posterior of a multiclass classifier. The results of the CaloChallenge provide the most complete and comprehensive survey of cutting-edge approaches to calorimeter fast simulation to date. In addition, our work provides a uniquely detailed perspective on the important problem of how to evaluate generative models. As such, the results presented here should be applicable for other domains that use generative AI and require fast and faithful generation of samples in a large phase space.

The NFLikelihood: an unsupervised DNNLikelihood from Normalizing Flows

We propose the NFLikelihood, an unsupervised version, based on Normalizing Flows, of the DNNLikelihood proposed in Ref.[1]. We show, through realistic examples, how Autoregressive Flows, based on affine and rational quadratic spline bijectors, are able to learn complicated high-dimensional Likelihoods arising in High Energy Physics (HEP) analyses. We focus on a toy LHC analysis example already considered in the literature and on two Effective Field Theory fits of flavor and electroweak observables, whose samples have been obtained throught the HEPFit code. We discuss advantages and disadvantages of the unsupervised approach with respect to the supervised one and discuss possible interplays of the two.

On the curse of dimensionality for Normalizing Flows

Normalizing Flows have emerged as a powerful brand of generative models, as they not only allow for efficient sampling of complicated target distributions, but also deliver density estimation by construction. We propose here an in-depth comparison of coupling and autoregressive flows, both of the affine and rational quadratic spline type, considering four different architectures: Real-valued Non-Volume Preserving (RealNVP), Masked Autoregressive Flow (MAF), Coupling Rational Quadratic Spline (C-RQS), and Autoregressive Rational Quadratic Spline (A-RQS). We focus on different target distributions of increasing complexity with dimensionality ranging from 4 to 1000. The performances are discussed in terms of different figures of merit: the one-dimensional Wasserstein distance, the one-dimensional Kolmogorov-Smirnov test, the Frobenius norm of the difference between correlation matrices, and the training time. Our results indicate that the A-RQS algorithm stands out both in terms of accuracy and training speed. Nonetheless, all the algorithms are generally able, without much fine-tuning, to learn complex distributions with limited training data and in a reasonable time, of the order of hours on a Tesla V100 GPU. The only exception is the C-RQS, which takes significantly longer to train, and does not always provide good accuracy. All algorithms have been implemented using TensorFlow2 and TensorFlow Probability and made available on GitHub.

CaloMan: Fast generation of calorimeter showers with density estimation on learned manifolds

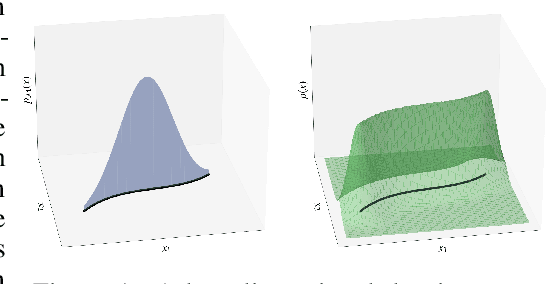
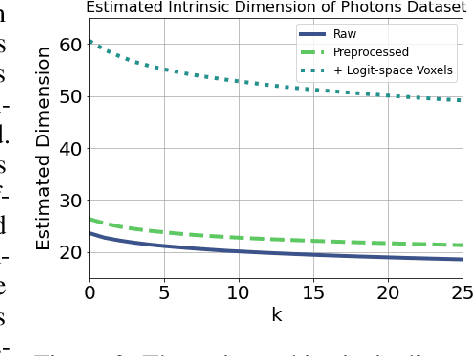
Precision measurements and new physics searches at the Large Hadron Collider require efficient simulations of particle propagation and interactions within the detectors. The most computationally expensive simulations involve calorimeter showers. Advances in deep generative modelling - particularly in the realm of high-dimensional data - have opened the possibility of generating realistic calorimeter showers orders of magnitude more quickly than physics-based simulation. However, the high-dimensional representation of showers belies the relative simplicity and structure of the underlying physical laws. This phenomenon is yet another example of the manifold hypothesis from machine learning, which states that high-dimensional data is supported on low-dimensional manifolds. We thus propose modelling calorimeter showers first by learning their manifold structure, and then estimating the density of data across this manifold. Learning manifold structure reduces the dimensionality of the data, which enables fast training and generation when compared with competing methods.

Testing the boundaries: Normalizing Flows for higher dimensional data sets

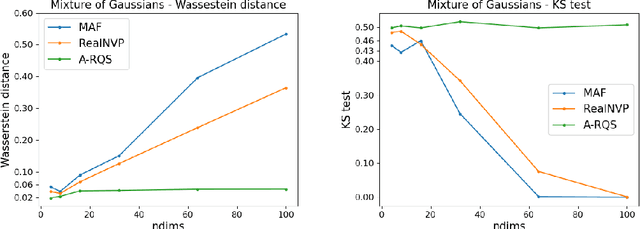
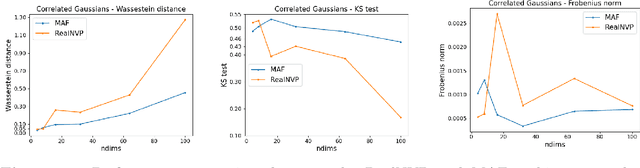
Normalizing Flows (NFs) are emerging as a powerful class of generative models, as they not only allow for efficient sampling, but also deliver, by construction, density estimation. They are of great potential usage in High Energy Physics (HEP), where complex high dimensional data and probability distributions are everyday's meal. However, in order to fully leverage the potential of NFs it is crucial to explore their robustness as data dimensionality increases. Thus, in this contribution, we discuss the performances of some of the most popular types of NFs on the market, on some toy data sets with increasing number of dimensions.