Textual Bayes: Quantifying Uncertainty in LLM-Based Systems

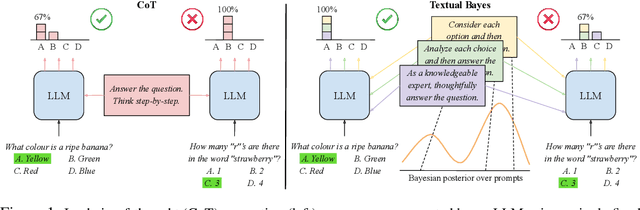
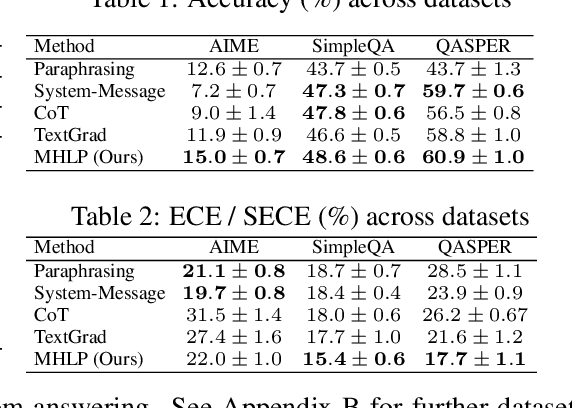
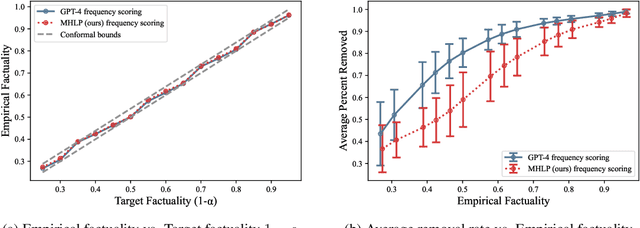
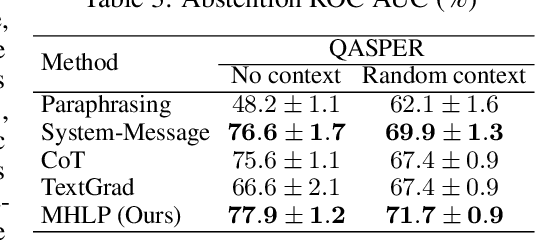
Although large language models (LLMs) are becoming increasingly capable of solving challenging real-world tasks, accurately quantifying their uncertainty remains a critical open problem, which limits their applicability in high-stakes domains. This challenge is further compounded by the closed-source, black-box nature of many state-of-the-art LLMs. Moreover, LLM-based systems can be highly sensitive to the prompts that bind them together, which often require significant manual tuning (i.e., prompt engineering). In this work, we address these challenges by viewing LLM-based systems through a Bayesian lens. We interpret prompts as textual parameters in a statistical model, allowing us to use a small training dataset to perform Bayesian inference over these prompts. This novel perspective enables principled uncertainty quantification over both the model's textual parameters and its downstream predictions, while also incorporating prior beliefs about these parameters expressed in free-form text. To perform Bayesian inference, a difficult problem even for well-studied data modalities, we introduce Metropolis-Hastings through LLM Proposals (MHLP), a novel Markov chain Monte Carlo (MCMC) algorithm that combines prompt optimization techniques with standard MCMC methods. MHLP is a turnkey modification to existing LLM pipelines, including those that rely exclusively on closed-source models. Empirically, we demonstrate that our method yields improvements in both predictive accuracy and uncertainty quantification (UQ) on a range of LLM benchmarks and UQ tasks. More broadly, our work demonstrates a viable path for incorporating methods from the rich Bayesian literature into the era of LLMs, paving the way for more reliable and calibrated LLM-based systems.

Inconsistencies In Consistency Models: Better ODE Solving Does Not Imply Better Samples

Although diffusion models can generate remarkably high-quality samples, they are intrinsically bottlenecked by their expensive iterative sampling procedure. Consistency models (CMs) have recently emerged as a promising diffusion model distillation method, reducing the cost of sampling by generating high-fidelity samples in just a few iterations. Consistency model distillation aims to solve the probability flow ordinary differential equation (ODE) defined by an existing diffusion model. CMs are not directly trained to minimize error against an ODE solver, rather they use a more computationally tractable objective. As a way to study how effectively CMs solve the probability flow ODE, and the effect that any induced error has on the quality of generated samples, we introduce Direct CMs, which \textit{directly} minimize this error. Intriguingly, we find that Direct CMs reduce the ODE solving error compared to CMs but also result in significantly worse sample quality, calling into question why exactly CMs work well in the first place. Full code is available at: https://github.com/layer6ai-labs/direct-cms.

A Geometric Framework for Understanding Memorization in Generative Models

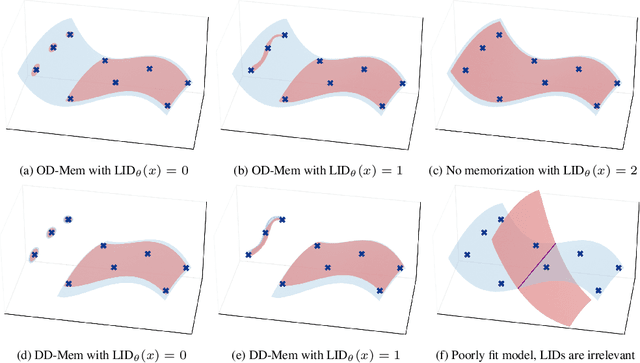
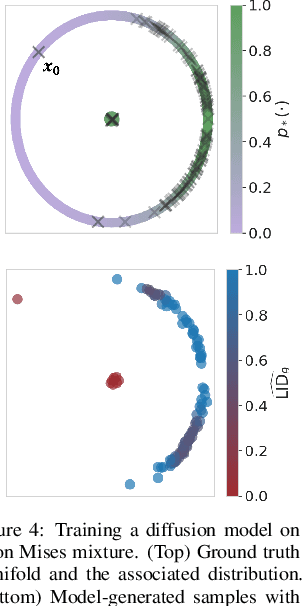
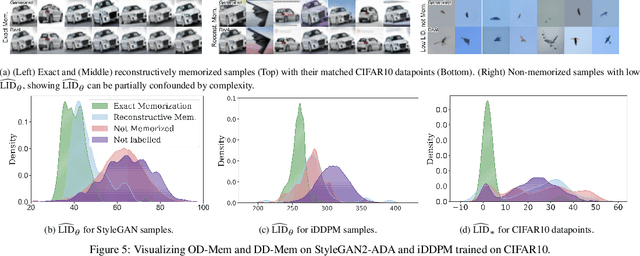
As deep generative models have progressed, recent work has shown them to be capable of memorizing and reproducing training datapoints when deployed. These findings call into question the usability of generative models, especially in light of the legal and privacy risks brought about by memorization. To better understand this phenomenon, we propose the manifold memorization hypothesis (MMH), a geometric framework which leverages the manifold hypothesis into a clear language in which to reason about memorization. We propose to analyze memorization in terms of the relationship between the dimensionalities of $(i)$ the ground truth data manifold and $(ii)$ the manifold learned by the model. This framework provides a formal standard for "how memorized" a datapoint is and systematically categorizes memorized data into two types: memorization driven by overfitting and memorization driven by the underlying data distribution. By analyzing prior work in the context of the MMH, we explain and unify assorted observations in the literature. We empirically validate the MMH using synthetic data and image datasets up to the scale of Stable Diffusion, developing new tools for detecting and preventing generation of memorized samples in the process.

CaloChallenge 2022: A Community Challenge for Fast Calorimeter Simulation

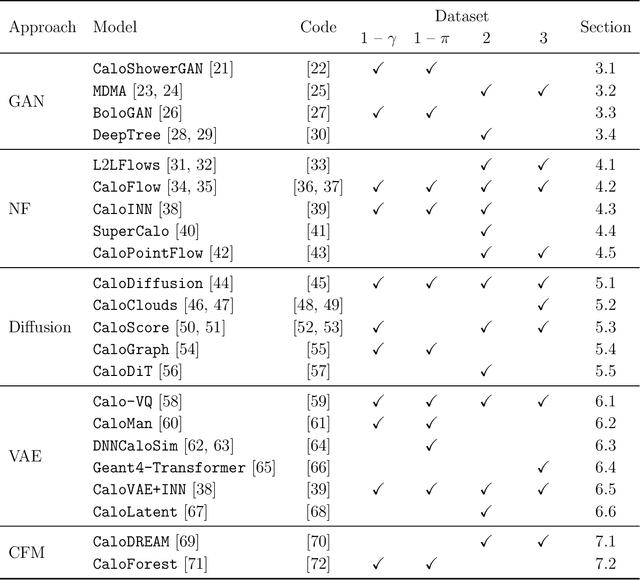
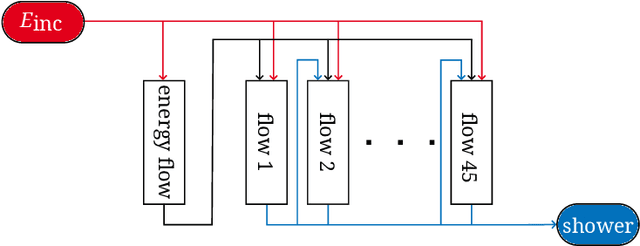
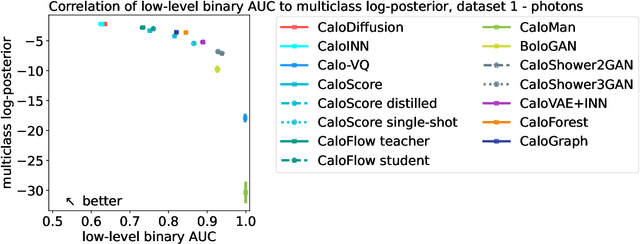
We present the results of the "Fast Calorimeter Simulation Challenge 2022" - the CaloChallenge. We study state-of-the-art generative models on four calorimeter shower datasets of increasing dimensionality, ranging from a few hundred voxels to a few tens of thousand voxels. The 31 individual submissions span a wide range of current popular generative architectures, including Variational AutoEncoders (VAEs), Generative Adversarial Networks (GANs), Normalizing Flows, Diffusion models, and models based on Conditional Flow Matching. We compare all submissions in terms of quality of generated calorimeter showers, as well as shower generation time and model size. To assess the quality we use a broad range of different metrics including differences in 1-dimensional histograms of observables, KPD/FPD scores, AUCs of binary classifiers, and the log-posterior of a multiclass classifier. The results of the CaloChallenge provide the most complete and comprehensive survey of cutting-edge approaches to calorimeter fast simulation to date. In addition, our work provides a uniquely detailed perspective on the important problem of how to evaluate generative models. As such, the results presented here should be applicable for other domains that use generative AI and require fast and faithful generation of samples in a large phase space.

A Geometric View of Data Complexity: Efficient Local Intrinsic Dimension Estimation with Diffusion Models

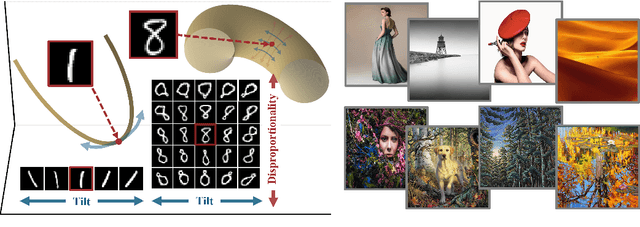
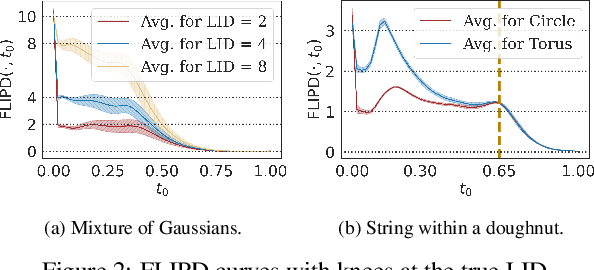
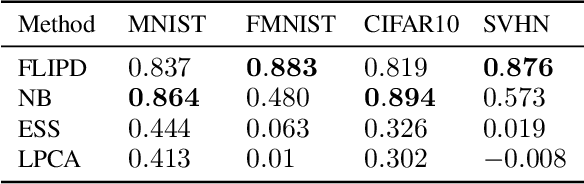
High-dimensional data commonly lies on low-dimensional submanifolds, and estimating the local intrinsic dimension (LID) of a datum -- i.e. the dimension of the submanifold it belongs to -- is a longstanding problem. LID can be understood as the number of local factors of variation: the more factors of variation a datum has, the more complex it tends to be. Estimating this quantity has proven useful in contexts ranging from generalization in neural networks to detection of out-of-distribution data, adversarial examples, and AI-generated text. The recent successes of deep generative models present an opportunity to leverage them for LID estimation, but current methods based on generative models produce inaccurate estimates, require more than a single pre-trained model, are computationally intensive, or do not exploit the best available deep generative models, i.e. diffusion models (DMs). In this work, we show that the Fokker-Planck equation associated with a DM can provide a LID estimator which addresses all the aforementioned deficiencies. Our estimator, called FLIPD, is compatible with all popular DMs, and outperforms existing baselines on LID estimation benchmarks. We also apply FLIPD on natural images where the true LID is unknown. Compared to competing estimators, FLIPD exhibits a higher correlation with non-LID measures of complexity, better matches a qualitative assessment of complexity, and is the only estimator to remain tractable with high-resolution images at the scale of Stable Diffusion.

Deep Generative Models through the Lens of the Manifold Hypothesis: A Survey and New Connections

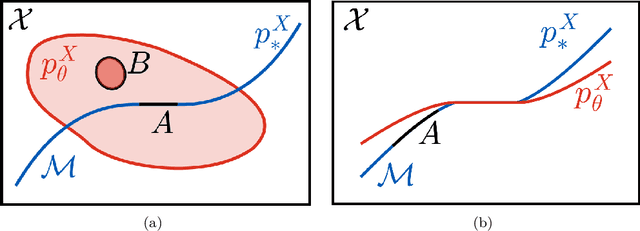
In recent years there has been increased interest in understanding the interplay between deep generative models (DGMs) and the manifold hypothesis. Research in this area focuses on understanding the reasons why commonly-used DGMs succeed or fail at learning distributions supported on unknown low-dimensional manifolds, as well as developing new models explicitly designed to account for manifold-supported data. This manifold lens provides both clarity as to why some DGMs (e.g. diffusion models and some generative adversarial networks) empirically surpass others (e.g. likelihood-based models such as variational autoencoders, normalizing flows, or energy-based models) at sample generation, and guidance for devising more performant DGMs. We carry out the first survey of DGMs viewed through this lens, making two novel contributions along the way. First, we formally establish that numerical instability of high-dimensional likelihoods is unavoidable when modelling low-dimensional data. We then show that DGMs on learned representations of autoencoders can be interpreted as approximately minimizing Wasserstein distance: this result, which applies to latent diffusion models, helps justify their outstanding empirical results. The manifold lens provides a rich perspective from which to understand DGMs, which we aim to make more accessible and widespread.

A Geometric Explanation of the Likelihood OOD Detection Paradox

Likelihood-based deep generative models (DGMs) commonly exhibit a puzzling behaviour: when trained on a relatively complex dataset, they assign higher likelihood values to out-of-distribution (OOD) data from simpler sources. Adding to the mystery, OOD samples are never generated by these DGMs despite having higher likelihoods. This two-pronged paradox has yet to be conclusively explained, making likelihood-based OOD detection unreliable. Our primary observation is that high-likelihood regions will not be generated if they contain minimal probability mass. We demonstrate how this seeming contradiction of large densities yet low probability mass can occur around data confined to low-dimensional manifolds. We also show that this scenario can be identified through local intrinsic dimension (LID) estimation, and propose a method for OOD detection which pairs the likelihoods and LID estimates obtained from a pre-trained DGM. Our method can be applied to normalizing flows and score-based diffusion models, and obtains results which match or surpass state-of-the-art OOD detection benchmarks using the same DGM backbones. Our code is available at https://github.com/layer6ai-labs/dgm_ood_detection.

Exposing flaws of generative model evaluation metrics and their unfair treatment of diffusion models

We systematically study a wide variety of image-based generative models spanning semantically-diverse datasets to understand and improve the feature extractors and metrics used to evaluate them. Using best practices in psychophysics, we measure human perception of image realism for generated samples by conducting the largest experiment evaluating generative models to date, and find that no existing metric strongly correlates with human evaluations. Comparing to 16 modern metrics for evaluating the overall performance, fidelity, diversity, and memorization of generative models, we find that the state-of-the-art perceptual realism of diffusion models as judged by humans is not reflected in commonly reported metrics such as FID. This discrepancy is not explained by diversity in generated samples, though one cause is over-reliance on Inception-V3. We address these flaws through a study of alternative self-supervised feature extractors, find that the semantic information encoded by individual networks strongly depends on their training procedure, and show that DINOv2-ViT-L/14 allows for much richer evaluation of generative models. Next, we investigate data memorization, and find that generative models do memorize training examples on simple, smaller datasets like CIFAR10, but not necessarily on more complex datasets like ImageNet. However, our experiments show that current metrics do not properly detect memorization; none in the literature is able to separate memorization from other phenomena such as underfitting or mode shrinkage. To facilitate further development of generative models and their evaluation we release all generated image datasets, human evaluation data, and a modular library to compute 16 common metrics for 8 different encoders at https://github.com/layer6ai-labs/dgm-eval.

Denoising Deep Generative Models

Likelihood-based deep generative models have recently been shown to exhibit pathological behaviour under the manifold hypothesis as a consequence of using high-dimensional densities to model data with low-dimensional structure. In this paper we propose two methodologies aimed at addressing this problem. Both are based on adding Gaussian noise to the data to remove the dimensionality mismatch during training, and both provide a denoising mechanism whose goal is to sample from the model as though no noise had been added to the data. Our first approach is based on Tweedie's formula, and the second on models which take the variance of added noise as a conditional input. We show that surprisingly, while well motivated, these approaches only sporadically improve performance over not adding noise, and that other methods of addressing the dimensionality mismatch are more empirically adequate.

CaloMan: Fast generation of calorimeter showers with density estimation on learned manifolds

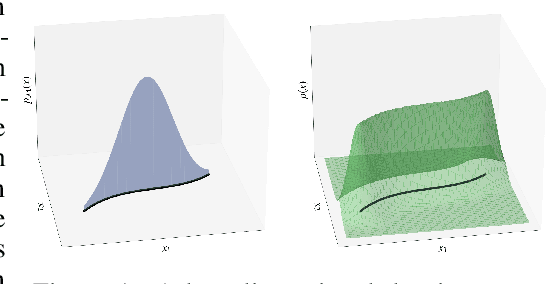
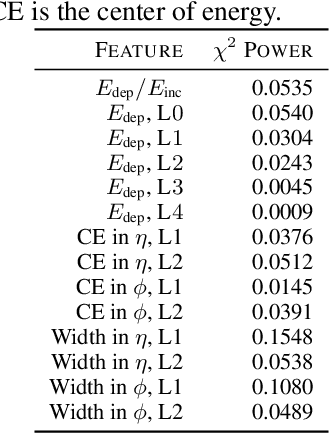
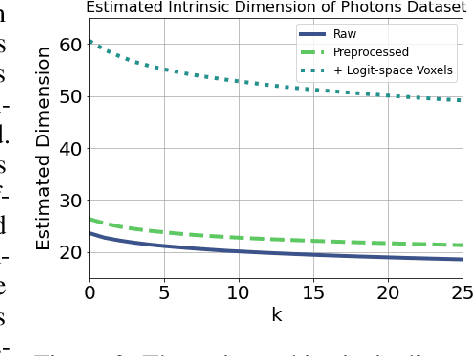
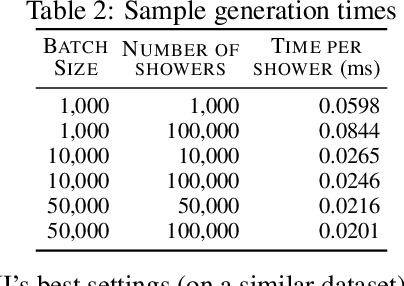
Precision measurements and new physics searches at the Large Hadron Collider require efficient simulations of particle propagation and interactions within the detectors. The most computationally expensive simulations involve calorimeter showers. Advances in deep generative modelling - particularly in the realm of high-dimensional data - have opened the possibility of generating realistic calorimeter showers orders of magnitude more quickly than physics-based simulation. However, the high-dimensional representation of showers belies the relative simplicity and structure of the underlying physical laws. This phenomenon is yet another example of the manifold hypothesis from machine learning, which states that high-dimensional data is supported on low-dimensional manifolds. We thus propose modelling calorimeter showers first by learning their manifold structure, and then estimating the density of data across this manifold. Learning manifold structure reduces the dimensionality of the data, which enables fast training and generation when compared with competing methods.