CaloChallenge 2022: A Community Challenge for Fast Calorimeter Simulation

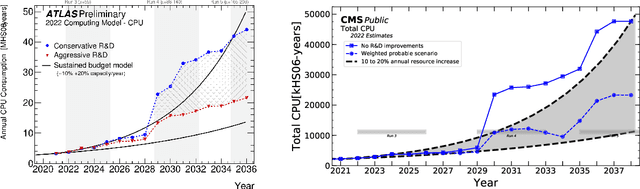
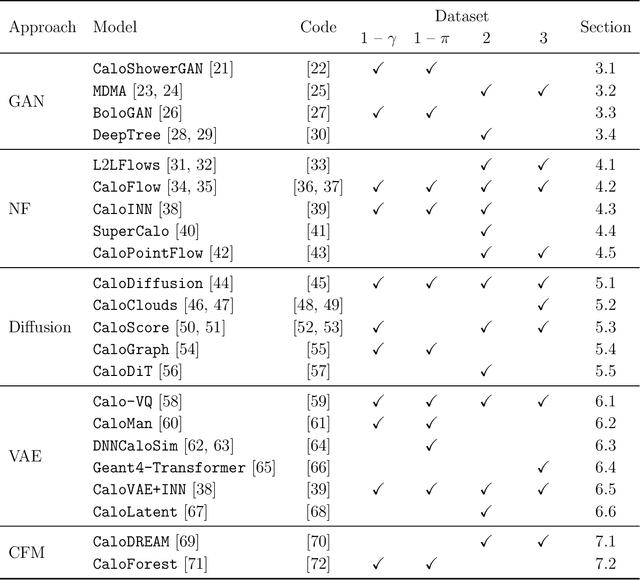
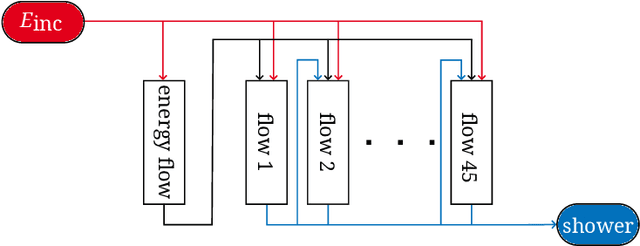
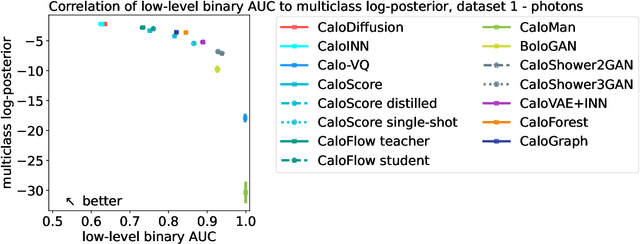
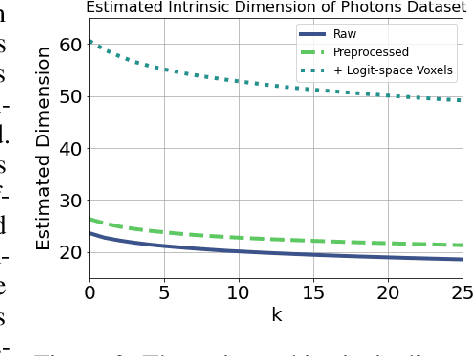
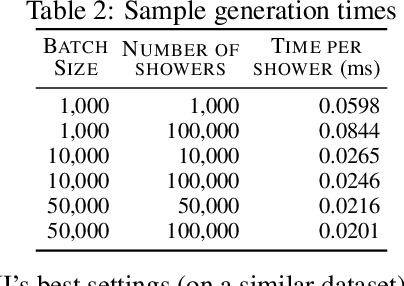
We present the results of the "Fast Calorimeter Simulation Challenge 2022" - the CaloChallenge. We study state-of-the-art generative models on four calorimeter shower datasets of increasing dimensionality, ranging from a few hundred voxels to a few tens of thousand voxels. The 31 individual submissions span a wide range of current popular generative architectures, including Variational AutoEncoders (VAEs), Generative Adversarial Networks (GANs), Normalizing Flows, Diffusion models, and models based on Conditional Flow Matching. We compare all submissions in terms of quality of generated calorimeter showers, as well as shower generation time and model size. To assess the quality we use a broad range of different metrics including differences in 1-dimensional histograms of observables, KPD/FPD scores, AUCs of binary classifiers, and the log-posterior of a multiclass classifier. The results of the CaloChallenge provide the most complete and comprehensive survey of cutting-edge approaches to calorimeter fast simulation to date. In addition, our work provides a uniquely detailed perspective on the important problem of how to evaluate generative models. As such, the results presented here should be applicable for other domains that use generative AI and require fast and faithful generation of samples in a large phase space.

Refereeing the Referees: Evaluating Two-Sample Tests for Validating Generators in Precision Sciences

We propose a robust methodology to evaluate the performance and computational efficiency of non-parametric two-sample tests, specifically designed for high-dimensional generative models in scientific applications such as in particle physics. The study focuses on tests built from univariate integral probability measures: the sliced Wasserstein distance and the mean of the Kolmogorov-Smirnov statistics, already discussed in the literature, and the novel sliced Kolmogorov-Smirnov statistic. These metrics can be evaluated in parallel, allowing for fast and reliable estimates of their distribution under the null hypothesis. We also compare these metrics with the recently proposed unbiased Fr\'echet Gaussian Distance and the unbiased quadratic Maximum Mean Discrepancy, computed with a quartic polynomial kernel. We evaluate the proposed tests on various distributions, focusing on their sensitivity to deformations parameterized by a single parameter $\epsilon$. Our experiments include correlated Gaussians and mixtures of Gaussians in 5, 20, and 100 dimensions, and a particle physics dataset of gluon jets from the JetNet dataset, considering both jet- and particle-level features. Our results demonstrate that one-dimensional-based tests provide a level of sensitivity comparable to other multivariate metrics, but with significantly lower computational cost, making them ideal for evaluating generative models in high-dimensional settings. This methodology offers an efficient, standardized tool for model comparison and can serve as a benchmark for more advanced tests, including machine-learning-based approaches.

Multiple testing for signal-agnostic searches of new physics with machine learning

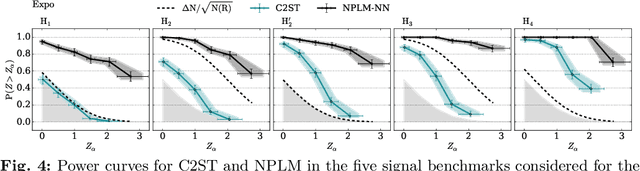
In this work, we address the question of how to enhance signal-agnostic searches by leveraging multiple testing strategies. Specifically, we consider hypothesis tests relying on machine learning, where model selection can introduce a bias towards specific families of new physics signals. We show that it is beneficial to combine different tests, characterised by distinct choices of hyperparameters, and that performances comparable to the best available test are generally achieved while providing a more uniform response to various types of anomalies. Focusing on the New Physics Learning Machine, a methodology to perform a signal-agnostic likelihood-ratio test, we explore a number of approaches to multiple testing, such as combining p-values and aggregating test statistics.

Goodness of fit by Neyman-Pearson testing

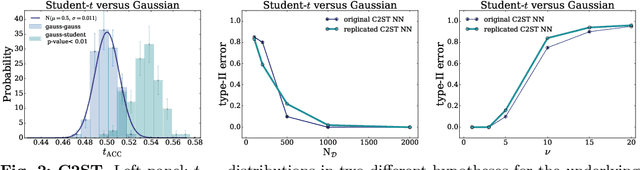
The Neyman-Pearson strategy for hypothesis testing can be employed for goodness of fit if the alternative hypothesis $\rm H_1$ is generic enough not to introduce a significant bias while at the same time avoiding overfitting. A practical implementation of this idea (dubbed NPLM) has been developed in the context of high energy physics, targeting the detection in collider data of new physical effects not foreseen by the Standard Model. In this paper we initiate a comparison of this methodology with other approaches to goodness of fit, and in particular with classifier-based strategies that share strong similarities with NPLM. NPLM emerges from our comparison as more sensitive to small departures of the data from the expected distribution and not biased towards detecting specific types of anomalies while being blind to others. These features make it more suited for agnostic searches for new physics at collider experiments. Its deployment in other contexts should be investigated.

Fast kernel methods for Data Quality Monitoring as a goodness-of-fit test

We here propose a machine learning approach for monitoring particle detectors in real-time. The goal is to assess the compatibility of incoming experimental data with a reference dataset, characterising the data behaviour under normal circumstances, via a likelihood-ratio hypothesis test. The model is based on a modern implementation of kernel methods, nonparametric algorithms that can learn any continuous function given enough data. The resulting approach is efficient and agnostic to the type of anomaly that may be present in the data. Our study demonstrates the effectiveness of this strategy on multivariate data from drift tube chamber muon detectors.

On the curse of dimensionality for Normalizing Flows

Normalizing Flows have emerged as a powerful brand of generative models, as they not only allow for efficient sampling of complicated target distributions, but also deliver density estimation by construction. We propose here an in-depth comparison of coupling and autoregressive flows, both of the affine and rational quadratic spline type, considering four different architectures: Real-valued Non-Volume Preserving (RealNVP), Masked Autoregressive Flow (MAF), Coupling Rational Quadratic Spline (C-RQS), and Autoregressive Rational Quadratic Spline (A-RQS). We focus on different target distributions of increasing complexity with dimensionality ranging from 4 to 1000. The performances are discussed in terms of different figures of merit: the one-dimensional Wasserstein distance, the one-dimensional Kolmogorov-Smirnov test, the Frobenius norm of the difference between correlation matrices, and the training time. Our results indicate that the A-RQS algorithm stands out both in terms of accuracy and training speed. Nonetheless, all the algorithms are generally able, without much fine-tuning, to learn complex distributions with limited training data and in a reasonable time, of the order of hours on a Tesla V100 GPU. The only exception is the C-RQS, which takes significantly longer to train, and does not always provide good accuracy. All algorithms have been implemented using TensorFlow2 and TensorFlow Probability and made available on GitHub.

CaloMan: Fast generation of calorimeter showers with density estimation on learned manifolds

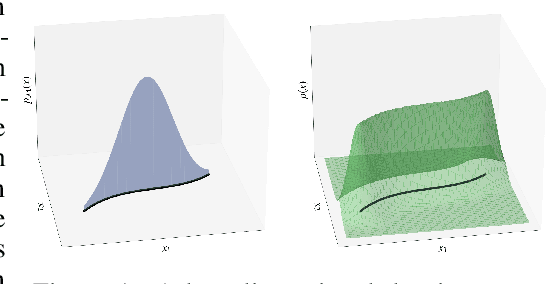
Precision measurements and new physics searches at the Large Hadron Collider require efficient simulations of particle propagation and interactions within the detectors. The most computationally expensive simulations involve calorimeter showers. Advances in deep generative modelling - particularly in the realm of high-dimensional data - have opened the possibility of generating realistic calorimeter showers orders of magnitude more quickly than physics-based simulation. However, the high-dimensional representation of showers belies the relative simplicity and structure of the underlying physical laws. This phenomenon is yet another example of the manifold hypothesis from machine learning, which states that high-dimensional data is supported on low-dimensional manifolds. We thus propose modelling calorimeter showers first by learning their manifold structure, and then estimating the density of data across this manifold. Learning manifold structure reduces the dimensionality of the data, which enables fast training and generation when compared with competing methods.

Efficient Unsupervised Learning for Plankton Images

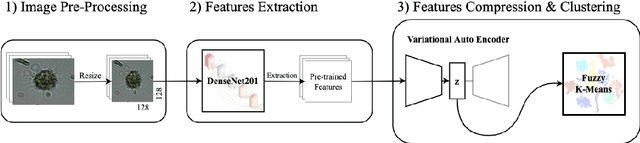
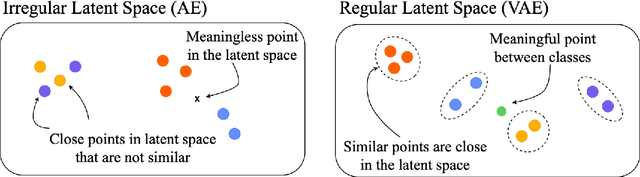
Monitoring plankton populations in situ is fundamental to preserve the aquatic ecosystem. Plankton microorganisms are in fact susceptible of minor environmental perturbations, that can reflect into consequent morphological and dynamical modifications. Nowadays, the availability of advanced automatic or semi-automatic acquisition systems has been allowing the production of an increasingly large amount of plankton image data. The adoption of machine learning algorithms to classify such data may be affected by the significant cost of manual annotation, due to both the huge quantity of acquired data and the numerosity of plankton species. To address these challenges, we propose an efficient unsupervised learning pipeline to provide accurate classification of plankton microorganisms. We build a set of image descriptors exploiting a two-step procedure. First, a Variational Autoencoder (VAE) is trained on features extracted by a pre-trained neural network. We then use the learnt latent space as image descriptor for clustering. We compare our method with state-of-the-art unsupervised approaches, where a set of pre-defined hand-crafted features is used for clustering of plankton images. The proposed pipeline outperforms the benchmark algorithms for all the plankton datasets included in our analysis, providing better image embedding properties.

Learning new physics efficiently with nonparametric methods

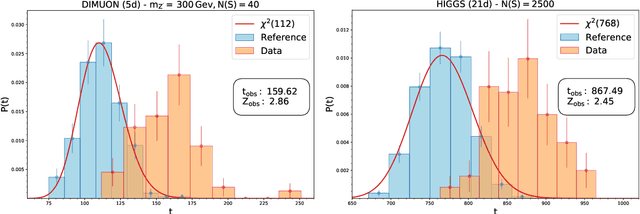
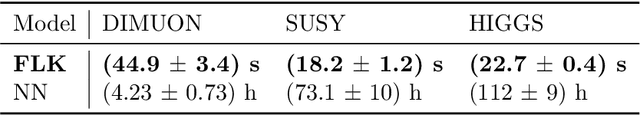
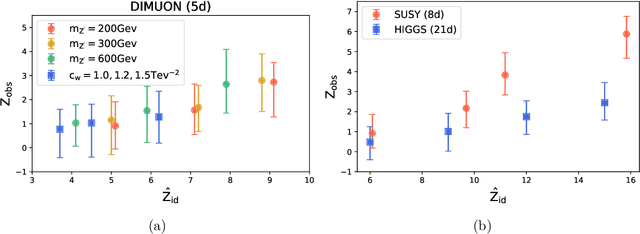
We present a machine learning approach for model-independent new physics searches. The corresponding algorithm is powered by recent large-scale implementations of kernel methods, nonparametric learning algorithms that can approximate any continuous function given enough data. Based on the original proposal by D'Agnolo and Wulzer (arXiv:1806.02350), the model evaluates the compatibility between experimental data and a reference model, by implementing a hypothesis testing procedure based on the likelihood ratio. Model-independence is enforced by avoiding any prior assumption about the presence or shape of new physics components in the measurements. We show that our approach has dramatic advantages compared to neural network implementations in terms of training times and computational resources, while maintaining comparable performances. In particular, we conduct our tests on higher dimensional datasets, a step forward with respect to previous studies.